数据结构之线性表（一）

本文主要是线性表的顺序存储结构和链式存储结构的实现和代码。

线性表的定义

线性表:零个或多个数据元素的有限序列

序列说明元素之间是有顺序的,若元素存在多个,则第一元素无前驱,最后一个元素无后继,其他元素都有且只有一个前驱和后继。有限说明元素的个数是有限的,所有在计算机中处理的数据对象都是有限的。另外在线性表的定义中，只有相同的数据类型。比如大学占位置，有一个同学拿着水杯占了三个位置，这其实并不能算线性表的定义，因为水杯并不是人。在比较复杂的线性表中，一个数据元素可以由若干个数据项组成，比如学生信息，一位同学的信息可以包括学号，姓名，年龄，性别，家庭地址等等，我们可以按照学号来划分，因为学号是有序并且有首项和末项，中间的每项都有前驱和后驱，如下图。

我们将线性表定义为（a1....ai-1,ai,ai+1....an）,则表中ai的前驱为ai-1，ai的后驱为ai-1。ai有且只有一个前驱，且只有一个后驱。所以线性表的个数n（n≥0）定义为线性表的长度，当n=0时，称为空表。

在非空线性表中确定一个数据元素的位置，a1为第一个元素，an为最后一个元素。ai是第i个元素，称i为数据元素ai在线性表中的位置。

线性表的存储结构

线性表的两种物理存储结构：顺序存储结构和链式存储结构

• 顺序存储结构：

线性表的顺序存储结构，指的是一段地址连续的存储单元依次存储线性表的数据元素。

顺序存储结构就是在内存中找了块地方，然后把这一块地址都给占用了，然后把相同数据类型的数据元素依次存在这块空地。我们可以通过一维数组来实现顺序存储结构，即把第一个数据元素存到数组下标为0的位置中，接着把相邻的元素存储的在数组中相邻的位置。我们按照线性表的最大存储容量，建立一个数组，数组的长度就是线性表的最大存储容量。在任意时刻线性表的长度要小于数组的长度。

数组的下标是从0开始的，而线性表的下标从1开始的，所以线性表第i个元素是存储的数组中下标为i-1的位置。

如上图所示，当每个元素都是占据c个存储空间，那么在第i个元素和第i+1个元素存在这么一种关系（LOC表示存储位置的函数）即：LOC(a i+!) = LOC(a i) + c,那么第i个元素在内存中的位置可以有a1推导出即：LOC(a i)=LOC(a 1)+(i -1)*c

• 顺序结构的代码实现

/**
 * 
 * @author Accper
 * 
 */
public class SqList implements IList {
    // 线性表存储空间
    private Object[] listElem;
    // 线性表的当前长度
    private int curLen;

    // 顺序表类的构造函数，构造一个存储空间容量为maxSize的线性表
    public SqList(int maxSize) {
        // TODO Auto-generated constructor stub
        curLen = 0;
        listElem = new Object[maxSize];
    }

    // 将一个已经存在的线性表置成空表
    public void clear() {
        // TODO Auto-generated method stub
        // 置顺序表的当前长度为0
        curLen = 0;
    }

    // 判断线性表中的数据元素的个数是否为0，若为0则返回true，否则返回false
    public boolean isEmpty() {
        // TODO Auto-generated method stub
        return curLen == 0;
    }

    // 求线性表中的数据元素的个数并返回其值
    public int length() {
        // TODO Auto-generated method stub
        // 返回顺序表的当前长度
        return curLen;
    }

    // 读取到线性表中的第i个数据元素并由函数返回其值，其中i的取值范围为0≤i≤length()-1，若i不在此范围则抛出异常
    public Object get(int i) {
        // TODO Auto-generated method stub
        if (i < 0 || i >= curLen) {
            throw new RuntimeException("第" + i + "个元素不存在");
        }
        return listElem[i];
    }

    // 在线性表的第i个数据元素之前插入一个值位x的数据元素
    public void insert(int i, Object x) {
        // TODO Auto-generated method stub
        // 判断表是否满了
        if (curLen == listElem.length) {
            throw new RuntimeException("存储空间已经满了，无法插入新的元素");
        }
        // 插入的位置不合法
        if (i < 0 || i > curLen) {
            throw new RuntimeException("插入的位置不合法");
        }
        // 必须要从最后一个元素开始依次逐个后移动，直到第i个数据元素移动完毕为止。
        for (int j = curLen; j > i; j--) {
            listElem[j] = listElem[j - 1];
        }
        listElem[i] = x;
        curLen++;
    }

    public void remove(int i) {
        // TODO Auto-generated method stub
        if (i < 0 || i > curLen - 1) {
            throw new RuntimeException("删除的位置不合法");
        }
        for (int j = i; j < curLen; j++) {
            listElem[j] = listElem[j+1];
        }
        curLen--;
    }

    // 返回线性表中首次出现指定的数据元素的位序号，若线性表中不包含此数据元素，则返回-1
    public int indexOf(Object x) {
        // TODO Auto-generated method stub
        for (int i = 0; i < curLen; i++) {
            if (listElem[i].equals(x)) {
                return i;
            }
        }
        return -1;
    }

    // 输出线性表中的数据元素
    public void display() {
        // TODO Auto-generated method stub
        for (int i = 0; i < curLen; i++) {
            System.out.print(listElem[i] + " ");
        }
        System.out.println();
    }

    // 测试
    public static void main(String[] args) {
        SqList sqList = new SqList(10);
        sqList.insert(0, "a");
        sqList.insert(1, "z");
        sqList.insert(2, "d");
        sqList.insert(3, "m");
        sqList.insert(4, "z");
        int order = sqList.indexOf("z");
        if (order!=-1) {
            System.out.println("顺序表中第一次出现的值为z的数据元素的位置为："+order);
        }else {
            System.out.println("顺序表中不包括z元素");
        }
    }
}

我们现在来算一下顺序存储线性表的插入和删除的时间复杂度。如果插入和删除最后一个元素，因为不需要移动元素，则时间复杂度为O(1)。如果删除和插入第一个元素，则每个元素都要向前移动或者向后移动，所以时间复杂度为O(n)，所以顺序存储结构的线性表有以下优缺点：

• 链式存储结构

线性表的链式存储结构主要特点是每个结点不仅需要存储其本身的信息外，还需要存储其后继节点的存储位置。把存储数据元素信息的域叫做数据域，把存储直接后继节点信息的域称为指针域，指针域中存储的信息叫做指针或链，这两部分组成数据元素的存储映像，称之为结点。n个结点链组成的链表，即为线性表的链式存储结构。这样就说明在内存中的存储位置可以是不连续的。

 链表中第一个存储位置叫做头指针，之后每个结点都是上一个结点的后继指针指向的位置，最后一个节点指针为“空”（通常用null或“^”表示）如下图：

 有时候我们为了方便，会在单链表的第一个结点前设置一个结点，称为头结点。头结点一般不存储信息，或者存储整个链表长度等附加信息，头结点的指针域存储着指向第一个结点的指针（如下图）

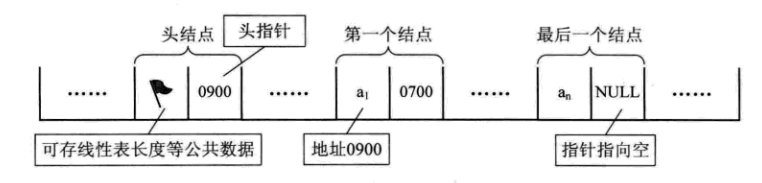
 单链表的存储示意图（如下图）

 

 带有头结点的单链表存储示意图（如下图）

 空链表结构（如下图）

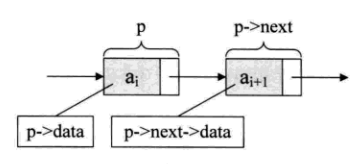
假设p是指向线性表第i个元素的指针，则ai的数据域我们用p->data来表示，p->next则是第i+1个元素的指针，也就是p->data=ai，那么p->next->data=ai+1(如下图)

 

• 链式存储结构结点实现代码

/**
 * 
 * @author Accper
 *
 */
public class Node {
    // 存放结点的值
    private Object data;
    // 后继结点的引用
    private Node next;

    // 无参数时的构造函数
    public Node() {
        // TODO Auto-generated constructor stub
        this(null, null);
    }

    // 带有一个参数时的构造函数
    public Node(Object data) {
        this(data, null);
    }

    // 带有两个参数时的构造函数
    public Node(Object data, Node next) {
        this.data = data;
        this.next = next;
    }

    public Object getData() {
        return data;
    }

    public void setData(Object data) {
        this.data = data;
    }

    public Node getNext() {
        return next;
    }

    public void setNext(Node next) {
        this.next = next;
    }
}

• 链式存储结构线性表操作类

​

/**
 * 
 * @author Accper
 *
 */
public class LinkList implements IList {
    // 单链表的头指针
    private Node head;

    // 单链表的构造函数
    public LinkList() {
        // TODO Auto-generated constructor stub
        // 初始化头结点
        head = new Node();
    }

    public LinkList(int n, boolean Order) {
        // 初始化头结点
        this();
        if (Order) {
            // 用尾插法顺序建立单链表
            create1(n);
        } else {
            // 用头插法顺序建立单链表
            create2(n);
        }
    }

    // 用头插法顺序建立单链表
    private void create2(int n) {
        // TODO Auto-generated method stub
        Scanner sc = new Scanner(System.in);
        for (int i = 0; i < n; i++) {
            insert(0, sc.next());
        }
    }

    // 用尾插法顺序建立单链表
    private void create1(int n) {
        // TODO Auto-generated method stub
        Scanner sc = new Scanner(System.in);
        for (int i = 0; i < n; i++) {
            insert(length(), sc.next());
        }
    }

    // 将一个已经存在的带头结点的单链表置成空表
    @Override
    public void clear() {
        // TODO Auto-generated method stub
        head.setData(null);
        head.setNext(null);
    }

    // 判断带头结点的单链表是否为空
    @Override
    public boolean isEmpty() {
        // TODO Auto-generated method stub
        return head.getNext() == null;
    }

    // 求带头结点的单链表的长度
    @Override
    public int length() {
        // TODO Auto-generated method stub
        // 初始化，p指向头结点，length为计数器
        Node p = head.getNext();
        int length = 0;
        // 从头结点开始向后查找，直到p为空
        while (p != null) {
            // 指向后继结点
            p = p.getNext();
            // 长度加1
            length++;
        }
        return length;
    }

    // 读取带头结点的单链表中的第i个结点
    @Override
    public Object get(int i) {
        // TODO Auto-generated method stub
        Node p = head.getNext();
        int j = 0;
        while (p != null && j < i) {
            p = p.getNext();
            j++;
        }
        // i小于0或者大于表长减1
        if (j > i || p == null) {
            throw new RuntimeException("第" + i + "个元素不存在");
        }
        return p.getData();
    }

    // 在头结点的单链表中的第i个结点之前插入一个值为x的新结点
    @Override
    public void insert(int i, Object x) {
        // TODO Auto-generated method stub
        Node p = head;
        int j = -1;
        // 寻找第i个结点的前驱
        while (p != null && j < i - 1) {
            p = p.getNext();
            j++;
        }
        if (j > i - 1 || p == null) {
            throw new RuntimeException("插入位置不合法");
        }
        Node s = new Node(x);
        // 修改链，使新结点插入到单链表中
        s.setNext(p.getNext());
        p.setNext(s);
    }

    // 删除带头结点的单链表中的第i个结点
    @Override
    public void remove(int i) {
        // TODO Auto-generated method stub
        Node p = head;
        int j = -1;
        while (p.getNext() != null && j < i - 1) {
            p = p.getNext();
            j++;
        }
        if (j > i - 1 || p.getNext() == null) {
            throw new RuntimeException("删除位置不合法");
        }
        // 修改链指针，使待删除结点从单链表中脱离
        p.setNext(p.getNext().getNext());
    }

    // 查找指定单链表中元素的位置，若在单链表中值发回该位置，如果不在单链表中则返回-1
    @Override
    public int indexOf(Object x) {
        // TODO Auto-generated method stub
        Node p = head.getNext();
        int j = 0;
        while (p != null && p.getData().equals(x)) {
            p = p.getNext();
            j++;
        }
        if (p == null) {
            return -1;
        } else {
            return j;
        }
    }

    // 输出单链表中的所有结点
    @Override
    public void display() {
        // TODO Auto-generated method stub
        // 取出带头结点的单链表中的首结点
        Node p = head.getNext();
        while (p != null) {
            // 输出结点的值
            System.out.print(p.getData() + " ");
            // 取下一个结点
            p = p.getNext();
        }
        System.out.println();
    }

    // 测试
    public static void main(String[] args) {
        int n = 10;
        LinkList L = new LinkList();
        for (int i = 0; i < n; i++) {
            L.insert(i, i);
        }
        System.out.println("请输入i的值：");
        int i = new Scanner(System.in).nextInt();
        if (0 < i && i <= n) {
            System.out.println("第" + i + "个元素的前驱是:" + L.get(i - 1));
        } else {
            System.out.println("第" + i + "个元素的直接前驱不存在");
        }
    }
}

[点击并拖拽以移动]
​

• 单链表（链表存储结构线性表）和顺序存储结构线性表的优缺点

 当线性表需要经常查找，很少删除和插入时，这时选用顺序结构线性表。当频繁插入和删除时，选用单链表。当线性表中的元素个数变化较大，也需要选用单链表结构。