二叉树定义
二叉树(Binary Tree)是n(n≥0)个结点的有限集合,该集合可以为空集称为空二叉树,或者一个根结点和两个互不相交的,分别称为根结点的左子树和右子树的二叉树组成。
如开/关,0/1,真/假,上/下,对/错等,对于这种在某个阶段都是两种可能性的情况,我们可以用树形结构来建模,而这种树就是特殊的树形结构称为二叉树。
二叉树的特点:
- 每个结点最多两棵子树,没有或一棵也行。
- 左子树和右子树是有顺序的,无法颠倒。
- 树中某个结点如果只有一棵子树,也要区分是左子树还是右子树。
二叉树五种基本形态:
- 空二叉树
- 只有一个根结点
- 根结点只有左子树
- 根结点只有右子树
- 根结点左子树和右子树都存在。
如果有三个结点组成的树,只从形态考虑只有两种,如下图,两层的树1和三层的后四种任意一种,但是二叉树要区分左右,所有就是五种形态,下图的树2,3,4,5代表不同的二叉树。

特殊二叉树种类:
- 斜树,所有结点只有左子树的二叉树称为左斜树,所有结点只有右子树的二叉树称为右斜树,统称为斜树。
- 满二叉树,所有分支结点都存在左子树和右子树,并且所有叶子都在同一层,称为满二叉树。
- 完全二叉树,对于一棵具有n个结点按照层序编号,如果编号i(1≤i≤n)的结点和同样深度的满二叉树编号为i的结点在二叉树中位置完全相同,那么称之为完全二叉树。
完全二叉树的定义:
满二叉树一定是完全二叉树,完全二叉树却不一定是满二叉树。其次完全二叉树的所有结点,与同样深度的满二叉树,它们按照层序编号相同的结点是一一对应的,并且编号不能空档。

完全二叉树特点:1.叶子结点只能出现在最下面两层。2.最下层的叶子结点一定是左部连续的。3.倒数两层,如果有叶子结点一定是在右部连续的。4.结点度为1,则只有左孩子。5.同样结点的二叉树,完全二叉树的深度最小。
二叉树的特性:



二叉树的存储结构:
顺序存储结构:
由于二叉树是一种特别的树,也是可以用顺序存储结构来实现的,二叉树的顺序存储结构就是用一维数组来存储二叉树的结点,并且结点的存储位置用数组的下标来表示逻辑关系。

将二叉树存储数组,相应的下标对于相应的位置,如下图:

对于一般的二叉树,如果对应的结点不存在,我们将数组的值设置为“^”,如下图:

一棵深度为K的右斜树,如下图,就会造成空间浪费,所以一般我们用顺序存储结构来存储完全二叉树。

二叉树链表存储结构:
因为二叉树每个结点至多有两个孩子,所以我们设置一个数据域,两个指针域是最合适的,我们称之为二叉链表。
| lchild | data | rchild |
| 指向左孩子 | 数据域 | 指向右孩子 |

二叉链表存储结构:
public static class Node{
Object data;
Node left;
Node right;
public Node(){
}
public Node(Object data){
this.data=data;
this.left=null;
this.right=null;
}
public Node(Object data,Node left,Node right){
this.data=data;
this.left=left;
this.right=right;
}
}
遍历二叉树:
二叉树的遍历是指从根结点开始,按照某种次序依次访问二叉树中的所有结点,使得每个结点仅被访问一次。
前序遍历:若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子树,在前序遍历右子树,如下图,访问顺序为ABDGHCEIF

中序遍历:若二叉树为空,则空操作返回,否则从根结点开始(并不是先访问根结点),中序遍历根结点左子树,然后访问根结点,最后中序遍历根结点右子树,如下图,访问顺序GDHBAEICF

后序遍历:若二叉树为空,则空操作返回,否则从左到右先叶子后结点的顺序遍历访问左右子树,最后是根结点,如下图,访问顺序为:GHDBIEFCA

层序遍历:若二叉树为空,则空操作返回,否则从树的第一层,也就是根结点访问,从上至下逐层遍历,在同一层中,按照从左到右的顺序访问,如下图,访问顺序为:ABCDEFGHI

我们以上四种遍历方式,对于计算机就是把树中的结点变成某种意义的线性结构序列,给程序的实现带来了好处,不同的遍历方式提供了对结点依次处理的不同方式,可以在遍历中对结点进行操作。
遍历代码实现:
public class BinaryTree<T>
{
/*
* 先序创建二叉树
* 返回:根节点
*/
public TreeNode<T> creatBinaryPre(LinkedList<T> treeData)
{
TreeNode<T> root=null;
T data=treeData.removeFirst();
if (data!=null)
{
root=new TreeNode<T>(data, null, null);
root.left=creatBinaryPre(treeData);
root.right=creatBinaryPre(treeData);
}
return root;
}
/*
* 先序遍历二叉树(递归)
*/
public void PrintBinaryTreePreRecur(TreeNode<T> root)
{
if (root!=null)
{
System.out.print(root.data);
PrintBinaryTreePreRecur(root.left);
PrintBinaryTreePreRecur(root.right);
}
}
/*
* 中序遍历二叉树(递归)
*/
public void PrintBinaryTreeMidRecur(TreeNode<T> root)
{
if (root!=null)
{
PrintBinaryTreeMidRecur(root.left);
System.out.print(root.data);
PrintBinaryTreeMidRecur(root.right);
}
}
/*
* 后序遍历二叉树(递归)
*/
public void PrintBinaryTreeBacRecur(TreeNode<T> root)
{
if (root!=null)
{
PrintBinaryTreeBacRecur(root.left);
PrintBinaryTreeBacRecur(root.right);
System.out.print(root.data);
}
}
/*
* 先序遍历二叉树(非递归)
* 思路:对于任意节点T,访问这个节点并压入栈中,然后访问节点的左子树,
* 遍历完左子树后,取出栈顶的节点T,再先序遍历T的右子树
*/
public void PrintBinaryTreePreUnrecur(TreeNode<T> root)
{
TreeNode<T> p=root;//p为当前节点
LinkedList<TreeNode> stack=new LinkedList<>();
//栈不为空时,或者p不为空时循环
while(p!=null || !stack.isEmpty())
{
//当前节点不为空。访问并压入栈中。并将当前节点赋值为左儿子
if (p!=null)
{
stack.push(p);
System.out.print(p.data);
p=p.left;
}
//当前节点为空:
// 1、当p指向的左儿子时,此时栈顶元素必然是它的父节点
// 2、当p指向的右儿子时,此时栈顶元素必然是它的爷爷节点
//取出栈顶元素,赋值为right
else
{
p=stack.pop();
p=p.right;
}
}
}
/*
* 中序遍历二叉树(非递归)
*
* 思路:先将T入栈,遍历左子树;遍历完左子树返回时,栈顶元素应为T,
* 出栈,访问T->data,再中序遍历T的右子树。
*/
public void PrintBinaryTreeMidUnrecur(TreeNode<T> root)
{
TreeNode<T> p=root;//p为当前节点
LinkedList<TreeNode> stack=new LinkedList<>();
//栈不为空时,或者p不为空时循环
while(p!=null || !stack.isEmpty())
{
//当前节点不为空。压入栈中。并将当前节点赋值为左儿子
if (p!=null)
{
stack.push(p);
p=p.left;
}
//当前节点为空:
// 1、当p指向的左儿子时,此时栈顶元素必然是它的父节点
// 2、当p指向的右儿子时,此时栈顶元素必然是它的爷爷节点
//取出并访问栈顶元素,赋值为right
else
{
p=stack.pop();
System.out.print(p.data);
p=p.right;
}
}
}
/*
* 后序遍历二叉树(非递归)
*
*/
public void PrintBinaryTreeBacUnrecur(TreeNode<T> root)
{
class NodeFlag<T>
{
TreeNode<T> node;
char tag;
public NodeFlag(TreeNode<T> node, char tag) {
super();
this.node = node;
this.tag = tag;
}
}
LinkedList<NodeFlag<T>> stack=new LinkedList<>();
TreeNode<T> p=root;
NodeFlag<T> bt;
//栈不空或者p不空时循环
while(p!=null || !stack.isEmpty())
{
//遍历左子树
while(p!=null)
{
bt=new NodeFlag(p, 'L');
stack.push(bt);
p=p.left;
}
//左右子树访问完毕访问根节点
while(!stack.isEmpty() && stack.getFirst().tag=='R')
{
bt=stack.pop();
System.out.print(bt.node.data);
}
//遍历右子树
if (!stack.isEmpty())
{
bt=stack.peek();
bt.tag='R';
p=bt.node;
p=p.right;
}
}
}
/*
* 层次遍历二叉树(非递归)
*/
public void PrintBinaryTreeLayerUnrecur(TreeNode<T> root)
{
LinkedList<TreeNode> queue=new LinkedList<>();
TreeNode<T> p;
queue.push(root);
while(!queue.isEmpty())
{
p=queue.removeFirst();
System.out.print(p.data);
if (p.left!=null)
queue.addLast(p.left);
if (p.right!=null)
queue.addLast(p.right);
}
}
}
class TreeNode<T>
{
public T data;
public TreeNode<T> left;
public TreeNode<T> right;
public TreeNode(T data, TreeNode<T> left, TreeNode<T> right)
{
this.data = data;
this.left = left;
this.right = right;
}
}
推导遍历结果:
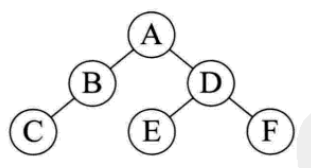
已知一棵树前序遍历为ABCDEF,中序遍历CBAEDF,请问后序遍历结果?
前序遍历第一个打印的A,说明A就是根结点的数据,中序遍历A左边有CB,右边有EDF,证明CB是A的左子树,EDF是A的右子树
前序遍历中先打印的B,再打印的C,所以B是A的左孩子,那么C就只能是B的孩子,再看中序遍历,C是在B之前打印的,说明C是B的左孩子

再看前序遍历的EDF,顺序是ABCDEF,说明D是A的右孩子,E,F是D的子孙,再看中序遍历CBAEDF,由于E在D的左侧,F在D的右侧,所以E是D的左子树,F是D的右子树
二叉树的建立:
建立二叉树利用了递归的原理
public class BinTreeTraverse2 {
private int[] array = { 1, 2, 3, 4, 5, 6, 7, 8, 9 };
private static List<Node> nodeList = null;
/**
* 内部类:节点
*
*
*/
private static class Node {
Node leftChild;
Node rightChild;
int data;
Node(int newData) {
leftChild = null;
rightChild = null;
data = newData;
}
}
public void createBinTree() {
nodeList = new LinkedList<Node>();
// 将一个数组的值依次转换为Node节点
for (int nodeIndex = 0; nodeIndex < array.length; nodeIndex++) {
nodeList.add(new Node(array[nodeIndex]));
}
// 对前lastParentIndex-1个父节点按照父节点与孩子节点的数字关系建立二叉树
for (int parentIndex = 0; parentIndex < array.length / 2 - 1; parentIndex++){
// 左孩子
nodeList.get(parentIndex).leftChild = nodeList
.get(parentIndex * 2 + 1);
// 右孩子
nodeList.get(parentIndex).rightChild = nodeList
.get(parentIndex * 2 + 2);
}
// 最后一个父节点:因为最后一个父节点可能没有右孩子,所以单独拿出来处理
int lastParentIndex = array.length / 2 - 1;
// 左孩子
nodeList.get(lastParentIndex).leftChild = nodeList
.get(lastParentIndex * 2 + 1);
// 右孩子,如果数组的长度为奇数才建立右孩子
if (array.length % 2 == 1) {
nodeList.get(lastParentIndex).rightChild = nodeList
.get(lastParentIndex * 2 + 2);
}
}
}