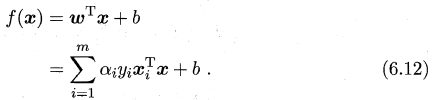机器学习读书笔记------支持向量机

     SVM是一种有监督的统计学习方法，能够最小化经验误差和最大化几何边缘，被称为最大间隔分类器，可用于分类与回归分析

一、间隔与支持向量

     给定训练样本集D={(x₁,y₁),(x₂,y₂),...,(x_m,y_m)},y_i∈{-1,+1}，分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面，将不同类别的样本分开。在众多划分超平面之间，我们需要找出一个泛化能力最强的。直观上看，我们应该找位于两类训练样本“正中间”的划分超平面，该平面对训练样本局部扰动的“容忍”性最好。换言之，这个划分超平面所产生的分类结果是最鲁棒的，对未见示例的泛化能力最强。

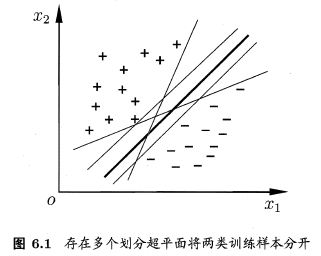
      在样本空间中，划分超平面可通过线性方程来描述：w^Tx+b=0 ,其中w=(w1;w2;...;wd)为法向量，决定了超平面的方向；b为位移项，决定了超平面与原点之间的距离。即划分超平面可被法向量w和位移b确定。并将其记为（w,b）。

     样本空间中任意点x到超平面（w,b）的距离可写为：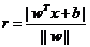

     假设超平面（w,b）能训练样本正确分类，即对于（x_i,y_i）∈D,若y_i=+1，则有w^Tx_i+b>0;若y_i=-1，则有w^Tx_i+b<0.令

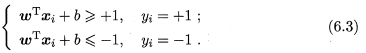
     如下图所示，距离超平面最近的这几个训练样本点使上式成立，被称为“支持向量”，两个异类支持向量到超平面的距离之和为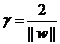，它被称为“间隔”。

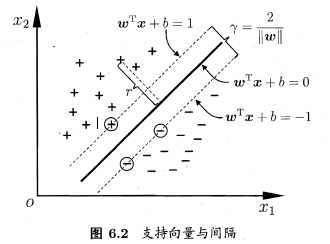
    欲找到具有“最大间隔”的划分超平面，即找到满足（6.3）的参数w和b，从而使得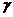最大，即

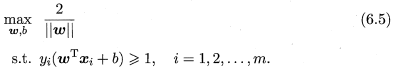
    可知，为了使间隔最大化，仅需最大化||w||^-1,则上式可改为

  此即支持向量机（SVM）的基本型。

二、对偶问题

      我们需要求解（6.6）式来得到大间隔划分超平面所对应的模型  f(x)=w^Tx+b，其中w和b是模型参数，由于式（6.6）是一个凸二次规划问题（convex quadratic programming），能直接用优化计算包求解，也可有更高效的方法。对式（6.6）使用拉格朗日乘子法可得到其“对偶问题”。对（6.6）的每条约束添加拉格朗日乘子α_i≥0，则该问题的拉格朗日函数可写为：

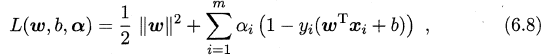
其中α=（α₁;α₂;...;α_m）.令L(w,b,α)对w和 b的偏导为零可得

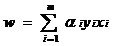 （6.9）

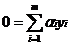          （6.10）

利用这两个式子对（6.8）式进行化简可得到式（6.6）的对偶问题

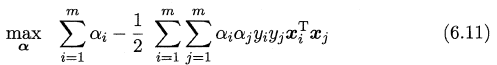
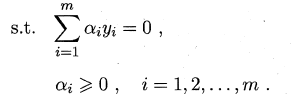
解出α求出w和b可得到模型