-
为什么要用卷积神经网络?
传统神经网络的劣势
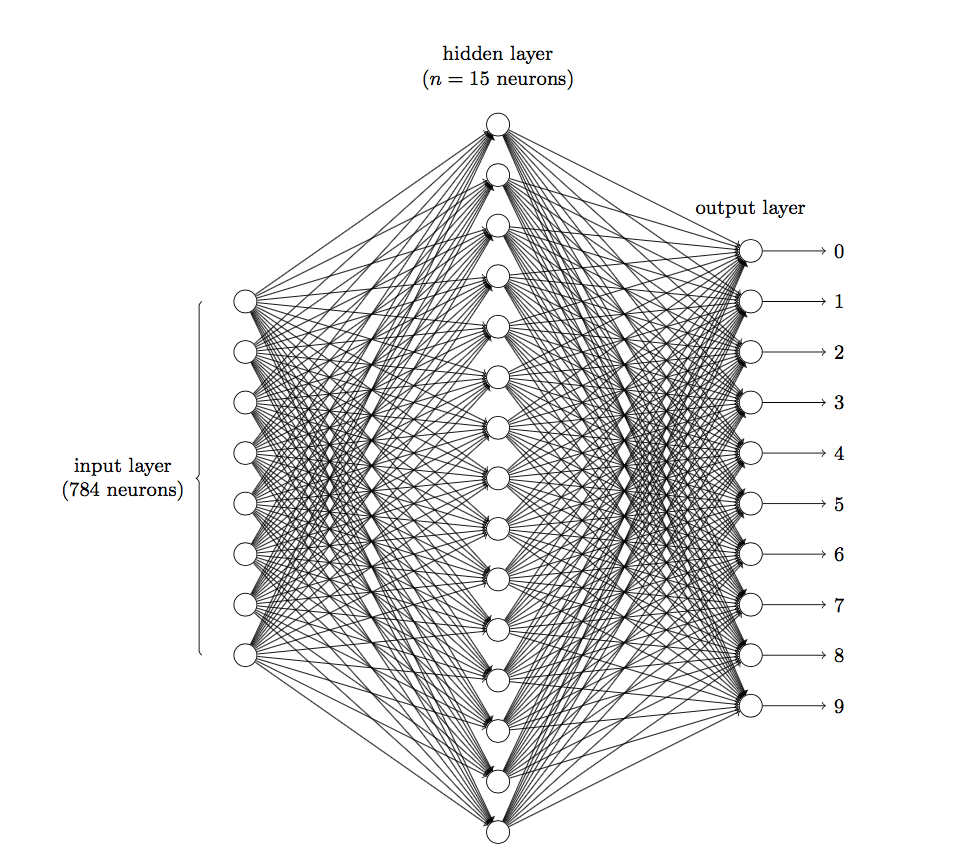
我们知道,图像是由一个个像素点构成,每个像素点有三个通道,分别代表RGB颜色,那么,如果一个图像的尺寸是(28,28,1),即代表这个图像的是一个长宽均为28,channel为1的图像(channel也叫depth,此处1代表灰色图像)。如果使用全连接的网络结构,即网络中的神经与与相邻层上的每个神经元均连接,那就意味着我们的网络有28 * 28 =784个神经元,hidden层采用了15个神经元,那么简单计算一下,我们需要的参数个数(w和b)就有:784*15*10+15+10=117625个,这个参数太多了,随便进行一次反向传播计算量都是巨大的,从计算资源和调参的角度都不建议用传统的神经网络。
卷积神经网络是什么?
三个基本层
- 卷积层(Convolutional Layer)
我们用传统的三层神经网络需要大量的参数,原因在于每个神经元都和相邻层的神经元相连接,但是思考一下,这种连接方式是必须的吗?全连接层的方式对于图像数据来说似乎显得不这么友好,因为图像本身具有“二维空间特征”,通俗点说就是局部特性。譬如我们看一张猫的图片,可能看到猫的眼镜或者嘴巴就知道这是张猫片,而不需要说每个部分都看完了才知道,啊,原来这个是猫啊。所以如果我们可以用某种方式对一张图片的某个典型特征识别,那么这张图片的类别也就知道了。这个时候就产生了卷积的概念。举个例子,现在有一个4*4的图像,我们设计两个卷积核,看看运用卷积核后图片会变成什么样。
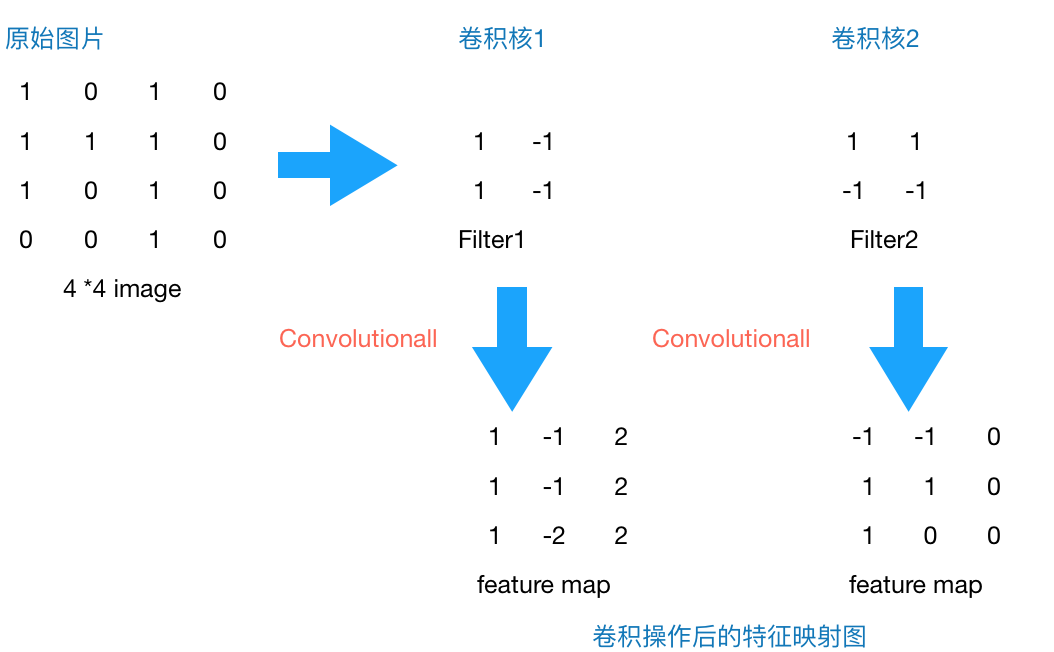
由上图可以看到,原始图片是一张灰度图片,每个位置表示的是像素值,0表示白色,1表示黑色,(0,1)区间的数值表示灰色。对于这个4*4的图像,我们采用两个2*2的卷积核来计算。设定步长为1,即每次以2*2的固定窗口往右滑动一个单位。以第一个卷积核filter1为例,计算过程如下:
feature_map1(1,1) = 1*1 + 0*(-1) + 1*1 + 1*(-1) = 1
feature_map1(1,2) = 0*1 + 1*(-1) + 1*1 + 1*(-1) = -1
```
feature_map1(3,3) = 1*1 + 0*(-1) + 1*1 + 0*(-1) = 2
可以看到这就是最简单的内积公式。feature_map1(1,1)表示在通过第一个卷积核计算完后得到的feature_map的第一行第一列的值,随着卷积核的窗口不断的滑动,我们可以计算出一个3*3的feature_map1;同理可以计算通过第二个卷积核进行卷积运算后的feature_map2,那么这一层卷积操作就完成了。feature_map尺寸计算公式:[ (原图片尺寸 -卷积核尺寸)/ 步长 ] + 1。
为什么卷积核有效?
那么问题来了,虽然我们知道了卷积核是如何计算的,但是为什么使用卷积核计算后分类效果要由于普通的神经网络呢?我们仔细来看一下上面计算的结果。通过第一个卷积核计算后的feature_map是一个三维数据,在第三列的绝对值最大,说明原始图片上对应的地方有一条垂直方向的特征,即像素数值变化较大;而通过第二个卷积核计算后,第三列的数值为0,第二行的数值绝对值最大,说明原始图片上对应的地方有一条水平方向的特征。
仔细思考一下,这个时候,我们设计的卷积核分别能够提取,或者说检测出原始图片的特定的特征。此时我们其实就可以把卷积核就理解为特征提取器啊!现在就明白了,为什么我们只需要把图片数据灌进去,设计好卷积核的尺寸、数量和滑动的步长就可以让自动提取出图片的某些特征,从而达到分类的效果啊!
注:1.此处的卷积运算是两个卷积核大小的矩阵的内积运算,不是矩阵乘法。即相同位置的数字相乘再相加求和。
2.卷积核的公式有很多,这只是最简单的一种。我们所说的卷积核在数字信号处理里也叫滤波器,那滤波器的种类就多了,均值滤波器,高斯滤波器,拉普拉斯滤波器等等,不过,不管是什么滤波器,都只是一种数学运算,无非就是计算更复杂一点。
3.每一层的卷积核大小和个数可以自己定义,不过一般情况下,根据实验得到的经验来看,会在越靠近输入层的卷积层设定少量的卷积核,越往后,卷积层设定的卷积核数目就越多。
- 池化层(Pooling Layer)
通过上一层2*2的卷积核操作后,我们将原始图像由4*4的尺寸变为了3*3的一个新的图片。池化层的主要目的是通过降采样的方式,在不影响图像质量的情况下,压缩图片,减少参数。简单来说,假设现在设定池化层采用MaxPooling,大小为2*2,步长为1,取每个窗口最大的数值重新,那么图片的尺寸就会由3*3变为2*2:(3-2)+1=2。从上例来看,会有如下变换:
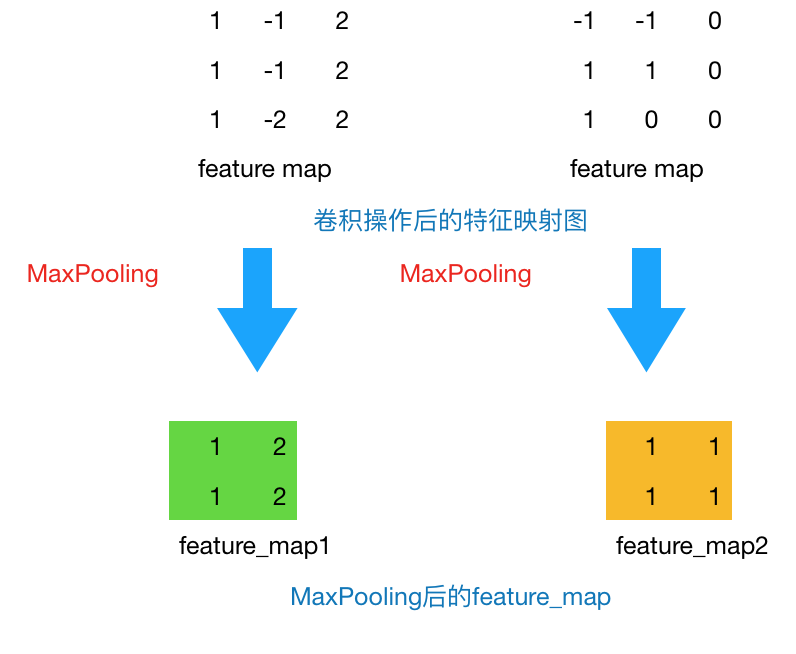
通常来说,池化方法一般有一下两种:
- MaxPooling:取滑动窗口里最大的值
- AveragePooling:取滑动窗口内所有值的平均值
为什么采用Max Pooling?
从计算方式来看,算是最简单的一种了,取max即可,但是这也引发一个思考,为什么需要Max Pooling,意义在哪里?如果我们只取最大值,那其他的值被舍弃难道就没有影响吗?不会损失这部分信息吗?如果认为这些信息是可损失的,那么是否意味着我们在进行卷积操作后仍然产生了一些不必要的冗余信息呢?
其实从上文分析卷积核为什么有效的原因来看,每一个卷积核可以看做一个特征提取器,不同的卷积核负责提取不同的特征,我们例子中设计的第一个卷积核能够提取出“垂直”方向的特征,第二个卷积核能够提取出“水平”方向的特征,那么我们对其进行Max Pooling操作后,提取出的是真正能够识别特征的数值,其余被舍弃的数值,对于我提取特定的特征并没有特别大的帮助。那么在进行后续计算使,减小了feature map的尺寸,从而减少参数,达到减小计算量,却不损失效果的情况。
不过并不是所有情况Max Pooling的效果都很好,有时候有些周边信息也会对某个特定特征的识别产生一定效果,那么这个时候舍弃这部分“不重要”的信息,就不划算了。所以具体情况得具体分析,如果加了Max Pooling后效果反而变差了。
Zero Padding
所以到现在为止,我们的图片由4*4,通过卷积层变为3*3,再通过池化层变化2*2,如果我们再添加层,那么图片岂不是会越变越小?这个时候我们就会引出“Zero Padding”(补零),它可以帮助我们保证每次经过卷积或池化输出后图片的大小不变,如,上述例子我们如果加入Zero Padding,再采用3*3的卷积核,那么变换后的图片尺寸与原图片尺寸相同,如下图所示:

通常情况下,我们希望图片做完卷积操作后保持图片大小不变,所以我们一般会选择尺寸为3*3的卷积核和1的zero padding,或者5*5的卷积核与2的zero padding,这样通过计算后,可以保留图片的原始尺寸。那么加入zero padding后的feature_map尺寸 =( width + 2 * padding_size - filter_size )/stride + 1
注:这里的width也可换成height,此处是默认正方形的卷积核,weight = height,如果两者不相等,可以分开计算,分别补零。
- Flatten层 & Fully Connected Layer
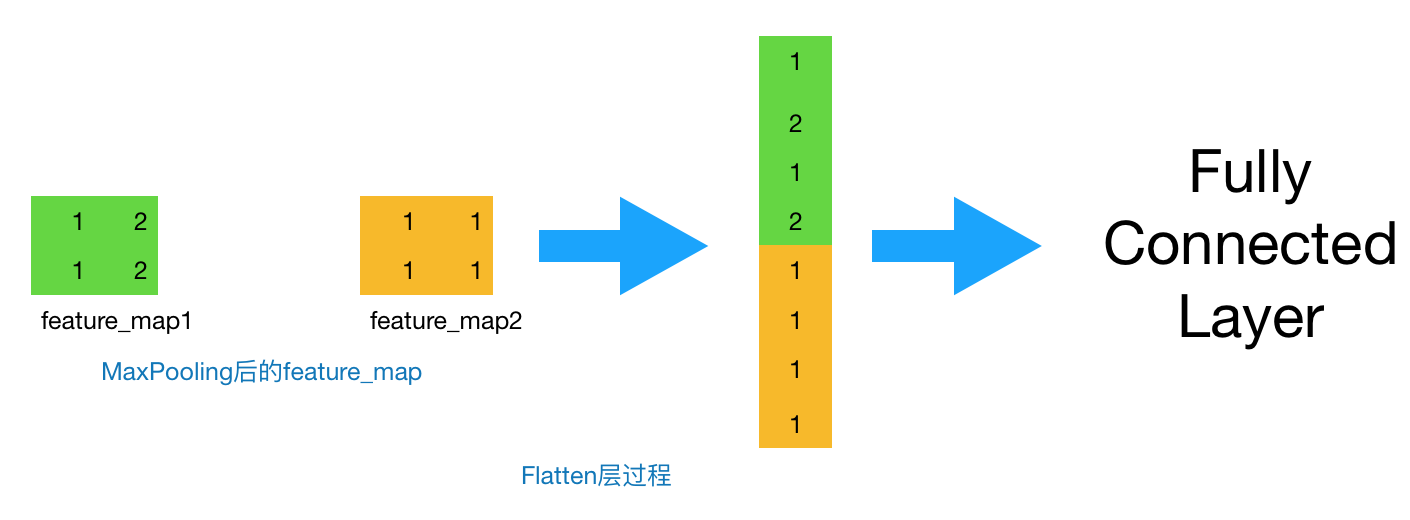
到这一步,其实我们的一个完整的“卷积部分”就算完成了,如果想要叠加层数,一般也是叠加“Conv-MaxPooing",通过不断的设计卷积核的尺寸,数量,提取更多的特征,最后识别不同类别的物体。做完Max Pooling后,我们就会把这些数据“拍平”,丢到Flatten层,然后把Flatten层的output放到full connected Layer里,采用softmax对其进行分类。
- 小结
1.卷积核的尺寸不一定非得为正方形。长方形也可以,只不过通常情况下为正方形。如果要设置为长方形,那么首先得保证这层的输出形状是整数,不能是小数。如果你的图像是边长为 28 的正方形。那么卷积层的输出就满足 [ (28 - kernel_size)/ stride ] + 1 ,这个数值得是整数才行,否则没有物理意义。譬如,你算得一个边长为 3.6 的 feature map 是没有物理意义的。 pooling 层同理。FC 层的输出形状总是满足整数,其唯一的要求就是整个训练过程中 FC 层的输入得是定长的。如果你的图像不是正方形。那么在制作数据时,可以缩放到统一大小(非正方形),再使用非正方形的 kernel_size 来使得卷积层的输出依然是整数。
2.由经验确定。通常情况下,靠近输入的卷积层,譬如第一层卷积层,会找出一些共性的特征,如手写数字识别中第一层我们设定卷积核个数为5个,一般是找出诸如"横线"、“竖线”、“斜线”等共性特征,我们称之为basic feature,经过max pooling后,在第二层卷积层,设定卷积核个数为20个,可以找出一些相对复杂的特征,如“横折”、“左半圆”、“右半圆”等特征,越往后,卷积核设定的数目越多,越能体现label的特征就越细致,就越容易分类出来,打个比方,如果你想分类出“0”的数字,你看到![]() 这个特征,能推测是什么数字呢?只有越往后,检测识别的特征越多,试过能识别
这个特征,能推测是什么数字呢?只有越往后,检测识别的特征越多,试过能识别![]() 这几个特征,那么我就能够确定这个数字是“0”。
这几个特征,那么我就能够确定这个数字是“0”。
3.有stride_w和stride_h,后者表示的就是上下步长。如果用stride,则表示stride_h=stride_w=stride。