什么是反向传播
BP(back propagation)算法是利用复合函数的链式法则求解多层复合函数的所有变量的偏导数的有效方法。也可以说 ,反向传播,主要是链式法则的反复应用。(链式法则是微积分中的求导法则,用于求一个复合函数的导数)
一个简单的反向传播的例子
一个简单的网络结构图可以表示如下图所示:
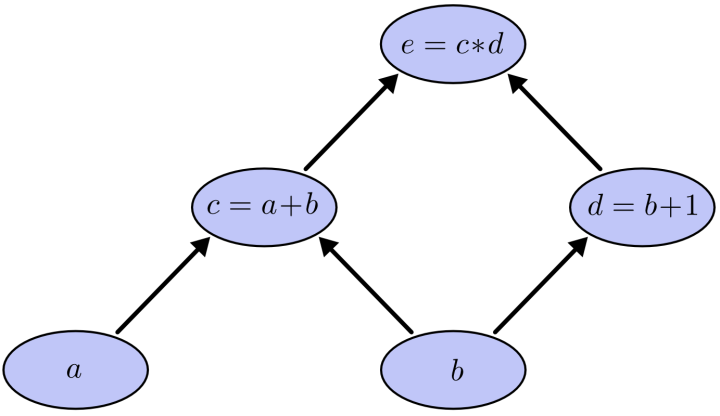
图片来源于网络
其中(a),(b)是输入,(c),(d)相当于隐藏层节点,(e)是输出,我们要求的是(e)对每一层节点的偏导数。
若输入(a=2,b=1),利用前向传播,我们可以从输入到输出一层一层地计算出每一个节点的值,即(c=a+b=3,d=b+1=2,e=c*d=6)。
而反向传播,则是从输出到输入一层一层地计算输出(e)到每个节点的偏导数的值,即计算输出(e)对于节点(c,d,a,b)的偏导数的值。首先利用偏导数的定义我们可以求出不同层相邻节点之间的偏导数的值如下图所示:
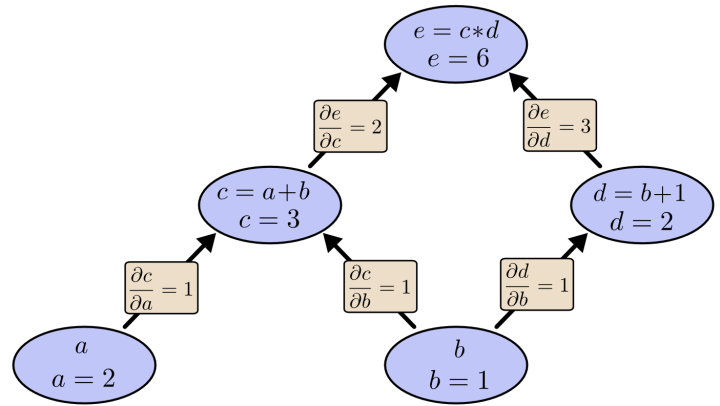
图片来源于网络
如上图所示,我们很容易地计算出了(frac{partial e}{partial c}=2,frac{partial e}{partial d}=3)。节点(e)到节点(a)有一条路径,即(e ightarrow c ightarrow a),那么(e)对于(a)的偏导数则为该条路径上所有相邻节点的偏导数的乘积,也就是(frac{partial e}{partial a}=frac{partial e}{partial c}cdot frac{partial c}{partial a}=2 imes 1=2)。(e)到(b)有两条路径,即(e ightarrow c ightarrow b)和(e ightarrow d ightarrow b),那么(e)对于(b)的偏导数则为这两条路径上所有相邻节点的偏导数的乘积的和,也就是(frac{partial e}{partial b}=frac{partial e}{partial c}cdot frac{partial c}{partial b}+frac{partial e}{partial d}cdot frac{partial c}{partial b}=2 imes 1+3 imes 1=5)。
一个基本的神经网络模型中反向传播的例子
一个基本的神经网络模型可以表示为如下图所示:
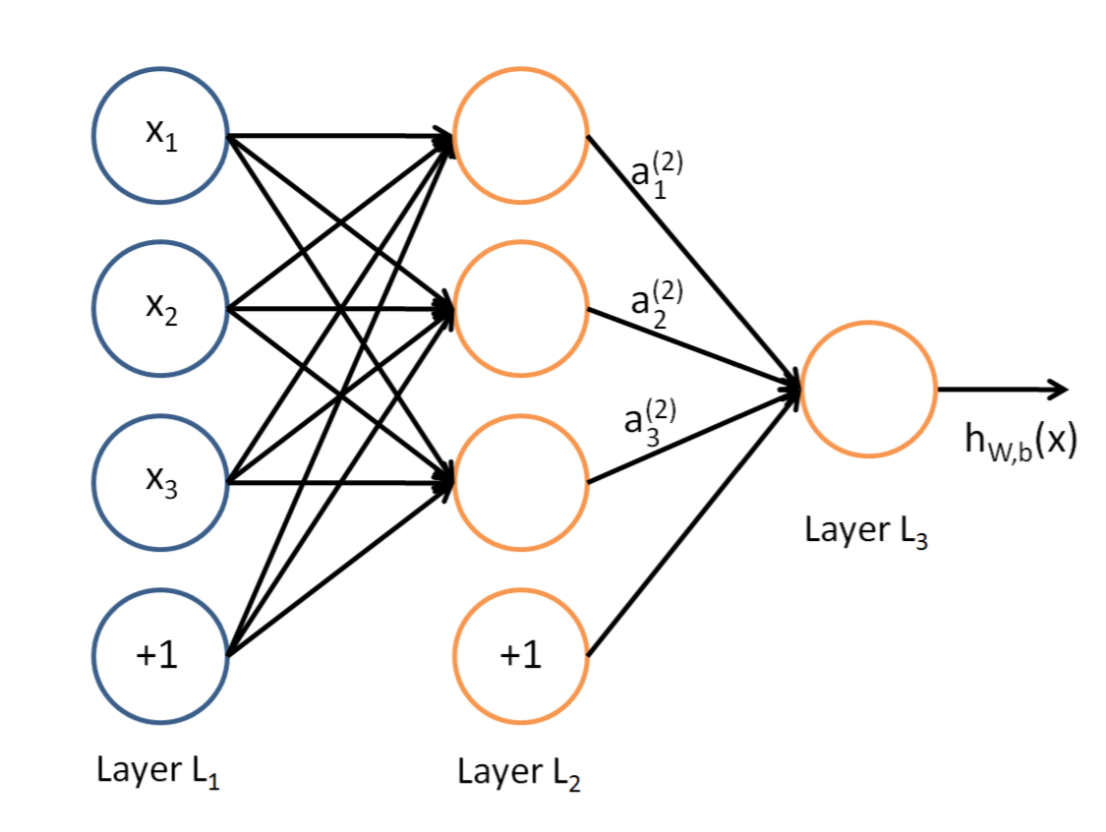
图片来源于网络
其中(L_1)层是输入层,(L_2)层是隐藏层,(L_3)层是输出层。
(未完待续)
参考文献: