一、TensorFlow中的优化器
- tf.train.GradientDescentOptimizer:梯度下降算法
- tf.train.AdadeltaOptimizer
- tf.train.AdagradOptimizer
- tf.train.MomentumOptimizer:动量梯度下降算法
- tf.train.AdamOptimizer:自适应矩估计优化算法
- tf.train.RMSPropOptimizer
- tf.train.AdagradDAOptimizer
- tf.train.FtrlOptimizer
- tf.train.ProximalGradientDescentOptimizer
- tf.train.ProximalAdagradOptimizertf.train.RMSProOptimizer
(1)如果数据是稀疏的,使用自适应学习方法。
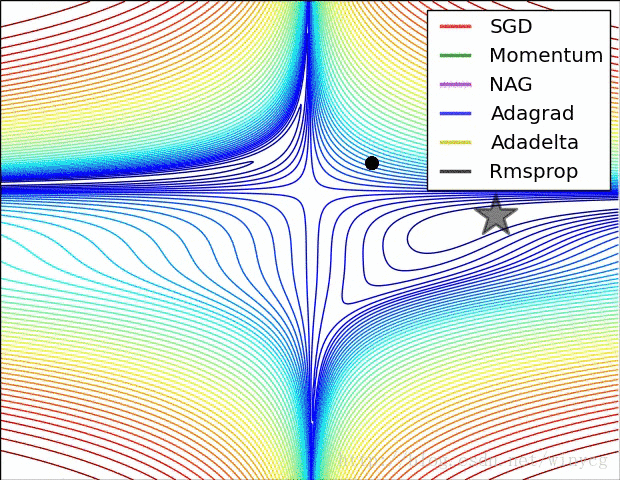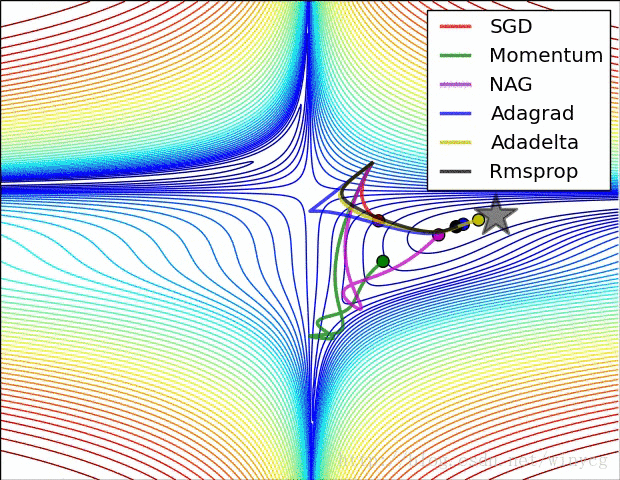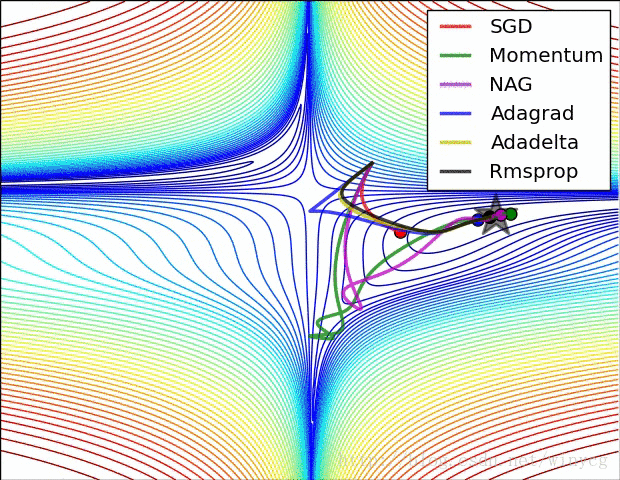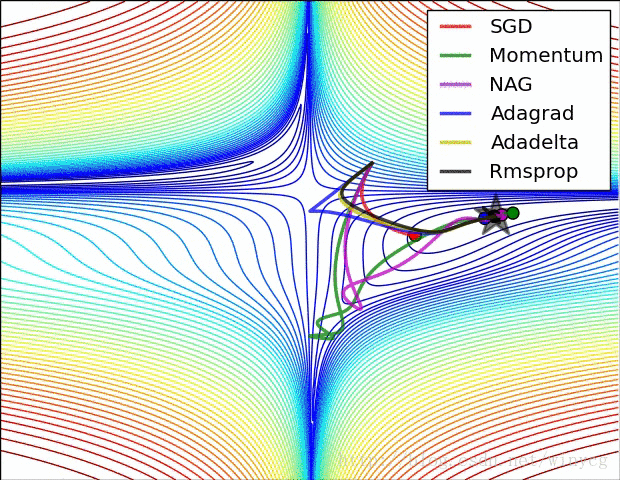
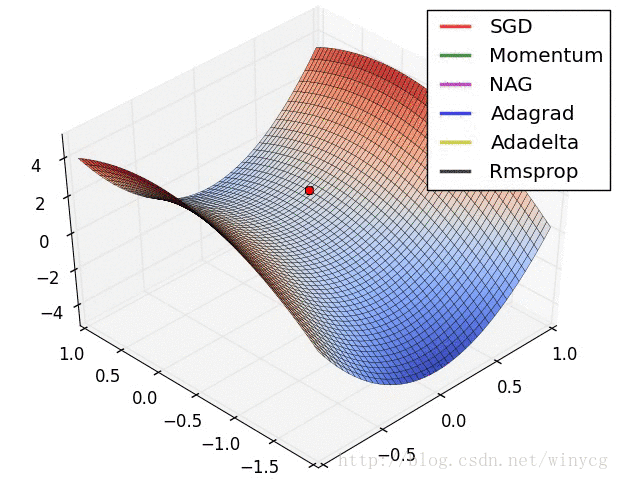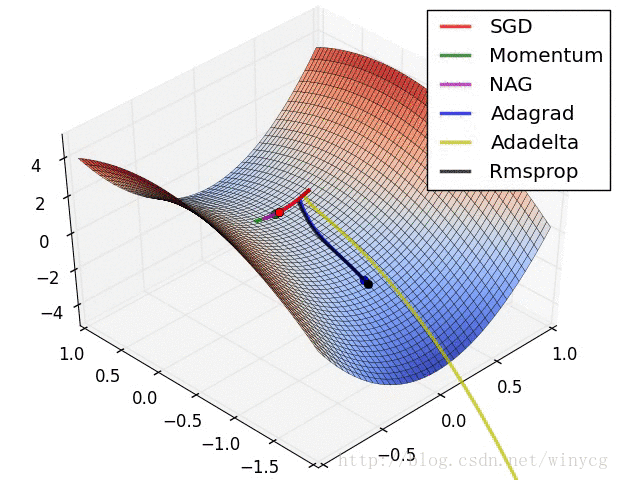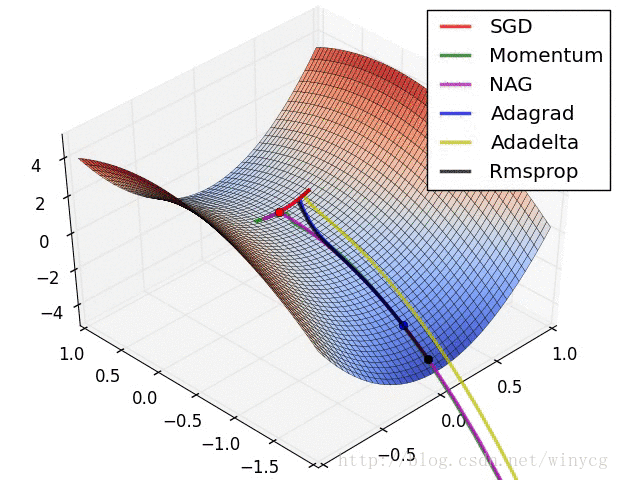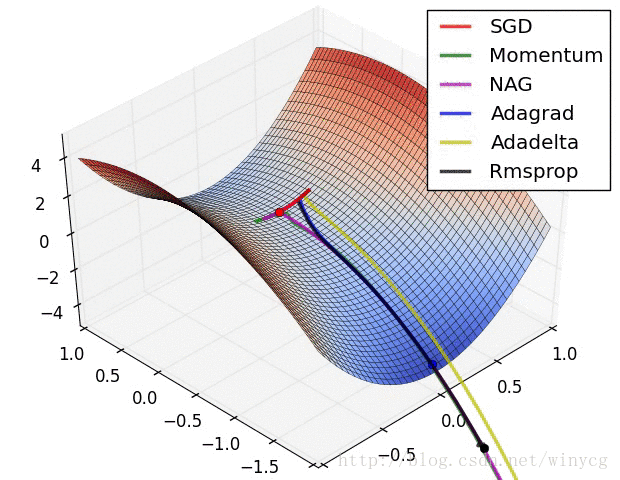
(2)RMSprop,Adadelta,Adam是非常相似的优化算法,Adam的bias-correction帮助其在最后优化期间梯度变稀疏的情况下略微战胜了RMSprop。整体来讲,Adam是最好的选择。
(3)很多论文中使用vanilla SGD without momentum。SGD通常能找到最小值,但是依赖健壮的初始化,并且容易陷入鞍点。因此,如果要获得更快的收敛速度和训练更深更复杂的神经网络,需要选择自适应学习方法。
https://blog.csdn.net/winycg/article/details/79363169
二、常用的种类:
1、tf.train.Optimizer:
2、tf.train.GradientDescentOptimizer:梯度下降
原理:
-
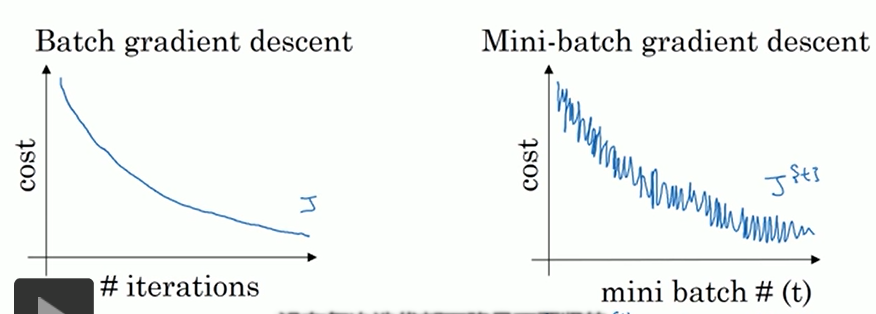
batch GD【全部样本,速度慢】
-
随机GD【随机一个样本,速度快,但局部最优】
-
mini-batch GD 【batch个样本,常在数据量较大时使用】
训练集样本数少【≤2000】:采用batchGD
训练集样本数多:采用mini-batch GD,batch大小一般为64-512. 训练时多尝试一下2的次方来找到最合适的batch大小。
应用:
这个类是实现梯度下降算法的优化器。这个构造函数需要的一个学习率就行了。
构造函数:tf.train.GradientDescentOptimizer(0.001).minimize(loss,global_step=None,var_list=None,gate_gradients=GATE_OP,aggregation_method=None,colocate_gradients_with_ops=False,name=None,grad_loss=None)

1 __init__( 2 3 learning_rate, 4 5 use_locking=False, 6 7 name='GradientDescent' 8 9 )
learning_rate: (学习率)张量或者浮点数
use_locking: 为True时锁定更新
name: 梯度下降名称,默认为"GradientDescent".
3、tf.train.AdadeltaOptimizer:
实现了 Adadelta算法的优化器,可以算是下面的Adagrad算法改进版本。
构造函数: tf.train.AdadeltaOptimizer.init(learning_rate=0.001, rho=0.95, epsilon=1e-08, use_locking=False, name=’Adadelta’)
4、tf.train.AdagradOptimizer:
构造函数:tf.train.AdagradOptimizer.__init__(learning_rate, initial_accumulator_value=0.1, use_locking=False, name=’Adagrad’)
5、tf.train.MomentumOptimizer:
原理:


momentum表示要在多大程度上保留原来的更新方向,这个值在0-1之间,在训练开始时,由于梯度可能会很大,所以初始值一般选为0.5;当梯度不那么大时,改为0.9。 α是学习率,即当前batch的梯度多大程度上影响最终更新方向,跟普通的SGD含义相同。
应用:
构造函数:tf.train.MomentumOptimizer.__init__(learning_rate, momentum, use_locking=False, name=’Momentum’, use_nesterov=False)

1 __init__( 2 3 learning_rate, 4 5 momentum, 6 7 use_locking=False, 8 9 name='Momentum', 10 11 use_nesterov=False 12 13 )
learning_rate: (学习率)张量或者浮点数
momentum: (动量)张量或者浮点数
use_locking: 为True时锁定更新
name: 梯度下降名称,默认为 "Momentum".
use_nesterov: 为True时,使用 Nesterov Momentum.
6、tf.train.RMSPropOptimizer
目的和动量梯度一样,减小垂直方向,增大水平方向。W为水平方向,b为垂直方向。

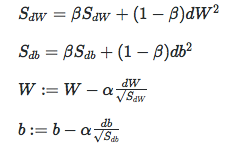
7、tf.train.AdamOptimizer:动量和RMSProp结合

应用:

1 __init__( 2 3 learning_rate=0.001, 4 5 beta1=0.9, 6 7 beta2=0.999, 8 9 epsilon=1e-08, 10 11 use_locking=False, 12 13 name='Adam' 14 15 )
构造函数:tf.train.AdamOptimizer.__init__(learning_rate=0.001, beta1=0.9, beta2=0.999, epsilon=1e-08, use_locking=False, name=’Adam’)
learning_rate: (学习率)张量或者浮点数,需要调试
beta1: 浮点数或者常量张量 ,表示 The exponential decay rate for the 1st moment estimates.【推荐使用0.9】
beta2: 浮点数或者常量张量 ,表示 The exponential decay rate for the 2nd moment estimates.【推荐使用0.999】
epsilon: A small constant for numerical stability. This epsilon is "epsilon hat" in the Kingma and Ba paper (in the formula just before Section 2.1), not the epsilon in Algorithm 1 of the paper.
use_locking: 为True时锁定更新
name: 梯度下降名称,默认为 "Adam".
8、Lookahead、LazyOptimizer、MaskedAdamOptimizer、AdaBound(转载)
(1)AdaBound算法:像Adam一样快,又像SGD一样好的优化器
SGD的缺点:
SGD现在后期调优时还是经常使用到,但SGD的问题是前期收敛速度慢。SGD前期收敛慢的原因: SGD在更新参数时对各个维度上梯度的放缩是一致的,并且在训练数据分布极不均很时训练效果很差。而因为收敛慢的问题应运而生的自适应优化算法Adam、AdaGrad、RMSprop 等,但这些自适应的优化算法虽然可以在训练早期展现出快速的收敛速度,但其在测试集上的表现却会很快陷入停滞,并最终被 SGD 超过。
Adam等自适应学习率算法缺点:
这就是目前很多大牛任然喜欢SGD的原因。这篇文章对于Adam后期的毛病进行了分析,原因出在自适应方法训练后期不稳定的极端学习率。换句话说,就是自适应学习率训练到后期,学习率出现极端情况,更新参数时有些维度上学习率特别大,有些维度学习率特别小。
采样参数的学习率,每个单元格包含一个通过对学习率进行数值运算得到的值,颜色越浅代表学习率越小。
我们可以看到,当模型接近收敛时,学习率中有大量的极端值(包含许多小于 0.01 和大于 1000 的情况)。这一现象表明在实际训练中,极端学习率是实际存在的。
发现这个问题怎么解决?如何融合上面两种方法的优点?
那就对自适应学习率加一下限制吧。具体做法是对学习率进行动态裁剪,在这一设置下,在训练早期由于上下界对学习率的影响很小,算法更加接近于 Adam;而随着时间增长裁减区间越来越收紧,模型的学习率逐渐趋于稳定,在末期更加贴近于 SGD。AMSBound 可以对 AMSGrad 采用类似的裁剪得到。
换句话说,Adam和SGD是AdaBound的特殊情况。
在这一设置下,在训练早期由于上下界对学习率的影响很小,算法更加接近于 Adam;而随着时间增长裁减区间越来越收紧,模型的学习率逐渐趋于稳定,在末期更加贴近于 SGD。AMSBound 可以对 AMSGrad 采用类似的裁剪得到。
(2)Lookahead
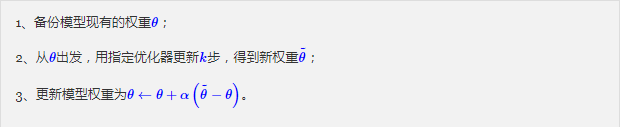
Lookahead的思路很朴素,准确来说它并不是一个优化器,而是一个使用现有优化器的方案。简单来说它就是下面三个步骤的循环执行:
(3)LazyAdam、MaskedAdamOptimize
LazyAdam
和图像等领域不同,对 NLU 之类的任务,每个 batch 采样到的词有限,每次更新对 Embedding 的梯度估计都是稀疏的。非 momentum-based 的 Optimizer 每步只会更新采样到的词,而对于所有带动量的优化器(自然也就包括Adam以及带动量的SGD)都存在一个问题:当前batch中没被采样到的词,依然会使用历史动量来更新,这可能导致Embedding层过拟合。具体来说,当一个词的被采样过后,它的Embedding的梯度不为0,这个梯度也会被记录在动量中,实际更新是用动量去更新的;在后面的batch中,假如该词没有被采样到,它的Embedding的梯度为0,但是它的动量并不为0,所以该词还是被更新了。这样一来就算没有被反复采样的词,对应的Embedding也被反复更新了,就导致了过拟合。
所以,一个改进的方案是只有当该词被采样过才更新,这就是LazyOptimizer的基本原理了。
LazyAdam是Adam的变体,可以更有效地处理稀疏更新。原始的Adam算法为每个可训练变量维护两个移动平均累加器,累加器在每一步都会更新**。 而此类为稀疏变量提供了更加懒惰的梯度更新处理,它仅更新当前batch中出现的稀疏变量索引的移动平均累加器,而不是更新所有索引的累加器。 与原始的Adam优化器相比,它可以为某些应用提供模型训练吞吐量的大幅改进。 但是它的语义与原始的Adam算法略有不同,可能会导致不同的实验结果。
在实现上,我们要如何判断一个词有没有被采样过呢?当然终极方法肯定是传入被采样过的词的index了,但这使用上不够友好。我这里使用了一个近似的方法:判断该词的Embedding对应的梯度是否为0,如果为0意味着它“很可能”在当前batch没有被采样到。背后的原理在于,如果它没有被采样到,那么梯度一定为0,如果它被采样到了,那么梯度为0的概率是非常小的,毕竟那么多分量,同时为0的可能性很小,所以这样实现也够用了。
AdamOptimizer源码中函数_apply_sparse和_resource_apply_sparse 主要用在稀疏向量的更新操作上,而具体的实现是在函数_apply_sparse_shared中
LazyAdam源码:
可以看出公式与Adam都相同,不同的是每次迭代根据当前batch的indices来对一阶动量和二阶动量进行更新。

def _apply_sparse(self, grad, Var): beta1_power, beta2_power = self._get_beta_accumulators() beta1_power = math_ops.cast(beta1_power, Var.dtype.base_dtype) beta2_power = math_ops.cast(beta2_power, Var.dtype.base_dtype) lr_t = math_ops.cast(self._lr_t, Var.dtype.base_dtype) beta1_t = math_ops.cast(self._beta1_t, Var.dtype.base_dtype) beta2_t = math_ops.cast(self._beta2_t, Var.dtype.base_dtype) epsilon_t = math_ops.cast(self._epsilon_t, Var.dtype.base_dtype) lr = (lr_t * math_ops.sqrt(1 - beta2_power) / (1 - beta1_power)) # \(m := beta1 * m + (1 - beta1) * g_t\) m = self.get_slot(Var, "m") m_t = state_ops.scatter_update(m, grad.indices, beta1_t * array_ops.gather(m, grad.indices) + (1 - beta1_t) * grad.Values, use_locking=self._use_locking)#一阶动量 # \(V := beta2 * V + (1 - beta2) * (g_t * g_t)\) V = self.get_slot(Var, "V") V_t = state_ops.scatter_update(V, grad.indices, beta2_t * array_ops.gather(V, grad.indices) + (1 - beta2_t) * math_ops.square(grad.Values), use_locking=self._use_locking) #二阶动量 # \(Variable -= learning_rate * m_t / (epsilon_t + sqrt(V_t))\) m_t_slice = array_ops.gather(m_t, grad.indices) V_t_slice = array_ops.gather(V_t, grad.indices) denominator_slice = math_ops.sqrt(V_t_slice) + epsilon_t Var_update = state_ops.scatter_sub(Var, grad.indices, lr * m_t_slice / denominator_slice, use_locking=self._use_locking) return control_flow_ops.group(Var_update, m_t, V_t)
Madam:

from tensorflow.python.ops import array_ops from tensorflow.python.training import adam from tensorflow.python.framework import ops from tensorflow.python.ops import control_flow_ops from tensorflow.python.ops import math_ops from tensorflow.python.ops import resource_variable_ops from tensorflow.python.ops import state_ops from tensorflow.python.ops import variable_scope from tensorflow.python.training import optimizer class MaskedAdamOptimizer(adam.AdamOptimizer): def _apply_sparse_shared(self, grad, var, indices, scatter_add): beta1_power, beta2_power = self._get_beta_accumulators() beta1_power = math_ops.cast(beta1_power, var.dtype.base_dtype) beta2_power = math_ops.cast(beta2_power, var.dtype.base_dtype) lr_t = math_ops.cast(self._lr_t, var.dtype.base_dtype) beta1_t = math_ops.cast(self._beta1_t, var.dtype.base_dtype) beta2_t = math_ops.cast(self._beta2_t, var.dtype.base_dtype) epsilon_t = math_ops.cast(self._epsilon_t, var.dtype.base_dtype) lr = (lr_t * math_ops.sqrt(1 - beta2_power) / (1 - beta1_power)) # m_t = beta1 * m + (1 - beta1) * g_t m = self.get_slot(var, "m") m_scaled_g_values = grad * (1 - beta1_t) m_t = state_ops.assign(m, m * beta1_t, use_locking=self._use_locking) with ops.control_dependencies([m_t]): m_t = scatter_add(m, indices, m_scaled_g_values) # v_t = beta2 * v + (1 - beta2) * (g_t * g_t) v = self.get_slot(var, "v") v_scaled_g_values = (grad * grad) * (1 - beta2_t) v_t = state_ops.assign(v, v * beta2_t, use_locking=self._use_locking) with ops.control_dependencies([v_t]): v_t = scatter_add(v, indices, v_scaled_g_values) gather_m_t = array_ops.gather(m_t, indices) gather_v_t = array_ops.gather(v_t, indices) gather_v_sqrt = math_ops.sqrt(gather_v_t) var_update = scatter_add(var, indices, -lr * gather_m_t / (gather_v_sqrt + epsilon_t)) return control_flow_ops.group(*[var_update, m_t, v_t])
两者在计算移动平均累加器时(一阶动量和二阶动量)有所不同:
LazyAdam:

m_t = state_ops.scatter_update(m, grad.indices, beta1_t * array_ops.gather(m, grad.indices) + (1 - beta1_t) * grad.Values, use_locking=self._use_locking)
Madam:

m_scaled_g_Values = grad * (1 - beta1_t) m_t = state_ops.assign(m, m * beta1_t, use_locking=self._use_locking) with ops.control_dependencies([m_t]): m_t = scatter_add(m, indices, m_scaled_g_Values)
Madam其实是介于Lazy Adam和 Adam之间的一种方法,其与Lazy Adam唯一的不同在于对一阶动量m和二阶动量 V 进行 decay 的操作,Madam是全部都要 decay,即当前batch没有采样到的变量所对应的之前动量的累积值也要考虑。 而LazyAdam 是只 decay 采样到的embedding。(在计算指数加权平均时,LazyAdam只对当前采样到的变量之前的平均值进行累加,没有采样到的样本不累加,而Madam要全部累加)。
LazyAdam存在的一个问题是当梯度为0时不更新对应的m和v。实际上当其他权重改变时m和v应该更新。Madam应该是解决了这个问题所以性能变得更好。
为了更形象的说明它们的差异,通过一个假设的例子来说明,用一阶动量来举例:
MaskedAdamOptimize
来源:知乎
AllenNLP 也在 2018 EMNLP 的 Tutorial 里面提到。
和图像等领域不同,对 NLU 之类的任务,每个 batch 采样到的词有限,每次更新对 Embedding 的梯度估计都是稀疏的。非 momentum-based 的 Optimizer 每步只会更新采样到的词,而对于 momentum-based 的 Optimizer,现在所有框架的实现都会用当前的 momentum 去更新所有的词,即使这些词在连续的几十步更新里都没有被采样到。这可能会使 Embedding 过拟合。
下面是一个文本分类问题在不同 setting 下对应的 valid set 准确率曲线。learning rate 固定不变。madam 指的是修正过后的 adam,LoEmbed 表示是否加载预训练的词向量。在加载词向量的 setting 下,不加修正的 Adam 过拟合的不能看。

代码:

# for tensorflow 1.12.0 from tensorflow.python.ops import array_ops from tensorflow.python.training import adam from tensorflow.python.framework import ops from tensorflow.python.ops import control_flow_ops from tensorflow.python.ops import math_ops from tensorflow.python.ops import resource_variable_ops from tensorflow.python.ops import state_ops from tensorflow.python.ops import variable_scope from tensorflow.python.training import optimizer class MaskedAdamOptimizer(adam.AdamOptimizer): def _apply_sparse_shared(self, grad, var, indices, scatter_add): beta1_power, beta2_power = self._get_beta_accumulators() beta1_power = math_ops.cast(beta1_power, var.dtype.base_dtype) beta2_power = math_ops.cast(beta2_power, var.dtype.base_dtype) lr_t = math_ops.cast(self._lr_t, var.dtype.base_dtype) beta1_t = math_ops.cast(self._beta1_t, var.dtype.base_dtype) beta2_t = math_ops.cast(self._beta2_t, var.dtype.base_dtype) epsilon_t = math_ops.cast(self._epsilon_t, var.dtype.base_dtype) lr = (lr_t * math_ops.sqrt(1 - beta2_power) / (1 - beta1_power)) # m_t = beta1 * m + (1 - beta1) * g_t m = self.get_slot(var, "m") m_scaled_g_values = grad * (1 - beta1_t) m_t = state_ops.assign(m, m * beta1_t, use_locking=self._use_locking) with ops.control_dependencies([m_t]): m_t = scatter_add(m, indices, m_scaled_g_values) # v_t = beta2 * v + (1 - beta2) * (g_t * g_t) v = self.get_slot(var, "v") v_scaled_g_values = (grad * grad) * (1 - beta2_t) v_t = state_ops.assign(v, v * beta2_t, use_locking=self._use_locking) with ops.control_dependencies([v_t]): v_t = scatter_add(v, indices, v_scaled_g_values) gather_m_t = array_ops.gather(m_t, indices) gather_v_t = array_ops.gather(v_t, indices) gather_v_sqrt = math_ops.sqrt(gather_v_t) var_update = scatter_add(var, indices, -lr * gather_m_t / (gather_v_sqrt + epsilon_t)) return control_flow_ops.group(*[var_update, m_t, v_t])
Tensorflow 有个叫 LazyAdamOptimizer 的方案,但试下来稳定比这个实现差。
