一、关联规则
1、是数据中所蕴含的一类重要规律，对关联规则挖掘的目标是在数据项目中找出所有的并发关系，这种搞关系也称为关联。
eg、奶酪->啤酒[支持度 = 10%，置信度 = 80%]
2、关联规则的基本概念
设一个项目集合I = {i1,i2,i3,……,im}，一个（数据库）事务集合T = {t1,t2,t3,,,tn}，其中每个事务ti是一个项目集合，并且
。
一个关联规则是如下形式的蕴涵关系：
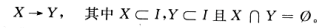
3、关联规则强度指标：支持度和置信度
（1）支持度：规则X->Y的支持度是指，T中包含
的事务的百分比。支持度是一个很有用的评价指标，如果他的值过于的小，则表明时间可能只是偶然发生
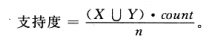
（2）置信度：决定了规则的可预测度，表示在所有发生了X的事务中同样发生了Y的概率。
二、Apriori算法
1、Apriori原理：Apriori算法基于演绎Apriori原理（向下封闭属性）
向下封闭属性（Downward Closure Property）：如果一个项目集满足某个最小支持的度要求，那么这个项集的任何非空子集必需都满足这个最小支持度。
为了确保频繁项目集成的高效性，Apriori算法假定I中的项目都是排序好的。
2、描述
就是对于数据集D，遍历它的每一条记录T，得到T的所有子集，然后计算每一个子集的支持度，最后的结果再与最小支持度比较。且不论这个数据集D中有多少条记录（十万？百万？），就说每一条记录T的子集个数（{1,2,3}的子集有{1}，{2}，{3}，{1,2}，{2,3}，{1,3}，{1,2,3}，即如果记录T中含有n项，那么它的子集个数是2^n-1）。计算量非常巨大，自然是不可取的。
所以Aprior算法提出了一个逐层搜索的方法，如何逐层搜索呢？包含两个步骤：
1.自连接获取候选集。第一轮的候选集就是数据集D中的项，而其他轮次的候选集则是由前一轮次频繁集自连接得到（频繁集由候选集剪枝得到）。
2.对于候选集进行剪枝。如何剪枝呢？候选集的每一条记录T，如果它的支持度小于最小支持度，那么就会被剪掉；此外，如果一条记录T，它的子集有不是频繁集的，也会被剪掉。
算法的终止条件是，如果自连接得到的已经不再是频繁集，那么取最后一次得到的频繁集作为结果。