在理解红黑树之前,先了解下二叉树的特性。
(1)左子树上节点的值小于等于其根节点的值。(2)右子树上节点的值大于等于其根节点的值。(3)左、右子树也分别为二叉排序树。
如下图所示,比如我们要查询8 ,第一次9>8,所以找到了9的左子树5;第二次8>5,找到了5的右子树7;第三次7<8,找到了7的右子树8。其实就是利用了二分法的特性进行了查询,时间复杂度也在lgN。
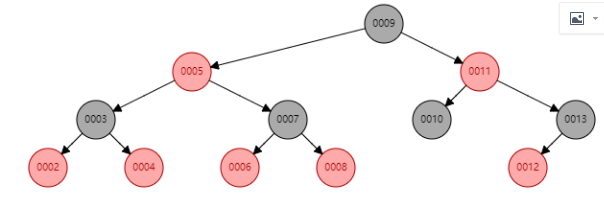
但是也会有那种不平衡的二叉树,就是左子树深度和右子树深度存在明显的差异,那这样我们要查询一棵树的话,可能要一直遍历下去,如下图所示,则要一直遍历其右子树。这样查询的时间复杂度将趋近于n。和数组查询某个元素的值的时间复杂度相同了。所以基于这种情况,引入了平衡二叉树,而红黑树正好是平衡二叉树的一种。
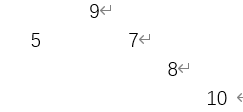
红黑树的几个特性
1.节点是黑色或者红色。
2.根节点是黑色的。
3.所有得叶节点都是黑色,(这里说得都说NULL节点)。
4.每个红色的子节点一定都是黑色,也就是不存在两个连续的红色节点。
5.从任意节点到其每个子节点的所有路径都包含相同数目的黑色节点。
推荐一个超nice的链接,在线构造红黑树:https://rbtree.phpisfuture.com/ 会发现当不满足红黑树特性得时候,会通过旋转来达到符合红黑树得规则。 红黑树得旋转参考链接:https://blog.csdn.net/u011240877/article/details/53329023#%E6%8C%87%E5%AE%9A%E8%8A%82%E7%82%B9-x-%E7%9A%84%E5%B7%A6%E6%97%8B-%E5%8F%B3%E5%9B%BE%E8%BD%AC%E6%88%90%E5%B7%A6%E5%9B%BE
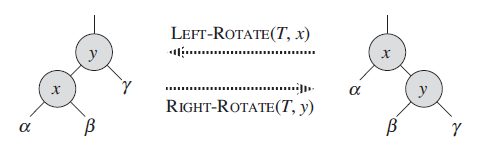
x节点左旋(右图转到左图)
p: x
r: y
if(p!= null){
Entry<K,V> r = p.right;
p.right = r.left;
if(r.left != null){
r.left.parent = p; //设置β的父亲为x
}
r.parent = p.parent; //设置y的父亲是x的父亲
if(p.parent == null){ //如果x没有父亲,则y就是最老得根节点
root = r
}else if(p.parent.left == p){ //如果x有父亲并且它是它父亲得左孩子,则x得父亲认y为左孩子
p.parent.left = r;
}else{
p.parent.rgiht = r; //如果x是它父亲得右孩子,父亲就认y为右孩子
}
r.left = p; //y逆袭成功,x成为了它得左孩子
p.parent = r;
}
节点y得右旋(左图转到右图)
p:x
r:y
if(r != null){
Entry<K,V> p = r.left;
r.left = p.right
if(p.right != null){
p.right.parent = r; //设置β的父亲为y
}
p.parent = r.parent;
if(r.parent == null){ //判断y是否存在父节点,若不存在,则x升级为根节点
root = p;
}else if(r.parent.left == r){ //若y存在父节点,并且是其父节点得左子树得话,那么x升级为y得父节点得右左节点
r.parent.left = p;
}else{
r.parent.right = p; //若y存在父节点,并且是其父节点得右子树得话,那么x升级为y得父节点得右节点
}
p.right = r; //x升级成功,y成了x得右节点
r.parent = p; //y得父节点更新为x
}
总结: (1)当插入一个节点时,默认是红色得。如果当父节点也是红色,则向上递归换色。如果跟节点变为红色,则对其旋转,旋转方向根据左右节点深度,若左节点过深,则向右旋转;之后再从根节点,依次向下修改颜色 。
(2)从根节点到红色节点,符合得路径上面校验黑色节点数量是否一致,,如果不一致,那同样和(1)中一样,先旋转,再修改颜色。 前面推荐得链接,尽量多试试,有助于理解。