18.9.8 考试总结

这道题就是树上贪心就好了 从下往上搞 要是遇到没有被选过得点就把他的父亲标记就好了

然后就 $bfs$ 把节点都存到一个栈里面 然后弹出的肯定是最深的点 就慢慢往上搞就可以了

代码

#include <bits/stdc++.h>
using namespace std;

const int N = 1e5 + 5;
int stk[N],tot,top,fa[N],ans = 0;
int n,head[N],nex[2 * N],tov[2 * N];
bool vis[N],arr[N];
queue<int>Q;

void add(int u,int v) {
    
    tot ++;
    nex[tot] = head[u];
    tov[tot] = v;
    head[u] = tot;
}

void add_Edge( ) {
    
    scanf("%d",& n);
    for(int i = 1;i < n;i ++) {
        int u,v;
        scanf("%d%d",& u,& v);
        add(u,v); add(v,u);
    }
}

void BFS( ) {
    
    Q.push(1); stk[++ top] = 1;
    vis[1] = true;
    while(! Q.empty( )) {
        int u = Q.front( ); Q.pop( );
        for(int i = head[u];i;i = nex[i]) {
            int v = tov[i];
            if(vis[v]) continue;
            vis[v] = true; fa[v] = u;
            Q.push(v); stk[++ top] = v;
        }
    }
}

void Solve( ) {
    
    while(top) {
        if(arr[stk[top]]) {
            top --; continue;
        }
        else {
            int u = stk[top];
            ans ++;
            arr[fa[u]] = true;
            for(int i = head[fa[u]];i;i = nex[i]) {
                int v = tov[i];
                arr[v] = true;
            }
        }
        top --;
    }
    printf("%d",ans);
}

int main( ) {
    
    freopen("CP.in","r",stdin);
    freopen("CP.out","w",stdout);
    add_Edge( );
    BFS( );
    Solve( );
}

啊这道题很神奇 有点类似倍增 因为所有的方案总是要求一个能够覆盖所有的区间并

所以必定有一个区间是经过原点的 所以就枚举这个区间是什么 然后判断就可以了

至于判断就是 因为他是一个环 所以就常规套路 把环复制一边当作链处理

这个时候答案就是现在序列的能够从$n$ 走到$2n$的最少步数

对于数据我们可以发现有些区间是没有用处的 即那些左右端点都被别的一个区间包裹住的区间就没用

所以在跑之前就先把这些没用的区间筛去就可以了 有点类似于单调栈的思想

所以这个时候我们得到了一个左右端点均单调递增的区间序列 这时候就可以通过二分找出这个区间的$nex$是谁

$nex$就是他的连在一起的右端点能够延伸最远的区间 这样子按照贪心肯定是最优秀的

然后就是两个 $dp$ 数组了 $f[i]$表示第 $i$ 号区间跳到$2n$这个位置的步数

$g[i]$表示他最终跳到超过$2n$位置时在那个区间 有什么用呢

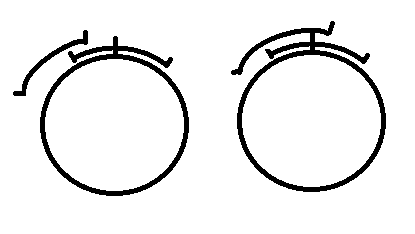
如果是右边的情况 就没有问题 但是如果是左边的情况 那么这个时候不用越过$2n$就可以走完了 所以答案要减一

所以判断就是他走到终点的那个区间等于他自己 $g[i]$就是拿来干这个的

至于转移还是很简单 

　　　　$f[i] = f[nex[i]] + 1$          $g[i] = g[nex[i]]$ 

边界就是最后那个右端点大于$2n$的  $f[i] = 1$  $g[i] = i$

然后最后就是答案就是$min(f[i])$(要满足条件)

代码

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int N = 1e5 + 5;
struct data {
    
    ll l,r;
    data(ll l = 0,ll r = 0): l(l),r(r) { }
}a[N],q[2 * N];

int n,m,f[2 * N],g[2 * N],cnt = 0,nex[N],ans;

bool cmp(const data & a,const data & b) {
    
    return a.l < b.l;
}

void init( ) {
    
    sort(a + 1,a + m + 1,cmp);
    for(int i = m;i >= 1;i --) {
        while(q[cnt].r <= a[i].r && cnt) 
            cnt --;
        q[++ cnt] = a[i];
    }
    reverse(q + 1,q + cnt + 1);
    for(int i = 1;i <= cnt;i ++) 
        q[i + cnt] = q[i],q[i + cnt].l += n,q[i + cnt].r += n;
}

int find_pos(int pos) {
    
    int l = pos,r = 2 * cnt,ans = 1 + 2 * cnt;
    while(l <= r) {
        int mid = (l + r) >> 1;
        if(q[mid].l <= q[pos].r) ans = mid,l = mid + 1;
        else r = mid - 1;
    }
    return ans;
}

void Solve( ) {
    
    for(int i = 1;i <= cnt * 2;i ++) {
        nex[i] = find_pos(i);
    }
    for(int i = 2 * cnt;i >= 1;i --) 
        if(q[i].r >= 2 * n) f[i] = 1,g[i] = i;
        else f[i] = f[nex[i]] + 1,g[i] = g[nex[i]];
    ans = 10000000;
    for(int i = 1;i <= cnt;i ++) {
        if(q[i].r >= n) {
            ans = min(ans,f[i] - ((g[i] - cnt) == i));
        }
    }
    printf("%d",ans);
}

int main( ) {
    
    freopen("gfw.in", "r", stdin);
    freopen("gfw.out", "w", stdout);
    scanf("%d%d",& n,& m);
    for(int i = 1;i <= m;i ++) {
        ll L,R;
        scanf("%lld%lld",& L,& R);
        a[i] = data(L,R + L);
    }
    init( );
    Solve( );
}

一看到这道题 我以为是他那个是noip类似的那个题 叫运输计划 就是二分答案 然后把不合法的情况 求一个重边就可以了

这个东西乍一看非常难 实际上只是一道简单的高中线性规划

这样子考虑 对于一个建立的 $x -> y$ 的传送站 一个$l -> r$ 的任务

那么他所需要花费的时间就是$|l - x| + |r - y|$  画个图就清楚了

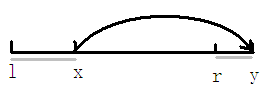
至于终点小于$r$是很直观的 自己画画图就出来了 然后这玩意儿要小于等于枚举的最大时间p

所以打开括号就可以得到关于$x + y$ 和$x - y$的两个不等式

这个时候就求边界然后判断有没有可行解就可以了 然后边界要赋值$1e9$ 我在这上面改了半天

代码

#include <bits/stdc++.h>
#define oo 1000000000
using namespace std;

typedef long long ll;
const int N = 5 * 1e5 + 5;
struct Cmd {
    ll l,r;
}a[N];
ll n,m;

bool check(ll p) {
    
    ll L1 = -oo,R1 = oo,L2 = -oo,R2 = oo;
    for(int i = 1;i <= m;i ++) {
        if(a[i].r - a[i].l > p) {
            L1 = max(L1,a[i].r + a[i].l - p);
            L2 = max(L2,a[i].r - a[i].l - p);
            R1 = min(R1,a[i].l + a[i].r + p);
            R2 = min(R2,a[i].r - a[i].l + p);
        }
    }
    return L1 <= R1 && L2 <= R2;
}

int main( ) {
    
    freopen("bricks.in","r",stdin);
    freopen("bricks.out","w",stdout);
    scanf("%lld%d",& n,& m);
    for(int i = 1;i <= m;i ++) {
        scanf("%lld%lld",& a[i].l,& a[i].r);
        if(a[i].l > a[i].r) swap(a[i].l,a[i].r);
    }
    ll l = 0,r = oo,ans = oo;
    while(l <= r) {
        int mid = (l + r) >> 1;
        if(check(mid)) ans = mid,r = mid - 1;
        else l = mid + 1;
    }
    printf("%lld",ans);
}