
这道题是一道矩阵乘法的题 我只想说 我恨矩阵乘法一辈子
然后这道题是$n * m$可以过得 所以对应乘出来之后的新矩阵 它对应的区域的贡献可以转移到原矩阵上面
画个图
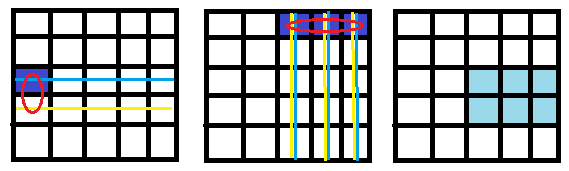
新矩阵中的蓝色区域 是由蓝色的线分别点乘起来得到的 黄色的线分别点乘 所以对于右边紫色方块的贡献
就是分别和左边的紫色乘起来 那么那一列的贡献就是红色圈圈区域的和的乘积 再在两矩阵的对应列对应行分别乘起来就好了
代码
#include <bits/stdc++.h> using namespace std; const int N = 2000 + 5; int s1[N][N],s2[N][N],a[N][N],b[N][N],n,m,cnt; long long ans; void Init( ) { scanf("%d%d",& n,& m); for(int i = 1;i <= n;i ++) for(int j = 1;j <= n;j ++) scanf("%d",& a[i][j]); for(int i = 1;i <= n;i ++) for(int j = 1;j <= n;j ++) { scanf("%d",& b[i][j]); s2[i][j] = s2[i][j - 1]+ b[i][j]; } for(int i = 1;i <= n;i ++) { for(int j = 1;j <= n;j ++) { s1[i][j] = s1[i][j - 1] + a[j][i]; } } } void Solve( ) { while(m --) { int a,b,c,d; scanf("%d%d%d%d",& a,& b,& c,& d); if(a > c) swap(a, c); if(b > d) swap(b, d); ans = 0; for(int i = 1;i <= n;i ++) { int aa = s1[i][c] - s1[i][a - 1]; int bb = s2[i][d] - s2[i][b - 1]; ans += 1ll * aa * bb; } printf("%lld ",ans); } } int main( ) { freopen("matrix.in","r",stdin); freopen("matrix.out","w",stdout); Init( ); Solve( ); }

这道题只要知道一个结论就变得炒鸡简单了 先要知道这玩意儿求的是两点间的曼哈顿距离
对于一些点 要求一个点 是他们到这个点的曼哈顿距离最小 这个点$(x,y)$
$x$是所有$x$的中位数 $y$也一样
所以就枚举这个点的坐标 然后$O(n)$求出每个点到这个点的曼哈顿距离 排排序取前几个就可以了
代码
#include <bits/stdc++.h> #define oo 2 * 1e9 using namespace std; const int N = 100; int n,x[N],y[N],dis[N]; void Init( ) { scanf("%d",& n); for(int i = 1;i <= n;i ++) scanf("%d%d",& x[i],& y[i]); } int solve(int xx,int yy,int tim) { int ans = 0; for(int i = 1;i <= n;i ++) { dis[i] = abs(x[i] - xx) + abs(y[i] - yy); } sort(dis + 1,dis + n + 1); for(int i = 1;i <= tim;i ++) { ans += dis[i]; } return ans; } void Solve( ) { for(int t = 1;t <= n;t ++) { if(t == 1) {printf("0 "); continue;} int ans = oo; for(int i = 1;i <= n;i ++) { for(int j = 1;j <= n;j ++) { ans = min(ans,solve(x[i], y[j], t)); } } printf("%d ",ans); } } int main( ) { freopen("tower.in","r",stdin); freopen("tower.out","w",stdout); Init( ); Solve( ); }

这道题是一道$dp$ $dp[u][0 / 1]$ 表示以$u$为根的子树 $u$是否和其儿子匹配的最大匹配数
$g[u][0 / 1]$表示方案数
转移
$dp[u][0] = ∑max(dp[v][0 / 1])$
$dp[u][1]$ 枚举儿子 保证其中一个必须选$dp[v][0]$来和$u$匹配 剩余一样选择
方案数一样的 从哪里转移过来就用那里的$g$ 然后用乘法原理将各个儿子乘一乘就好了
如果$dp$一样的 就将$g$加起来就可以了
然后这玩意儿要高精度 我就懒得写了...贴一个没有高精度的60分垃圾代码qwqwqwqwqwqwqwq
代码
#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 1e3 + 5; int n; ll dp[N][2],g[N][2]; vector<int>s[N]; void Init( ) { scanf("%d",& n); for(int i = 1;i <= n;i ++) { int u,v,m; scanf("%d%d",& u,& m); for(int j = 1;j <= m;j ++) { scanf("%d",& v); s[u].push_back(v); } } } void Dfs(int u,int fa) { g[u][0] = 1; int siz = s[u].size( ); for(int i = 0;i < siz;i ++) { int v = s[u][i]; //if(v == fa) continue; Dfs(v, u); } for(int i = 0;i < siz;i ++) { int v = s[u][i]; if(v == fa) continue; if(dp[v][1] > dp[v][0]) dp[u][0] += dp[v][1],g[u][0] *= g[v][1]; else if(dp[v][1] < dp[v][0]) dp[u][0] += dp[v][0],g[u][0] *= g[v][0]; else dp[u][0] += dp[v][0],g[u][0] *= g[v][1] + g[v][0]; } for(int i = 0;i < siz;i ++) { int vv = s[u][i]; //if(vv == fa) continue; ll cmp = dp[vv][0],f = g[vv][0]; for(int j = 0;j < siz;j ++) { int v = s[u][j]; if(v == fa || j == i) continue; if(dp[v][1] > dp[v][0]) cmp += dp[v][1],f *= g[v][1]; else if(dp[v][1] < dp[v][0]) cmp += dp[v][0],f *= g[v][0]; else cmp += dp[v][0],f *= g[v][1] + g[v][0]; } if(cmp + 1 > dp[u][1]) {dp[u][1] = cmp + 1; g[u][1] = f; } else if(cmp + 1 == dp[u][1]) {g[u][1] += f; } } } void Solve( ) { ll ans; Dfs(1, 1); if(dp[1][0] > dp[1][1]) printf("%lld %lld",dp[1][0],g[1][0]); else if(dp[1][0] < dp[1][1]) printf("%lld %lld",dp[1][1],g[1][1]); else printf("%lld %lld",dp[1][0],g[1][0] + g[1][1]); } int main( ) { freopen("tree.in","r",stdin); freopen("tree.out","w",stdout); Init( ); Solve( ); }