Mode-Free Policy Evaluation: Policy Evaluation Without Knowing How the World Works
Policy evaluation without known dynamics & reward models
This Lecture: Policy Evaluation (这篇博文大纲)
- 在没有权限访问真实MDP模型的条件下估计一个特定策略的回报期望
- 动态规划
- 蒙特·卡罗尔策略评估
- 在没有一个建模world如何运转的模型下做策略评估
- 在给定on-policy的采样下
- 在没有一个建模world如何运转的模型下做策略评估
- 时序差分(Temporal Difference, TD)
- 评估和比较算法的标准
Recall

Dynamic Programming for Policy Evaluation
- Initializa V 0 π = 0 V_0^pi=0 V0π=0 for s
- For k = 1 until convergence
- For all s in S
- V k π = r ( s , π ( s ) ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s , π ( s ) ) V k − 1 π ( s ′ ) V_k^pi=r(s,pi(s))+gammasum_{s' in S}p(s'|s,pi(s))V_{k-1}^pi(s') Vkπ=r(s,π(s))+γ∑s′∈Sp(s′∣s,π(s))Vk−1π(s′)
- For all s in S
V
k
π
(
s
)
V_k^{pi}(s)
Vkπ(s) is exact value of k-horizon value of state s under policy
π
pi
π。
V
k
π
(
s
)
V_k^pi(s)
Vkπ(s) is an estimate of infinite horizon value of state s under policy。
V
π
(
s
)
=
E
π
[
G
t
∣
s
t
=
s
]
≈
E
[
r
t
+
γ
V
k
−
1
∣
s
t
=
s
]
V^{pi}(s) = mathbb{E}_pi[G_t|s_t=s]approxmathbb{E}[r_t+gamma V_{k-1}|s_t=s]
Vπ(s)=Eπ[Gt∣st=s]≈E[rt+γVk−1∣st=s]
k越大,这越是一个好的近似;k越小,这越是一个差的近似。
收敛判定条件:
∥
V
k
π
−
V
k
−
1
π
∥
<
ϵ
|V_k^pi-V_{k-1}^pi|<epsilon
∥Vkπ−Vk−1π∥<ϵ
当然,该算法是在已给定动态/变迁模型P的条件下运行。
图形化描述,注意图中文字。

Policy Evaluation: V π ( s ) = E [ G t ∣ s t = s ] V^pi(s)=mathbb{E}[G_t|s_t=s] Vπ(s)=E[Gt∣st=s]
-
G t = r t + γ r t + 1 + γ 2 r t + 2 + r 3 γ r t + 3 + . . . G_t = r_t+gamma r_{t+1}+gamma^2r_{t+2}+r^3gamma r_{t+3}+... Gt=rt+γrt+1+γ2rt+2+r3γrt+3+... in MDP M under policy π pi π
-
动态规划
- V π ( s ) ≈ E π [ r t + γ V k − 1 ∣ s t = s ] V^pi(s)approxmathbb{E}_pi[r_t+gamma V_{k-1}|s_t = s] Vπ(s)≈Eπ[rt+γVk−1∣st=s]
- 需要MDP模型M
- 使用估计值bootstraps未来回报
wikipedia: Bootstrapping is a resampling technique used to obtain estimates of summary statistics.
这里引入新的内容
- 如果我们不知道动态模型P/或奖励模型R呢?
- 新内容:在没有模型的条件下进行策略价值评估
- 给定数据/或与环境交互的能力
- 足够计算策略 π pi π的合理估计
Monte Carlo(MC) Policy Evaluation
蒙特·卡罗尔策略评估
- G t = r t + γ r t + 1 + γ 2 r t + 2 + r 3 γ r t + 3 + . . . G_t = r_t+gamma r_{t+1}+gamma^2r_{t+2}+r^3gamma r_{t+3}+... Gt=rt+γrt+1+γ2rt+2+r3γrt+3+... in MDP M under policy π pi π
-
V
π
(
s
)
=
E
T
∼
π
[
G
t
∣
s
t
=
s
]
V^pi(s)=mathbb{E}_{Tau sim pi}[G_t|s_t=s]
Vπ(s)=ET∼π[Gt∣st=s]
- 遵循策略 π pi π产生的迹(trajectories) T Tau T(希腊字母tau)上的期望
迹(trajectories)想表达的是执行路径的意思,其实也可以翻译成路径,但形式化领域惯用迹这种说法。
-
简单的理解思路:价值 = 回报的平均(Value = mean return)
-
如果所有的迹都是有限的,那么我们在迹的集合中采样并计算平均回报
-
不需要MDP的动态模型/回报模型
-
不需要bootstrapping
-
不需要假设状态是马尔科夫的
-
只能被应用于周期化(可以重复进行多次的意思)的MDPs
- 在一个完整的一轮(episode)中取平均
- 需要每一轮都能终止
Monte Carlo(MC) Policy Evaluation
- 目标:在策略
π
pi
π下给定的所有轮次下估计
V
π
V^pi
Vπ
- s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , . . . s_1,a_1,r_1,s_2,a_2,r_2,... s1,a1,r1,s2,a2,r2,...其中的动作都是在策略 π pi π中采样得到的。
- G t = r t + γ r t + 1 + γ 2 r t + 2 + γ 3 r t + 3 + . . . G_t=r_t+gamma r_{t+1}+gamma^2r_{t+2}+gamma^3r_{t+3}+... Gt=rt+γrt+1+γ2rt+2+γ3rt+3+... in MDP M under policy π pi π
- V π ( s ) = E π [ G t ∣ s t = s ] V^pi(s) = mathbb{E}_pi[G_t|s_t=s] Vπ(s)=Eπ[Gt∣st=s]
- MC计算实验平均回报
- 通常是通过一个递增的风格实现的
- 在每一轮之后,更新 V π V^pi Vπ的估计
First-Visit Monte Carlo(MC) On Policy Evaluation Algorithm
Initialize
N
(
s
)
=
0
N(s) = 0
N(s)=0,
G
(
s
)
=
0
∀
s
∈
S
G(s)=0 forall s in S
G(s)=0 ∀s∈S
Loop
- Sample episode i = s i , 1 , a i , 1 , r i , 1 , s i , 2 , a i , 2 , r i , 2 , . . . , s i , T i i=s_{i,1},a_{i,1},r_{i,1},s_{i,2},a_{i,2},r_{i,2},...,s_{i,Tau_i} i=si,1,ai,1,ri,1,si,2,ai,2,ri,2,...,si,Ti
- Define G i , t = r i , t + γ r i , t + 1 + γ 2 r i , t + 2 + . . . + γ T i − 1 r i , τ i G_{i,t}=r_{i,t}+gamma r_{i, t+1} + gamma^2r_{i, t+2}+...+gamma^{Tau_i-1}r_{i, au_i} Gi,t=ri,t+γri,t+1+γ2ri,t+2+...+γTi−1ri,τi as return from time step t onwards in ith episode
- For each state s visited in episode i
- For first time t that state s is visited in episode i
- Increment counter of total first visits: N ( s ) = N ( s ) + 1 N(s) = N(s)+1 N(s)=N(s)+1
- Increment total return G ( s ) = G ( s ) + G i , t G(s)=G(s)+G_{i,t} G(s)=G(s)+Gi,t
- Update estimate V π ( s ) = G ( s ) / N ( s ) V_pi(s) = G(s)/N(s) Vπ(s)=G(s)/N(s)
- For first time t that state s is visited in episode i
Bias, Variance and MSE
深度学习的概率基础,这里复习一下,因为要衡量估计的好坏,不懂的话参见深度学习那本花书。
- 考虑一个被 θ heta θ参数化的统计模型,它决定了在观测数据上的概率分布 P ( x ∣ θ ) P(x| heta) P(x∣θ)
- 考虑一个统计
θ
^
hat{ heta}
θ^,它提供了
θ
heta
θ的一个估计并且它是观测数据x上的一个函数
- 比如。对于一个未知方差的高斯分布,独立同分布(iid,independently identically distribution) 数据点的平均值是对高斯分布平均的一个估计
- 定义:估计
θ
^
hat{ heta}
θ^的bias是:
B i a s θ ( θ ^ ) = E x ∣ θ [ θ ^ ] − θ Bias_ heta(hat{ heta})=mathbb{E}_{x| heta}[hat{ heta}]- heta Biasθ(θ^)=Ex∣θ[θ^]−θ - 定义:估计
θ
^
hat{ heta}
θ^的Variance是:
V a r ( θ ^ ) = E x ∣ θ [ ( θ ^ − E [ θ ^ ] ) 2 ] Var(hat{ heta})=mathbb{E}_{x| heta}[(hat{ heta}-mathbb{E}[hat{ heta}])^2] Var(θ^)=Ex∣θ[(θ^−E[θ^])2] - 定义:估计
θ
^
hat{ heta}
θ^的均方误差(MSE)是:
M S E ( θ ^ ) = V a r ( θ ^ ) + B i a s ( θ ^ ) 2 MSE(hat{ heta})=Var(hat{ heta})+Bias(hat{ heta})^2 MSE(θ^)=Var(θ^)+Bias(θ^)2
M S E ( θ ^ ) = E x ∣ θ [ ( ^ θ ) − θ ] 2 MSE(hat{ heta})=mathbb{E}_{x| heta}[hat( heta)- heta]^2 MSE(θ^)=Ex∣θ[(^θ)−θ]2 (按MSE的定义,博主补充的公式)
有了补充的知识后,在回头看上面的算法:

它有如下性质:
- V π V^pi Vπ估计器是真实期望 E π [ G t ∣ s t = s ] mathbb{E}_pi[G_t|s_t=s] Eπ[Gt∣st=s]的一个无偏估计器
- 根据大数定理,当 N ( s ) → ∞ N(s) ightarrow infty N(s)→∞时, V π ( s ) → E π [ G t ∣ s t = t ] V^pi(s) ightarrow mathbb{E}_pi[G_t|s_t=t] Vπ(s)→Eπ[Gt∣st=t]
Concentration inqualities通常用于Variance。通常我们不知道确切的Bias,除非知道ground truth值。实践中有很多方法得到bias的估计:比较不同形式的参数模型、structural risk maximization。
Every-Visit Monte Carlo (MC) On Policy Evaluation Algorithm
Initialize
N
(
s
)
=
0
N(s) = 0
N(s)=0,
G
(
s
)
=
0
∀
s
∈
S
G(s)=0 forall s in S
G(s)=0 ∀s∈S
Loop
- Sample episode i = s i , 1 , a i , 1 , r i , 1 , s i , 2 , a i , 2 , r i , 2 , . . . , s i , T i i=s_{i,1},a_{i,1},r_{i,1},s_{i,2},a_{i,2},r_{i,2},...,s_{i,Tau_i} i=si,1,ai,1,ri,1,si,2,ai,2,ri,2,...,si,Ti
- Define G i , t = r i , t + γ r i , t + 1 + γ 2 r i , t + 2 + . . . + γ T i − 1 r i , τ i G_{i,t}=r_{i,t}+gamma r_{i, t+1} + gamma^2r_{i, t+2}+...+gamma^{Tau_i-1}r_{i, au_i} Gi,t=ri,t+γri,t+1+γ2ri,t+2+...+γTi−1ri,τi as return from time step t onwards in ith episode
- For each state s visited in episode i
- For every time t that state s is visited in episode i
- Increment counter of total first visits: N ( s ) = N ( s ) + 1 N(s) = N(s)+1 N(s)=N(s)+1
- Increment total return G ( s ) = G ( s ) + G i , t G(s) = G(s) + G_{i,t} G(s)=G(s)+Gi,t
- Update estimate V π ( s ) = G ( s ) / N ( s ) V^pi(s)=G(s)/N(s) Vπ(s)=G(s)/N(s)
- For every time t that state s is visited in episode i
它有如下性质:
- V π V^pi Vπevery-visit MC估计器是真实期望 E π [ G t ∣ s t = s ] mathbb{E}_pi[G_t|s_t=s] Eπ[Gt∣st=s]的一个无偏估计器
- 但是一致性估计器(比如上面的First-Visit)通常会有更好的MSE误差
Incremental Carlo(MC) On Policy Evaluation Algorithm
Initialize
N
(
s
)
=
0
N(s) = 0
N(s)=0,
G
(
s
)
=
0
∀
s
∈
S
G(s)=0 forall s in S
G(s)=0 ∀s∈S
Loop
- Sample episode i = s i , 1 , a i , 1 , r i , 1 , s i , 2 , a i , 2 , r i , 2 , . . . , s i , T i i=s_{i,1},a_{i,1},r_{i,1},s_{i,2},a_{i,2},r_{i,2},...,s_{i,Tau_i} i=si,1,ai,1,ri,1,si,2,ai,2,ri,2,...,si,Ti
- Define G i , t = r i , t + γ r i , t + 1 + γ 2 r i , t + 2 + . . . + γ T i − 1 r i , τ i G_{i,t}=r_{i,t}+gamma r_{i, t+1} + gamma^2r_{i, t+2}+...+gamma^{Tau_i-1}r_{i, au_i} Gi,t=ri,t+γri,t+1+γ2ri,t+2+...+γTi−1ri,τi as return from time step t onwards in ith episode
- For state s visited at time step t in episode i
- Increment counter of total first visits: N ( s ) = N ( s ) + 1 N(s) = N(s)+1 N(s)=N(s)+1
- Update estimate
V π ( s ) = V π ( s ) N ( s ) − 1 N ( s ) + G i , t N ( s ) = V π ( s ) + 1 N ( s ) ( G i , t − V π ( s ) ) V^pi(s)=V^pi(s)frac{N(s)-1}{N(s)}+frac{G_{i,t}}{N(s)}= V^pi(s)+frac{1}{N(s)}(G_{i,t}-V^pi(s)) Vπ(s)=Vπ(s)N(s)N(s)−1+N(s)Gi,t=Vπ(s)+N(s)1(Gi,t−Vπ(s))
注意比较前面以及上面以及下面算法的区别,没有了every-visit,变成了时间步t,即更新条件在不断改变,除此之外也在不断改变Update estimate的内容。
Incremental Carlo(MC) On Policy Evaluation Algorithm, Running Mean
Initialize
N
(
s
)
=
0
N(s) = 0
N(s)=0,
G
(
s
)
=
0
∀
s
∈
S
G(s)=0 forall s in S
G(s)=0 ∀s∈S
Loop
-
Sample episode i = s i , 1 , a i , 1 , r i , 1 , s i , 2 , a i , 2 , r i , 2 , . . . , s i , T i i=s_{i,1},a_{i,1},r_{i,1},s_{i,2},a_{i,2},r_{i,2},...,s_{i,Tau_i} i=si,1,ai,1,ri,1,si,2,ai,2,ri,2,...,si,Ti
-
Define G i , t = r i , t + γ r i , t + 1 + γ 2 r i , t + 2 + . . . + γ T i − 1 r i , τ i G_{i,t}=r_{i,t}+gamma r_{i, t+1} + gamma^2r_{i, t+2}+...+gamma^{Tau_i-1}r_{i, au_i} Gi,t=ri,t+γri,t+1+γ2ri,t+2+...+γTi−1ri,τi as return from time step t onwards in ith episode
-
For state s visited at time step t in episode i
- For state s is visited at time step t in episode i
- Increment counter of total first visits: N ( s ) = N ( s ) + 1 N(s) = N(s)+1 N(s)=N(s)+1
- Update estimate
V π ( s ) = V π ( s ) + α ( G i , t − V π ( s ) ) V^pi(s)=V^pi(s)+alpha(G_{i,t}-V^pi(s)) Vπ(s)=Vπ(s)+α(Gi,t−Vπ(s))
- For state s is visited at time step t in episode i
-
α = 1 N ( s ) alpha=frac{1}{N(s)} α=N(s)1时,和every-visit MC算法等同
-
α > 1 N ( s ) alpha>frac{1}{N(s)} α>N(s)1时,算法会忘掉旧数据,在non-stationary(非固定)领域非常有用
举一个例子,新闻推荐系统中,新闻是在不断变化着的,因此大家通常会重新训练以应对非固定过程(non-stationary)。
例题


Q1: V s 1 = V s 2 = V s 3 = 1 V_{s_1} = V_{s_2} = V_{s_3}=1 Vs1=Vs2=Vs3=1, V s 4 = V s 5 = V s 6 = V s 7 = 0 V_{s_4}=V_{s_5}=V_{s_6}=V_{s_7}=0 Vs4=Vs5=Vs6=Vs7=0
为什么只有在 s 1 s_1 s1有回报1,其余都没有回报,但价值却是1呢。因为算法在整个轮次结束,最后一次更新V,这时候 G = 1 G=1 G=1,只有 s 1 s_1 s1、 s 2 s_2 s2、 s 3 s_3 s3三个状态被访问过,又因为使用的是First-Vist算法,所以,它们count都是1,那么 1 1 = 1 frac{1}{1}=1 11=1
Q2: V s 2 = 1 V_{s_2}=1 Vs2=1
为什么,因为现在是Every-Visit,所以 s 2 s_2 s2的count是2,所以 2 2 = 1 frac{2}{2}=1 22=1。
MC Policy Evaluation 图片概括描述
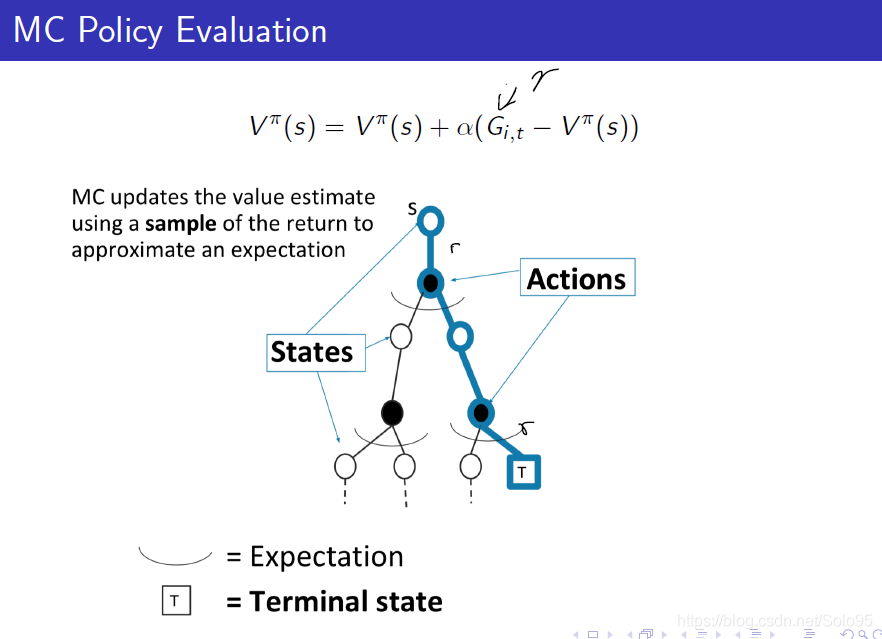
MC通过在整个迹上取近似平均(期望)来更新价值估计。
Monte Carlo (MC) Policy Evaluation Key Limitations
- 通常是个高方差估计器
- 降低这些方差需要大量数据
- 要求必须是可重复情景
- 一个轮次在该轮次的数据用于更新价值函数前该伦次必须能结束
Monte Carlo (MC) Policy Evaluation Summary
- 目标:在给定由于遵循策略
π
pi
π而产生的所有轮次的条件下估计
V
π
(
s
)
V^pi(s)
Vπ(s)
- s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , . . . s_1,a_1,r_1,s_2,a_2,r_2,... s1,a1,r1,s2,a2,r2,...其中动作a在策略 π pi π下采样而来
- MDP M在遵循策略 π pi π G t = r t + γ t t + 1 + γ 2 r t + 2 + γ 3 r t + 3 + . . . G_t=r_t+gamma t_{t+1}+gamma^2r_{t+2}+gamma^3r_{t+3}+... Gt=rt+γtt+1+γ2rt+2+γ3rt+3+...
- V π ( s ) = E π [ G t ∣ s t = s ] V^pi(s)=mathbb{E}_pi[G_t|s_t=s] Vπ(s)=Eπ[Gt∣st=s]
- 简单理解:依靠实验平均来估计期望(给定从我们所关心策略中采样得到的所有轮次)或者重新加权平均(Importance Sampling,即重要性采样)
- 更新价值估计是依靠使用一次回报的采样对期望进行近似
- 不使用bootstrapping
- 在某些假设(通常是温和假设)下收敛到真实值
Temporal Difference(TD)
时序差分
“if one had to identify one idea as central and novel to reinforcement learning, it would undoubtedly be temporal-difference(TD) learning.” - Sutton and Barto 2017
- 如果要选出对强化学习来说是最核心且最新颖的思想,那好毫无疑问是时序差分学习。-Sutton and Barto 2017
- 它结合了蒙特·卡罗尔(策略评估)方法和动态规划方法
- 不依赖模型
- Boostraps和samples(采样)都进行
Bootstrapping通常被用于近似未来回报的折扣总和;Sampling通常被用于近似所有状态上的期望。 - 在可重复进行和非有限horizon非重复情境下都可以使用(这说明它解决了动态规划和蒙特·卡罗尔方法的缺点,博主注)
- 在每一次 ( s , a , r , s ′ ) (s,a,r,s') (s,a,r,s′)四元组(即每一次状态变迁/每一次Observation)发生后都立即更新 V V V的估计
Temporal Difference Learning for Estimating V
- 目标:在给定由于遵循策略 π pi π而产生的所有轮次的条件下估计 V π ( s ) V^pi(s) Vπ(s) (同上)
- MDP M在遵循策略 π pi π G t = r t + γ t t + 1 + γ 2 r t + 2 + γ 3 r t + 3 + . . . G_t=r_t+gamma t_{t+1}+gamma^2r_{t+2}+gamma^3r_{t+3}+... Gt=rt+γtt+1+γ2rt+2+γ3rt+3+... (同上)
- V π ( s ) = E π [ G t ∣ s t = s ] V^pi(s)=mathbb{E}_pi[G_t|s_t=s] Vπ(s)=Eπ[Gt∣st=s]
- 重温Bellman operator (如果MDP模型已知)
B π V ( s ) = r ( s , π ( s ) ) + γ ∑ s ′ ∈ S p ( s ′ ∣ s , π ( s ) ) V ( s ′ ) B^pi V(s)=r(s,pi(s))+gamma sum_{s' in S}p(s'|s,pi(s))V(s') BπV(s)=r(s,π(s))+γs′∈S∑p(s′∣s,π(s))V(s′) - 递增every-visit MC算法,使用一次对回报的采样更新估计
V π ( s ) = V π ( s ) + α ( G i , t − V π ( s ) ) V^pi(s) = V^pi(s)+alpha(G_{i, t}-V^pi(s)) Vπ(s)=Vπ(s)+α(Gi,t−Vπ(s)) - 灵感:已经有一个
V
π
V^pi
Vπ的估计器,使用下面的方法估计回报的期望
V π ( s ) = V π ( s ) + α ( [ r t + γ V π ( s t + 1 ) ] − V π ( s ) ) Vpi(s) = Vpi(s) + alpha([r_t+gamma V^pi(s_{t+1})]-V^pi(s)) Vπ(s)=Vπ(s)+α([rt+γVπ(st+1)]−Vπ(s))
Temporal Difference [TD(0)] Learning
时序差分学习
- 目标:在给定由于遵循策略
π
pi
π而产生的所有轮次的条件下估计
V
π
(
s
)
V^pi(s)
Vπ(s) (同上)
- s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , . . . s_1,a_1,r_1,s_2,a_2,r_2,... s1,a1,r1,s2,a2,r2,...其中动作a在策略 π pi π下采样而来
- 最简单的采样TD学习:以趋近估计值的方式更新价值
V π ( s t ) = V π ( s t ) + α ( [ r t + γ V π ( s t + 1 ) ] − V π ( s t ) ) V^pi(s_t)=V^pi(s_t)+alpha([r_t+gamma V^pi(s_{t+1})]-V^pi(s_t)) Vπ(st)=Vπ(st)+α([rt+γVπ(st+1)]−Vπ(st))
TD target = [ r t + γ V π ( s t + 1 ) ] [r_t+gamma V^pi(s_{t+1})] [rt+γVπ(st+1)]
请注意,这里没有求和,我们是采样,所以上面的式子里只有一个下一个状态,而不是所有的未来状态。而且像动态规划那样,我们会使用先前的 V π V^pi Vπ估计。所以你可以把式子左边的 V π ( s t ) V^pi(s_t) Vπ(st)写成 V k + 1 π ( s t ) V_{k+1}^pi(s_t) Vk+1π(st),右边的 V π ( s t ) V^pi(s_t) Vπ(st)写成 V k π ( s t ) V_{k}^pi(s_t) Vkπ(st)。和动态规划的区别在于,动态规划相当于更新了整个价值函数,这里相当于仅更新了价值函数的一个项。 - TD error:
δ t = r t + γ V π ( s t + 1 ) − V π ( s t ) delta_t = r_t + gamma V^pi(s_{t+1})-V^pi(s_t) δt=rt+γVπ(st+1)−Vπ(st)
V π ( s t ) ≈ V^pi(s_t) approx Vπ(st)≈下一个状态 s ′ s' s′上的期望 - 可以在一次状态变迁(s,a,r,s’)发生后立即更新价值估计
- 不要求必须是可重复情景
Temporal Difference [TD(0)] Learning Algorithm
Input:
α
alpha
α
Initialize
V
π
=
0
,
∀
s
∈
S
V^pi=0, forall s in S
Vπ=0,∀s∈S
Loop
- Sample tuple ( s t , a t , r t , s t + 1 ) (s_t, a_t, r_t, s_{t+1}) (st,at,rt,st+1)
-
V
π
(
s
t
)
=
V
π
(
s
t
)
+
α
(
[
r
t
+
γ
V
π
(
s
t
+
1
]
−
V
π
(
s
t
)
)
V^pi(s_t)=V^pi(s_t) + alpha([r_t+gamma V^pi(s_{t+1}]-V^pi(s_t))
Vπ(st)=Vπ(st)+α([rt+γVπ(st+1]−Vπ(st))
TD target = [ r t + γ V π ( s t + 1 ) ] [r_t+gamma V^pi(s_{t+1})] [rt+γVπ(st+1)]
α alpha α可以是一个时间的函数, a t a_t at是 π ( s t ) pi(s_t) π(st),因为遵循策略 π pi π。
例题

手写体是解题过程。
与蒙特·卡罗尔算法不同的是,我们不会再将回报反向传播到之前访问过的状态,而是采样一个四元组
(
s
,
a
,
r
,
s
′
)
(s,a,r,s')
(s,a,r,s′)即一次变迁,更新
V
(
s
)
V(s)
V(s)的状态,之后不记录这次采样,也不会再改变
s
s
s的价值
V
(
s
)
V(s)
V(s)。
结果是按照手写体以如下顺序生成的(初始化所有状态的价值为零):
- [0 0 0 0 0 0 0]
- [0 0 0 0 0 0 0]
- [0 0 0 0 0 0 0]
- [1 0 0 0 0 0 0]
最后一次采样得到 ( s 1 , a 1 , 1 , # ) (s_1,a_1,1,#) (s1,a1,1,#),按照TD[(0)]算法更新步骤算, V ( s 1 ) = 1 V(s_1) = 1 V(s1)=1,其余由于更新它们价值时回报都是0,所以 V ( s ) = 0 ( e x c e p t f o r s 1 ) V(s)=0(except for s_1) V(s)=0(except for s1)。
TD Learning和Q-Learing高度相似。Q-Learning是在做对模型的控制,即求解最佳策略;TD-Learning基本上就是Q-Learning,但是你的策略是固定的。
实际中如果你取 α = 1 N alpha=frac{1}{N} α=N1或者其他类似的形式,或者取一个很小的值,那么它将必定收敛,当你像上面的例题那样取 α = 1 alpha=1 α=1,它绝对会震荡。 α = 1 alpha=1 α=1其实意味着你直接忽视掉了先前的估计。
图形化描述
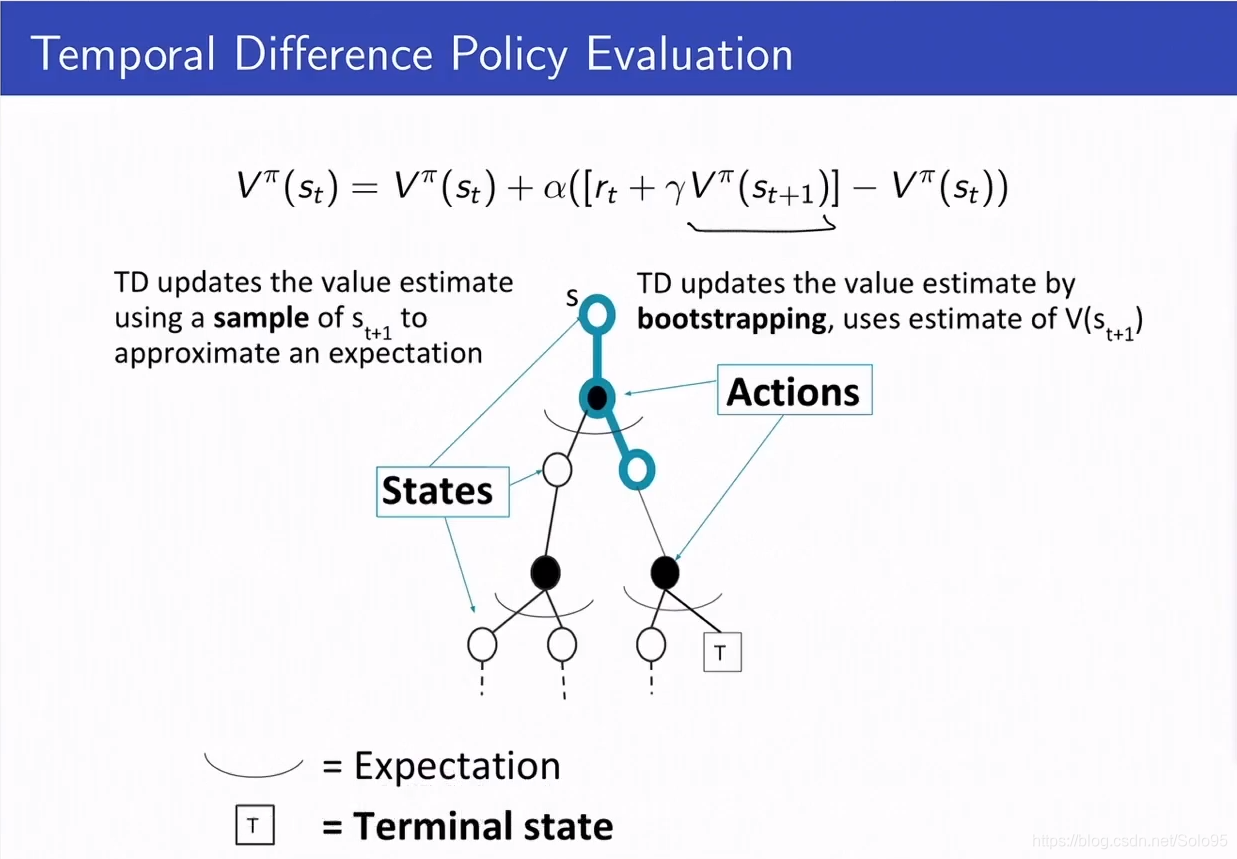
TD是蒙特·卡罗尔和动态规划的结合。因为,一方面它靠采样
s
t
+
1
s_{t+1}
st+1来近似期望,而不是显式地求期望(蒙特·卡罗尔方法的思想);另一方面它使用
V
(
s
t
+
1
)
V(s_{t+1})
V(st+1)通过bootstrap的方式更新价值估计(动态规划的思想)。
总结:动态规划(DP)、蒙特·卡罗尔(MC)、时序差分(TD)
DP、MC、TD三种算法符合下面哪些性质?

- 在没有当前域的模型的情况下依然可用
MC和TD。
MC、TD 都是依靠采样,MC采样整个轮次,TD采样下一个状态,它们都不依赖模型。
- 能处理连续(continuing)(non-episodic不可重复)域
DP和TD。
或者可以说整个过程不会终止 。
MC采样整个轮次,而整个学习过程是不终止的,也就无法采集到整个轮次的数据,所以MC自然不能应用在该场景。
- 能处理非马尔科夫域
只有MC。
TD和DP都要求当前状态的价值不依赖于历史,它们都在当前状态bootstrap,忽略掉了历史状态。MC仅仅对当前状态到本轮终止的回报做了求和,这要求你要抵达计算的那个特定的当前状态,因此回报可能是不同的,它可能会依赖历史(历史决定了你会抵达哪个当前状态)。所以MC不依赖整个world必须是马尔科夫的。
TD和DP在定义时就假定了world是马尔科夫的,bootstrap这样方式就是基于对当前状态,我的未来价值的预测仅仅取决于当前状态。所以可以用得到即时回报再加上变迁到的任何状态的回报作为估计,这已经是历史的充分统计并且可以插入bootstrap估计器。所以它们依赖马尔科夫假设。
因为它们是算法,所以你依然能把应用到非马尔科夫域,但是它们不会在极限下收敛到正确的值。
在极限条件下收敛到真实值(For tabular representations of value function)
在满足三种算法的应用条件下,它们都能收敛到真实值。
对价值的估计是无偏的
- MC是无偏估计,因为它采样真实值然后计算,所以当然没有bias。
- First-Visit是unbais的,Every-Visit是bais的(不是真实值了)。
- TD有偏估计,原因你可以再看一遍TD描述。
- DP很奇怪,询问DP是否是无偏的是一个不公平的问题。DP永远会给你当前策略下确切的 V k − 1 V_{k-1} Vk−1值。
如何选择这些算法?
- Bias/Variance特性
- 数据高效性
- 计算高效性

Batch MC and TD
如果我们想多次利用我们的数据,意即想使用更大的计算量,使得我们能够得到更好的估计并且采样更高效。即更高效利用数据以得到更好的估计。
- Batch (Offline) solution for finite dataset
- Given set of K episodes
- Repeatedly sample an episode from K
- Apply MC or TD(0) to the sampled episode
- What do MC and TD(0) converge to ?
尽可能多次的利用数据去得到更好的数据。
有这样的一个简单例子,只有A,B两个状态,设
γ
=
1
gamma=1
γ=1,给定8轮采样的结果,求TD和MC下的V(A)和V(B)?

V(B) = 0.75 in both TD and MC.
V(A) = 0 in MC, 因为只有迹
A
,
0
,
B
,
0
A,0,B,0
A,0,B,0 中有状态A, 而且从A开始到结束的回报是0。
V(A) = 0.75 in TD,因为V(B) = 0.75,B是A的下一个状态,bootstrap的时候将A更新为0.75,当然,这需要
α
=
1
alpha=1
α=1。
Batch MC and TD: Converges
- 批处理设置的蒙特·卡罗尔方法收敛到最小MSE(mean squared error)。
- 对观察到的回报而言是最小的loss。
- 在AB例题中,V(A)=0
- 批处理的TD(0)收敛到最大似然模型估计MPD的DP策略
V
π
V^pi
Vπ。
- 最大似然马尔科夫决策过程模型

使用这个模型计算 V π V^pi Vπ
在AB例题中,V(A)=0.75
- 最大似然马尔科夫决策过程模型
无模型的策略评估算法重要特性
- 数据高效性 & 计算高效性
- 在最简单的TD,使用一次
(
s
,
a
,
r
,
s
′
)
(s,a,r,s')
(s,a,r,s′)去更新
V
(
s
)
V(s)
V(s)
- 每一次更新操作O(1)
- 一轮的长度是L,O(L)
- 在MC,需要等到整个轮次结束,所以也是O(L)
- MC相较于TD来讲数据高效性更好
- 但是TD可以利用马尔科夫结构
- 如果实在马尔科夫域,这种利用是非常有帮助的
Alternative: Certainty Equivalence V π V^pi Vπ MLE MDP Model Estimate
补充的数据高效性比前面所有方法都要高的方法。
