二分图匹配详解

1.二分图的原始模型及相关概念

二分图又称作二部图，是图论中的一种特殊模型。
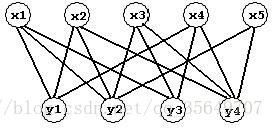
设G=(V,E)G=(V,E)是一个无向图。如顶点集VV 可分割为两个互不相交的子集，并且图中每
条边依附的两个顶点都分属两个不同的子集。则称图GG 为二分图。我们将上边顶点集合称
为XX 集合，下边顶点结合称为YY 集合，如下图，就是一个二分图。

给定一个二分图G(无向图)，在G的一个子图M中，M的边集中的任意两条边都不依附于同一个顶点，则称M是一个匹配.

       选择这样的边数最大的子集称为图的最大匹配问题（maximal matchingproblem)

       如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。

       如果该二分图的每条边都有一个权值且存在完备匹配，那么我们要找出一个所有边权值和最大的完备匹配的问题叫做二分图的最优匹配问题。

二分图的最小覆盖数：

在二分图中选取最少数目的点集，使得二分图任意一边都至少有一个端点在该点集中。这个点集的大小是二分图的最小覆盖数，且二分图的最小覆盖数==二分图的最大匹配数。

二分图的最大独立集：

在二分图中选取最多数目的点集，使得该点集中的任意两点在二分图中都不存在一条边相连。这个点集就是二分图的最大独立集。且二分图的最大独立集大小==|G|(二分图顶点数) - 二分图最大匹配数。

 DAG的最小路径覆盖：

即在DAG图中寻找尽量少的路径，使得每个节点恰好在一条路径上(不同的路径不可能有公共点)。注意：单独的节点也可以作为一条路径。

DAG最小路径覆盖解法如下：

把所有节点i拆为左边点集的i和右边点集的i’，如果DAG图中有i到j的有向边，那么添加一条二分图的i到j’的无向边。最终DAG的最小路径覆盖数==DAG图的节点数n - 新二分图的最大匹配数m。注意：该由原DAG图构建的新二分图的最大匹配数m<=n-1.

有向图是否存在有向环覆盖？把有向图的所有节点i拆为左边点集的i和右边点集的i’，如果有向图中有i到j的有向边，那么添加一条二分图的i到j’的无向边。最终如果新二分图的最大匹配数m==有向图的节点数n，那么说明该有向图的所有节点能被正好1个或多个不相交(没有公共节点)的有向环覆盖。

       原理类似于DAG的最小路径覆盖的解释，因为每个节点都能找到一个后继节点继续往下一直走，所以必然原来有向图存在环。又因为在一个可行的最大匹配中，每个节点只有一个后继，所以必然存在不相交的有向环覆盖。

       有向图的最优有向环覆盖：在有向图中找到1个或多个点不想交的环，这些环正好覆盖了有向图的所有节点且这些环上边的权值最大。本问题解法：把有向图的所有节点i拆为左边点集的i和右边点集的i’，如果有向图中有i到j的有向边，那么添加一条二分图的i到j’的无向边。最终计算二分图的最优完美匹配即可，该二分图的最优完美匹配的权值和就是有向图的最优有向环覆盖的权值和。

2.求解二分图最大匹配

网络流算法
使用网络流算法：
实际上，可以将二分图最大匹配问题看成是最大流问题的一种特殊情况。
用网络流算法思想解决最大匹配问题的思路：
首先：建立源点ss 和汇点tt ，从ss 向XX 集合的所有顶点引一条边，容量为11，从YY 集合
的所有顶点向TT 引一条边，容量为11。
然后：将二分图的所有边看成是从XiXi到YjYj的一条有向边，容量为1。
求最大匹配就是求ss 到tt 的最大流。
最大流图中从XiXi 到YjYj 有流量的边就是匹配集合中的一条边。

匈牙利算法
发现了一篇写得非常好的博客，可以看看这里的解释：趣写算法系列之–匈牙利算法

3.常见模型

上面已经提到了图的匹配的概念，此外还有几个相关的有用的概念，在此我们再介绍除
匹配之外的三个概念：
记图G=(V,E)G=(V,E)。

匹配：在GG 中两两没有公共端点的边集合M⊂EM⊂E。
边覆盖：GG 中的任意顶点都至少是FF 中某条边的端点的边集F⊂EF⊂E。
独立集：在GG 中两两互不相连的顶点集合S⊂VS⊂V。
顶点覆盖：GG 中的任意边都有至少一个端点属于SS 的顶点集合S⊂VS⊂V 。

相应的也有：最大匹配，最小边覆盖，最大独立集，最小顶点覆盖。
例如下图中，最大匹配为{e1,e3}{e1,e3}，最小边覆盖为{e1,e3,e4}{e1,e3,e4}，最大独立集为{v2,v4,v5}{v2,v4,v5}，

三个重要等式：
在二分图中满足：
(1) 对于不存在孤立点的图， 最大匹配 + 最小边覆盖 =VV
证明:通过最大匹配加边得到最小边覆盖。

(2) 最大独立集 +最小顶点覆盖=VV
证明:独立集中若存在边，那么顶点覆盖不能覆盖完所有边，矛盾。

(3)|最大匹配| = |最小顶点覆盖|。
具体证明参考：百度百科:Konig定理
二分图的最小顶点覆盖 最大独立集 最大团

有向图中应用二分匹配
求有向图最小路径覆盖：
对于有向图的最小路径覆盖，先拆点，将每个点分为两个点，左边是1-n个点，右边是1-n个点
然后每一条有向边对应左边的点指向右边的点。对此图求最大匹配，再用n-最大匹配即可。

证明：
将图中顶点看做n条边，每次加入一条有向边相当于合并两条边，又因为一个点只能经过一次，与匹配的性质一样。

例题
POJ3041(求最小点覆盖)

将所有x行视为一个点集，所有y列视为一个点集，那么（x，y）就表示x和y之间有一条边了。而这题所求是最小点覆盖，即最大匹配。

#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
int n,map[510][510],flag[510],vis[510];
int find(int k);
int main()
{
	int i,j,k,sum,m,x,y;
	memset(map,0,sizeof(map));
	memset(flag,0,sizeof(flag));
	scanf("%d%d",&n,&m);
	for(i=1;i<=m;i++)
	{
		scanf("%d%d",&x,&y);
		map[x][y]=1;
	}
	sum=0;
	for(i=1;i<=n;i++)
	{
		memset(vis,0,sizeof(vis));
		if(find(i))
			sum+=1;
	}
	printf("%d
",sum);
	return 0;
}
int find(int k)
{
	int i,j;
	for(j=1;j<=n;j++)
	{
		if(map[k][j] && !vis[j])
		{
			vis[j]=1;
			if(!flag[j] || find(flag[j]))
			{
				flag[j]=k;
				return 1;
			}
		}
	}
	return 0;
}

POJ1422(有向图最小路径覆盖)

 其实每个伞兵走的就是一条有向的简单路径。我们要求的就是该DAG图的最少可以用多少条简单路径覆盖所有节点且任意两条路径不会有重复的节点。 这就是DAG的最小路径覆盖问题。

 DAG最小路径覆盖问题的解 = 节点数-二分图的最大匹配。

 首先要把DAG中的每个点在二分图的左右点集都保存一遍，然后对于DAG中的边i->j， 那么就在二分图中添加边左i->右j。 之后求该二分图的最大匹配边数即可。

#include<cstdio>
#include<cstring>
#include<vector>
using namespace std;
const int maxn=120+5;
 
struct Max_Match
{
    int n;
    vector<int> g[maxn];
    bool vis[maxn];
    int left[maxn];
 
    void init(int n)
    {
        this->n=n;
        for(int i=1; i<=n; ++i) g[i].clear();
        memset(left,-1,sizeof(left));
    }
 
    bool match(int u)
    {
        for(int i=0;i<g[u].size();++i)
        {
            int v=g[u][i];
            if(!vis[v])
            {
                vis[v]=true;
                if(left[v]==-1 || match(left[v]))
                {
                    left[v]=u;
                    return true;
                }
            }
        }
        return false;
    }
 
    int solve()
    {
        int ans=0;
        for(int i=1; i<=n; ++i)
        {
            memset(vis,0,sizeof(vis));
            if(match(i)) ++ans;
        }
        return ans;
    }
}MM;
 
int main()
{
    int T; scanf("%d",&T);
    while(T--)
    {
        int n,m;
        scanf("%d%d",&n,&m);
        MM.init(n);
        while(m--)
        {
            int u,v;
            scanf("%d%d",&u,&v);
            MM.g[u].push_back(v);
        }
        printf("%d
",n-MM.solve());
    }
    return 0;
}

POJ1486Sorting Slides(判断唯一匹配)

其实就是二分图最大匹配问题.左边点集用幻灯片编号表示,右边点集用数字表示. 如果某个幻灯片i包含了数字j,那么从左边i到右边j就存在一条边.

       首先我们求出这个图的最大匹配数x, 根据题意这x值一定是等于n(幻灯片数的). 然后我们记录目前求到的最大匹配的各个边.

       我们每次判断最大匹配边集的某条边是否是必需边. 我们只要先删除这条边,如果之后求最大匹配数依然==n,那么这条边不是必需边.如果之后求最大匹配数依然<n,那么这条边是必需边.(做好标记）

#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=26+5;
 
struct Max_Match
{
    int n,m;
    bool g[maxn][maxn];
    bool vis[maxn];
    int left[maxn];
 
    void init(int n)
    {
        this->n=n;
        memset(g,0,sizeof(g));
        memset(left,-1,sizeof(left));
    }
 
    bool match(int u)
    {
        for(int v=1;v<=n;v++)if(g[u][v] && !vis[v])
        {
            vis[v]=true;
            if(left[v]==-1 || match(left[v]))
            {
                left[v]=u;
                return true;
            }
        }
        return false;
    }
 
    int solve()
    {
        int ans=0;
        for(int i=1;i<=n;i++)
        {
            memset(vis,0,sizeof(vis));
            if(match(i)) ans++;
        }
        return ans;
    }
}MM;
 
int xmin[maxn],ymin[maxn],xmax[maxn],ymax[maxn];
struct
{
    int x;  // edge[i].x=x 表示第i个矩形配对的数字 是x;
    bool ok;//标记该边是否是 必需边
}edge[maxn];
 
int main()
{
    int n,kase=0;
    while(scanf("%d",&n)==1&&n)
    {
        MM.init(n);
        memset(edge,0,sizeof(edge));
        for(int i=1;i<=n;i++)
        {
            scanf("%d%d%d%d",&xmin[i],&xmax[i],&ymin[i],&ymax[i]);
        }
        for(int i=1;i<=n;i++)
        {
            int x,y;
            scanf("%d%d",&x,&y);
            for(int j=1;j<=n;j++)
            {
                if(xmin[j]<=x&&x<=xmax[j]&&ymin[j]<=y&&y<=ymax[j])
                    MM.g[j][i]=true;
            }
        }
        MM.solve();
        int edge_num=n;
        for(int i=1;i<=n;i++)
        {
            edge[MM.left[i]].x=i;
            edge[MM.left[i]].ok=true;
        }
        for(int i=1;i<=n;i++)//尝试删除第i条匹配边
        {
            int j=edge[i].x;
            MM.g[i][j]=false;//删除此边
            memset(MM.left,-1,sizeof(MM.left));
            int num = MM.solve();
            if(num == n)//删除边后,匹配数不变
            {
                edge[i].ok=false;
                edge_num--;
            }
            MM.g[i][j]=true;//还原此边
        }
        printf("Heap %d
",++kase);
        if(edge_num==0) printf("none
");
        else
        {
            for(int i=1;i<=n;i++)if(edge[i].ok)
                printf("(%c,%d) ",i-1+'A',edge[i].x);
            printf("
");
        }
        printf("
");
    }
    return 0;
}

poj2724PurifyingMachine(求二分图最小边覆盖)

 也就是给你一些不同的(判重之后)二进制串,每个串可以通过1次操作净化,也可以把两个只有1位不同的串通过1次操作联合净化.要我们求最少的操作次数.

       我们把所有串按其中1的个数和是奇还是偶分成左右两个点集.

对于任意两个串,如果他们只有1位不同,那么就在他们之间连接一条无向边.(这两个串一定分别属于不同的点集)

       由于串的总数是固定的,且一个串可以通过单独净化也可以通过联合净化.而我们向让净化的次数最少,我们自然想联合净化(即一次可以净化两个串)的次数尽量多了. 那么我们最多可以进行多少次联合净化呢? 这个数值==我们建立二分图的最大匹配边数.(想想是不是,因为一个串最多只能被净化一次)

      假设总的不同串有n个,我们建立二分图的最大匹配数(即联合净化最大次数)为ans,那么我们总共需要n-ans次净化即可.(想想为什么)

       当然本题也可以不用把串特意分成左右点集(本程序实现就是用的这种方式：未分左右点集),我们只需要把原图翻倍,然后求翻倍图的最大匹配数ans,最后用n-ans/2即可。

#include<cstdio>
#include<cstring>
#include<vector>
#include<set>
#include<string>
#include<iostream>
using namespace std;
const int maxn=1000+100;
 
struct Max_Match
{
    int n;
    vector<int> g[maxn];
    bool vis[maxn];
    int left[maxn];
 
    void init(int n)
    {
        this->n=n;
        for(int i=1;i<=n;i++) g[i].clear();
        memset(left,-1,sizeof(left));
    }
 
    bool match(int u)
    {
        for(int i=0;i<g[u].size();i++)
        {
            int v=g[u][i];
            if(!vis[v])
            {
                vis[v]=true;
                if(left[v]==-1 || match(left[v]))
                {
                    left[v]=u;
                    return true;
                }
            }
        }
        return false;
    }
 
    int solve()
    {
        int ans=0;
        for(int i=1;i<=n;i++)
        {
            memset(vis,0,sizeof(vis));
            if(match(i)) ++ans;
        }
        return ans;
    }
}MM;
 
struct Node
{
    string s;
    bool link(Node& rhs)//判断两个string是否只相差1位
    {
        int num = 0;
        for(int i=0;i<s.size(); i++)
            if(s[i]!=(rhs.s)[i]) ++num;
        return num==1;
    }
}node[maxn];
 
int main()
{
    int N,M;
    while(scanf("%d%d",&N,&M)==2 && N)
    {
        int num=0;
        set<string> st;//判重string
        for(int i=1;i<=M;i++)
        {
            string s;
            cin>>s;
            if(s.find("*")!=-1)
            {
                int pos=s.find("*");
                string s1(s),s2(s);
                s1[pos]='0';
                s2[pos]='1';
                if(st.find(s1) == st.end())//s1与已有string不重复
                {
                    st.insert(s1);
                    node[++num].s = s1;
                }
                if(st.find(s2) == st.end())//s2与已有string不重复
                {
                    st.insert(s2);
                    node[++num].s = s2;
                }
            }
            else
            {
                if(st.find(s) == st.end())
                {
                    st.insert(s);
                    node[++num].s = s;
                }
            }
        }
 
        MM.init(num);
        for(int i=1;i<=num;i++)
        for(int j=1;j<=num;j++)if(i!=j)
        if(node[i].link(node[j]))
            MM.g[i].push_back(j);
        printf("%d
",num-MM.solve()/2);
    }
    return 0;
}