正余弦定理解三角形的实际应用

前言

上节课：用正余弦定理解三角形，

本节课和上节课的关系：上节课用正余弦定理解三角形，是针对三角形的数学模型来求解；而本节课需要将实际问题先图形化，转化为针对三角形的数学模型来处理的问题，如果这个环节做得好，那么到此问题就完全变成了上一节的问题。

典例剖析

例1要测量电视塔(AB)的高度，在(C)点测得塔顶(A)的仰角是(45°)，在(D)点测得塔顶(A)的仰角是(30°)，并测得水平面上的(∠BCD＝120°)，(CD＝40 m)，则电视塔的高度为__________(m)．

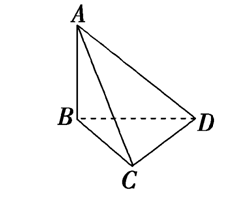
分析：设电视塔(AB)高为(x; m)，

则在(RtDelta ABC)中，由(angle ACB＝45°)得(BC＝x).

在(RtDelta ADB)中，由(angle ADB＝30°)，得(BD＝sqrt{3}x).

在(Delta BDC)中，由余弦定理，得

(BD^2＝BC^2＋CD^2－2BCcdot CDcdot cos120°)，

即((sqrt{3}x)^2＝x^2＋40^2－2cdot xcdot 40cdot cos120°)，

解得(x＝40)，所以电视塔高为(40 m).

反思总结：①解三角形问题时，常常需要将立体问题平面化；②当已知条件不在一个三角形中时，我们常常将其转化到一个三角形中，再求解即可。

例2如图(A、B)两点在河的两侧，且(A、B)两点均不可到达，如果要测量(AB)的距离，测量者在河岸边选定了两点(C、D)，并测得(CD=cfrac{sqrt{3}}{2}km)，(angle ACB=alpha=45^{circ})，(angle ACD=eta=60^{circ})，(angle CDB=gamma=30^{circ})，(angle ADB=delta=30^{circ})，求(A、B)两点间的距离。

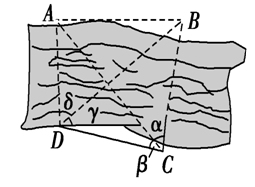
分析：在(Delta ACD)中，由(angle ADC=delta+gamma=60^{circ})，(angle ACD=60^{circ})，(CD=cfrac{sqrt{3}}{2}km)，

可得边(AC=CD=cfrac{sqrt{3}}{2}km)；

在(Delta BCD)中，由(angle BDC=30^{circ})，(angle BCD=105^{circ})，(CD=cfrac{sqrt{3}}{2}km)，

故由正弦定理，可得(BC=cfrac{DC}{sinangle DBC}cdot sinangle BDC=cfrac{sqrt{6}}{4})；

在(Delta ABC)中，由(angle ACB=45^{circ})，(AC=cfrac{sqrt{3}}{2}km)，(BC=cfrac{sqrt{6}}{4})，

由余弦定理可得，(AB^2＝BC^2＋AC^2－2BCcdot ACcdot cos45°)，

解得(AB=cfrac{sqrt{6}}{4}km)

反思总结：1、怎么分析？由果溯因，题目要求解(AB)的长度，需要将其放置到一个三角形中，图中能包纳(AB)在内的三角形有三个，分别是(Delta ABC)和(Delta ABD)和(Delta AOB)，首先能排除的是不选(Delta AOB)，原因是已知条件都用不上。接下来，选择的这两个三角形，从已知数据的角度看是对称的，所以随便选一个，比如(Delta ABC)。在此三角形中，(angle ACB=45^{circ})能用上，自然还得知道边(AC)和(BC)，要求解边(AC)，也得选个三角形，比如选(Delta ACD)，用正弦定理求解(AC)即可；要求解边(BC)，也得选个三角形，比如选(Delta BCD)，用余弦定理求解(BC)即可；到此，回到(Delta ABC)中，用余弦定理就可以搞定问题了。

2、当已知条件转化到一个三角形中时，问题就变得迎刃而解了。

例3如图，在海岸(A)处，发现北偏东(45^{circ})方向距离(A)处((sqrt{3}-1))海里的(B)处有一艘走私船，在(A)处北偏西(75^{circ})方向，距离(A)处(2)海里的(C)处的缉私船奉命以(10sqrt{3})海里/时的速度追截走私船，此时走私船正以(10)海里/时的速度从(B)处向北偏东(30^{circ})方向逃窜，问缉私船沿什么方向能最快追上走私船，并求所需时间。(注：(sqrt{6}approx 2.449))

分析：设缉私船沿北偏东( heta)的(CD)方向能最快追上，所需时间为(t)小时，并设(angle DCB=alpha)，

在(Delta ABC)中，(AB=sqrt{3}-1)，(AC=2)，(angle BAC=120^{circ})，

则由余弦定理可知，(BC^2=AC^2+AB^2-2cdot ACcdot ABcdot cos120^{circ}=cdots=6)，则(BC=sqrt{6})；

在(Delta ABC)中，由正弦定理可知，(cfrac{AC}{sinangle CBA}=cfrac{BC}{sin120^{circ}})，代值整理得到

(sinangle CBA=cfrac{sqrt{2}}{2})，则可知(angle CBA=cfrac{pi}{4})，即(B、C)两点在正东正西方向上。

在(Delta BCD)中，(BC=sqrt{6})，(BD=10t)，(CD=10sqrt{3}t)，(angle CBD=120^{circ})，

则由余弦定理可知，(CD^2=BC^2+BD^2-2cdot BCcdot BDcdot cos120^{circ})，

化简整理得，(200t^2-10sqrt{6}t-6=0)，即((20t+sqrt{6})(10t-sqrt{6})=0)，

解得(t=cfrac{sqrt{6}}{10}approx 0.245)小时(=14.7)分钟。

此时，由正弦定理可得，(cfrac{BD}{sinangle DCB}=cfrac{CD}{sin120^{circ}})，

即(cfrac{10t}{sinalpha}=cfrac{10sqrt{3}t}{sin120^{circ}})，

代值整理得到，(sinalpha=cdots=cfrac{1}{2})，故(alpha=30^{circ})。

即沿北偏东(60^{circ})或东偏北(30^{circ})方向能追上，最快用时约(14.7)分钟。

反思总结：①本题目的难点之一，就是根据题意做出图形，作图时需要理解题中的各种角的含义，②且在(A、B、C)处需要建立方位。同时还存在做出的是俯视图还是斜二测图形。③题目一开始我们并不知道(BC)两点在正东正西方向上，所以直接设沿着东偏北多少是错误的。④在(Delta BCD)中使用正弦定理求(sinangle DCB)时，代入边长时要么都用边长，要么都使用速度，以减少运算错误；如果利用余弦定理计算(cosangle DCB)会非常麻烦。

例4 如图，一条河的两岸平行，河的宽度(d＝0.6 km)，一艘客船从码头A出发匀速驶往河对岸的码头(B)。已知(AB＝1km)，水的流速为(2 km/h)，若客船从码头(A)驶到码头(B)所用的最短时间为(6 min(0.1h))，则客船在静水中的速度为 【 】

$A、8km/h$ $B、6sqrt{2} km/h$ $C、2sqrt{34} km/h$ $D、10 km/h$

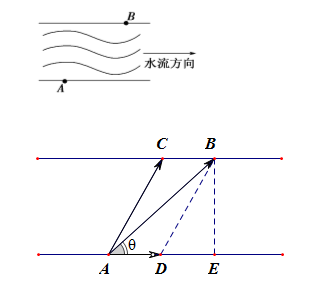
分析：此题涉及到运动的合成，如右图所示，要想使得船的最终实际航行路线是(AB)，那么船在静水中时的航线应该是(AC)，水流的方向是(AD)，这样在两个向量(overrightarrow{AC})、(overrightarrow{AD})的共同作用下，船的最终实际航行路线才可能是(AB)，这样就形成了(Delta ABC)和(Delta ABD)；

设客船在静水中的速度为(v km/h)，那么(AC=BD=0.1v)，(AB=1)，(AD=0.1 imes 2=0.2)，

在(Delta BAE)中，(sin heta=cfrac{0.6}{1}=cfrac{3}{5})，则(cos heta=cfrac{4}{5})，即(cosangle BAD=cos heta=cfrac{4}{5})

则在(Delta ABD)中，(BD^2=AB^2+AD^2-2ABcdot ADcdot cosangle BAD)；

即((0.1v)^2=1^2+(0.2)^2-2 imes 1 imes 0.2 imes cfrac{4}{5})，解得(v=6sqrt{2})，故选(B)。

例5一个大型喷水池的中央有一个强力喷水柱，为了测量喷水柱喷出的水柱的高度，某人在喷水柱正西方向的点(A)测得水柱顶端的仰角为(45^{circ})，沿点A向北偏东(30^{circ})前进(100m)到达点(B)，在(B)点测得水柱顶端的仰角为(30^{circ})，则水柱的高度是【】

$A、50m$ $B、100m$ $C、120m$ $D、150m$

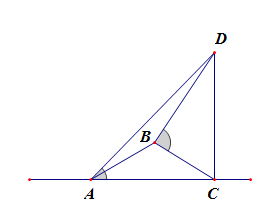
分析：本题目的难点是作出适合题意的立体图形，必要的时候可以使用斜二次画法理解题意。

如右图所示，水柱高为(CD)，其垂直于下底面(ABC)，

(angle DAC=45^{circ})，(angle BAC=60^{circ})，(angle DBC=30^{circ})，

设水柱的高度为(h)，则在(Delta ABC)中，(BC=sqrt{3}h)，(AC=h)，(AB=100)，(angle BAC=60^{circ})，

由余弦定理可得(BC^2=AB^2+AC^2-2ABcdot ACcdot cosangle BAC)，

即(3h^2=h^2+100^2-2 imes 100 imes h imes cfrac{1}{2})，

化简整理得到，(h^2+50h-5000=0)。

解得(h=-100(舍去))或(h=50)。故选(A)。

例6据气象部门预报，在距离某码头正西方向(400km)处的热带风暴中心正以(20km/h)的速度向东北方向移动，距离风暴中心(300km)以内的地区为危险区，该码头处于危险区内的时间是_____小时。

[法1]：解三角形法，设风暴移动的时间为(t)小时， 半径为(300km)的(odot B)代表风暴以及殃及的范围；

则要使得城市不处于危险内，则需要(ABleqslant 300)；若(AB>300)，则此刻城市一定在危险区内；

由题可知，(AB^2=OA^2+OB^2-2 imes OA imes OB imes cos45^{circ})

即(AB^2=400^2+400t^2-2 imes20t imes400cfrac{sqrt{2}}{2})，

令(AB^2leqslant 300^2)，解得(10sqrt{2}-5leqslant t leqslant 10sqrt{2}+5)

即当时间(t=10sqrt{2}-5)时开始，城市进入危险区，当(t=10sqrt{2}+5)时开始，城市脱离危险区，

所以码头处于危险区的时间为(10sqrt{2}+5-(10sqrt{2}-5)=10).

本题目难点：1、转化为解三角形模型；2、(AB^2 leqslant 300^2)的理解；3、解不等式，十字相乘法变换为公式法；4、对(t=10sqrt{2}pm 5)的理解

[法2]：平面几何法，将风暴理解为一个质点，将城市扩大为一个半径为(300km)的圆(odot A)，

则当风暴沿着射线(OD)运动时，城市处于危险区的距离为图中的线段(CD)，

在(Rt riangle OAE)中，容易知道(AE=200sqrt{2})，

则由相交弦定理可知，(DE^2=(300-200sqrt{2}) imes (300+200sqrt{2})=100^2)，

故(DE=100)，(CD=200)，可知风暴作用于码头的距离是(200km)，

故城市处于危险区的时间为(cfrac{200}{20}=10)小时。