一本通【例题4】Addition Chains——题解

又是一道剪枝剪了半天的搜索题。。。题目传送

要充分利用题目中的约束条件：1、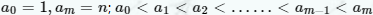；2、对于每个k(1≤k≤m)k(1≤k≤m)满足ak=ai+aj(0≤i,j≤k−1)ak=ai+aj(0≤i,j≤k−1),这里i与j可以相等。由此可以推出a1一定=2(也能减少很多操作次数了吧)

还是先找找搜索过程要面临的状态和有关维度：目标数n,答案序列的长度limit，序列中的每个数ai，当前序列中的最后一个数last。

由于如果不对序列长度加以限制，普通的深搜便会“一发不可收拾”，所以这里用迭代加深搜索。

可行性剪枝考虑：

　　　1、由于迭代加深搜索会把之前的状态全搜索一遍，所以应当限制一下limit的下界。注意到长度为k的序列能最大造出来的数为2^k-1，所以序列最短应保证那个最大造出来的数>=n，预处理就行。

考虑一下搜索顺序：因为n是由小数加小数构造出来的，求最小的构造次数。因此应从大到小搜索。

考虑防等效冗杂：让从大到小枚举的两个数中的第1个正常枚举、第2个从第1个开始枚举。

继续考虑可行性剪枝：

　　　2、当前枚举的序列里的两个数相加应大于last，只有这样才能继续搜索。

　　　3（效率还不够，更近一步考虑一下未来）：发现一个序列最大的增长方式即为让序列中最后一个数自己加自己，设这个数为a，进行k次这样的增长后序列中最后的一个数则为a*2^k，每次增长操作都会增加一个数。对于当前长度为l的序列，如果last*2^limit-l仍小于n，就回溯；等于n，那limit一定是答案；大于n时才继续搜索。2的幂次方可打表或预处理出。

最优性剪枝：找到答案就停止就行。

AC代码：

#include<iostream>
#include<cstdio>

using namespace std;

int n,a[10000],bj,cankao[1055],mi[20];

void dfs(const int &limit,int k)//要填第k个(k从1开始） 
{
    if(bj) return;
    if(k==limit)
    {
        for(int i=k-2;i>=0;i--)
            for(int j=i;j>=0;j--)
            {
                if(a[i]+a[j]==n)
                {
                    a[k-1]=n;
                    bj=1;
                    return;
                }
            }
    }
    if(a[k-2]*mi[limit-k+1]<=n)//可行性剪枝3 
    {
        if(a[k-2]*mi[limit-k+1]==n) 
        {
            bj=1; 
            for(int j=k-1;j<limit;j++)
            a[j]=a[j-1]*2;
        }
        return;
    }
    for(int i=k-2;i>=0;i--)
    {
      for(int j=i;j>=0;j--)//防等效冗杂 
        if(a[i]+a[j]>a[k-2])
        {
            if(a[i]+a[j]>=n) continue;//可行性剪枝2 
            a[k-1]=a[i]+a[j];
            dfs(limit,k+1);
            if(bj) return;
        }
        else
        {
            if(j==i) return;
            break;
        }
    }    
} 

void work()
{
    bj=0;
    for(int len=cankao[n];len<=n;len++)
    {
        dfs(len,3);
        if(bj) 
        {
            for(int i=0;i<len;i++)
                printf("%d ",a[i]);
            putchar('
');
            return;
        }
    }
}

void init()
{
    int i=1,step=1;
    while(i<=1024)
    {
        cankao[i]=step;
        i*=2;
        step++;
    }
    for(i=1;i<=1000;i++)
        if(!cankao[i])
            cankao[i]=cankao[i-1];//以上为可行性剪枝1 
    i=1,step=1;
    mi[1]=1;
    for(int j=1;j<=20;j++)//2的幂次方的预处理 
    {
        i*=2;
        mi[j]=i;
    }
}

int main()//预处理 
{
    init();
    a[0]=1;a[1]=2;//注意序列下标0开始 
    scanf("%d",&n);
    while(n)
    {
        if(n==1)//处理特殊情况 
        {
            putchar('1');
            putchar('
');
        }
        if(n==2)
            cout<<"1 2
";
        if(n>=3)
        work();
        scanf("%d",&n);
    }
    return 0;
}