洛谷P1077 摆花——题解

题目传送

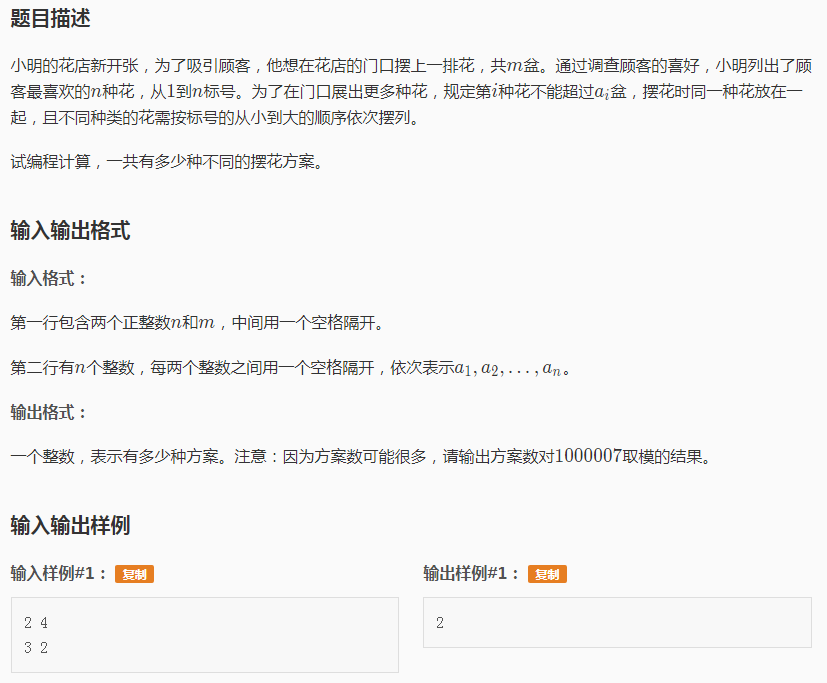
题目大意：有按顺序放的n种花，相同种类的花放一起，每种花最多放ai盆，共放了m盆花，求放花方案数。

求方案个数一般有以下思路：1、搜索；2、递推/动态规划；3、贪心；4、分治。。。

玄学估计发现，仅是可行解就有非常多的数量，显然搜索不行了。联想到“背包问题的方案总数”，猛然发现：这题不就相当于每个物品的重量都为1，最多选a_i个，求放满背包的方案总数吗？尝试写出状态：设dp[k][i]为只可能用前k种花、摆了i盆花的方案数，状态转移方程：(当i大于等于a_k时)dp[k][i]=dp[k-1][i-0]+dp[k-1][i-1]+..+dp[k-1][i-a_k];(当i小于a_k时）dp[k][i]=dp[k-1][i-0]+dp[k-1][i-1]+..+dp[k-1][0]。注意边界条件：a[1][i]=1,i=0，1，...，a₁，即只用第一种花摆花时是不能由上面的状态转移方程推出来的。

见AC代码：

#include<iostream>
#include<cstdio>

using namespace std;

int a[101],n,m,dp[101][101],sum;

const int mod=1000007;

int main()
{
       scanf("%d%d",&n,&m);
       for(int i=1;i<=n;i++)
           scanf("%d",&a[i]);
       for(int i=0;i<=a[1];i++) dp[1][i]=1;//初始化边界条件 
       sum=a[1];
       for(int k=2;k<=n;k++)//花的种类 
       {
           sum+=a[k];
           for(int i=0;i<=sum&&i<=m;i++)//共要摆几个 
           {
               for(int j=0;j<=a[k]&&j<=i;j++)//第k种用几个 
                   dp[k][i]+=dp[k-1][i-j];
            dp[k][i]%=mod;
        }
    }
    cout<<dp[n][m];
    return 0;
}