一、基础理解
- 问题:逻辑回归算法是用回归的方式解决分类的问题,而且只可以解决二分类问题;
- 方案:可以通过改造,使得逻辑回归算法可以解决多分类问题;
- 改造方法:
- OvR(One vs Rest),一对剩余的意思,有时候也称它为 OvA(One vs All);一般使用 OvR,更标准;
- OvO(One vs One),一对一的意思;
- 改造方法不是指针对逻辑回归算法,而是在机器学习领域有通用性,所有二分类的机器学习算法都可使用此方法进行改造,解决多分类问题;
二、原理
1)OvR
- 思想:n 种类型的样本进行分类时,分别取一种样本作为一类,将剩余的所有类型的样本看做另一类,这样就形成了 n 个二分类问题,使用逻辑回归算法对 n 个数据集训练出 n 个模型,将待预测的样本传入这 n 个模型中,所得概率最高的那个模型对应的样本类型即认为是该预测样本的类型;
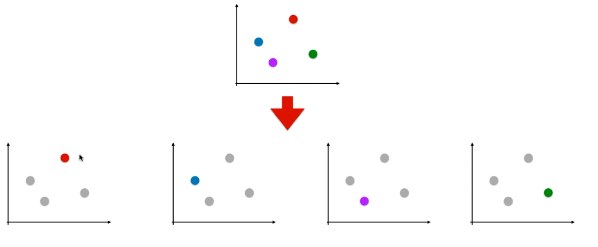
- 时间复杂度:如果处理一个二分类问题用时 T,此方法需要用时 n.T;
2)OvO
- 思想: n 类样本中,每次挑出 2 种类型,两两结合,一共有 Cn2 种二分类情况,使用 Cn2 种模型预测样本类型,有 Cn2 个预测结果,种类最多的那种样本类型,就认为是该样本最终的预测类型;

- 时间复杂度:如果处理一个二分类问题用时 T,此方法需要用时 Cn2 .T = [n.(n - 1) / 2] . T;
3)区别
- OvO 用时较多,但其分类结果更准确,因为每一次二分类时都用真实的类型进行比较,没有混淆其它的类别;
三、scikit-learn 中的逻辑回归
- scikit-learn的LogisticRegression 算法内包含了:正则化、优化损失函数的方法、多分类方法等;
-
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True, intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1, penalty='l2', random_state=None, solver='liblinear', tol=0.0001, verbose=0, warm_start=False)
# LogisticRegression() 实例对象,包含了很多参数;
-
不懂的要学会 看文档、看文档、看文档:help(算法、实例对象);
-
C=1.0:正则化的超参数,默认为 1.0;
- multi_class='ovr':scikit-learn中的逻辑回归默认支持多分类问题,分类方式为 'OvR';
- solver='liblinear'、'lbfgs'、'sag'、'newton-cg':scikit-learn中优化损失函数的方法,不是梯度下降法;
- 多分类中使用 multinomial (OvO)时,只能使用 'lbfgs'、'sag'、'newton-cg' 来优化损失函数;
- 当损失函数使用了 L2 正则项时,优化方法只能使用 'lbfgs'、'sag'、'newton-cg';
- 使用 'liblinear' 优化损失函数时,正则项可以为 L1 和 L2 ;
1)例(3 种样本类型):LogisticRegression() 默认使用 OvR
-
import numpy as np import matplotlib.pyplot as plt from sklearn import datasets iris = datasets.load_iris() # [:, :2]:所有行,0、1 列,不包含 2 列; X = iris.data[:,:2] y = iris.target from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666) from sklearn.linear_model import LogisticRegression log_reg = LogisticRegression() log_reg.fit(X_train, y_train) log_reg.score(X_test, y_test) # 准确率:0.6578947368421053
- 绘制决策边界
def plot_decision_boundary(model, axis): x0, x1 = np.meshgrid( np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1,1), np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1,1) ) X_new = np.c_[x0.ravel(), x1.ravel()] y_predict = model.predict(X_new) zz = y_predict.reshape(x0.shape) from matplotlib.colors import ListedColormap custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9']) plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap) plot_decision_boundary(log_reg, axis=[4, 8.5, 1.5, 4.5]) # 可视化时只能在同一个二维平面内体现两种特征; plt.scatter(X[y==0, 0], X[y==0, 1]) plt.scatter(X[y==1, 0], X[y==1, 1]) plt.scatter(X[y==2, 0], X[y==2, 1]) plt.show()

2)使用 OvO 分类
-
log_reg2 = LogisticRegression(multi_class='multinomial', solver='newton-cg') # 'multinomial':指 OvO 方法; log_reg2.fit(X_train, y_train) log_reg2.score(X_test, y_test) # 准确率:0.7894736842105263 plot_decision_boundary(log_reg2, axis=[4, 8.5, 1.5, 4.5]) plt.scatter(X[y==0, 0], X[y==0, 1]) plt.scatter(X[y==1, 0], X[y==1, 1]) plt.scatter(X[y==2, 0], X[y==2, 1]) plt.show()
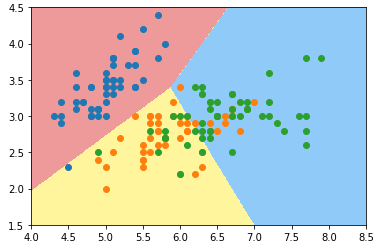
3)使用所有分类数据
- OvR
X = iris.data y = iris.target X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666) log_reg_ovr = LogisticRegression() log_reg_ovr.fit(X_train, y_train) log_reg_ovr.score(X_test, y_test) # 准确率:0.9473684210526315
- OvO
log_reg_ovo = LogisticRegression(multi_class='multinomial', solver='newton-cg') log_reg_ovo.fit(X_train, y_train) log_reg_ovo.score(X_test, y_test) # 准确率:1.0
4)分析
- 通过准确率对比可以看出,使用 OvO 方法改造 LogisticRegression() 算法,得到的模型准确率较高;
四、OvR 和 OvO 的封装
- scikit-learn单独封装了实现 OvO 和 OvR 的类,使得任意二分类算法都可以通过使用这两个类解决多分类问题;
1)OvR 的封装
- 模块
from sklearn.multiclass import OneVsRestClassifier
- 使用方法
- ovr = OneVsRestClassifier(二分类算法的实例对象):得到一个可以解决多分类的实例对象;
- ovr.fit(X_train, y_train):拟合多分类实例对象;
- 例
from sklearn.multiclass import OneVsRestClassifier ovr = OneVsRestClassifier(log_reg) ovr.fit(X_train, y_train) ovr.score(X_test, y_test) # 准确率:0.9473684210526315
2)OvO 的封装
- 模块
from sklearn.multiclass import OneVsOneClassifier
- 使用方法:同理 OvR;
- 例
from sklearn.multiclass import OneVsOneClassifier ovo = OneVsOneClassifier(log_reg) ovo.fit(X_train, y_train) ovo.score(X_test, y_test) # 准确率:1.0