据说这是面试算法岗位中最常问的问题,各个面经里面出现这个问题的比率很高,今天的算法课讲了《算法导论》的第九章“中位数和顺序统计量”,9.2和9.3恰恰介绍的就是这个问题,这里做一下总结,说一下自己的理解。
首先,接手这个问题最直接的想法莫过于排序了,常用的排序算法里面有冒泡排序、选择排序、插入排序、归并排序、堆排序、快速排序、计数排序、基数排序、桶排序等,虽然说快排的平均时间复杂度达到了O(nlgn),桶排序的平均时间复杂度达到了O(n)但是基于排序的方法对于这个问题并不是一个好的解决方法。O(nlgn)的排序就不说了,O(n)的排序前面隐含的常数因子也会被下面介绍的算法所打败。
接下来会想到的方法,可能是对整个数组过i遍,每次都选择最小的,这样第i次就选到了第i小的,这样的话时间复杂度就成了O(in),当i比较大时,仍然是不可接受的,万一i接近n/2呢,岂不是都O(n2)了。
期望线性时间复杂度算法
思考一下快排的PARTITION过程,经过多次左右互换,实现了针对于选定靶点A[q],左侧的元素都小于A[q],右侧的元素都大于A[q]。这个过程岂不是能用来帮助选点。
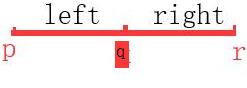
1 RANDOMIZED-SELECT(A,p,r,i) 2 if p==r 3 return A[p] 4 q = RANDOMIZED-PARTITION(A,p,r) //划分位置 5 k = q-p+1 6 if i==k //the pivot value is the answer 7 return A[q] 8 else if i<k 9 return RANDOMIZED-SELECT(A,p,q-1,i) 10 else return RANDOMIZED-SELECT(A,q+1,r,i-k)
第4行的划分位置是随机取到的,这样就为下面分析其期望时间复杂度埋下伏笔。k是left部分的长度。当i=k时,6、7行是k刚好满足长度要求,程序结束。第9行,意思是i<k时,程序进入left部分(注意递归处理的数组的范围的变化为A[p]~A[q-1]);当i>k时,进入right部分(注意递归处理的数组的范围的变化为A[q+1]~A[r],寻找的数的“位置”也要减去left部分的长度)。如此递归下去,则总会退出,即找到对应的第i小的数。
下面分析其时间复杂度。
最坏情况:假如第4行的RANDOMIZED-PARTITION(A,p,r) 每次划分的比例都是0:n-1(即最差情况),这样的话时间复杂度就是O(n2)。
平均情况:T(n)≤Σk=1nXk•(T(max(k-1,n-k))+O(n) ) = Σk=1nXk•T(max(k-1,n-k)) + O(n)
经过替换推导 E(T(n)) ≤ cn。即期望时间复杂度为线性时间复杂度。
最坏情况为线性时间点的选择算法
该算法比“期望线性时间复杂度算法”的主要改进是通过寻找中位数来得到一个更好的划分(上面的是随机取的划分位置)。SELECT算法使用的也是快速排序的确定性划分算法PARTITION,但做了修改,把划分的主元也作为输入参数。
通过执行下列步骤,算法SELECT可以确定一个有n>1个不同的元素的输入数组中第i小的元素。(如果n=1,则SEKECT只返回它的唯一输入数值作为第i小的元素 ) (1)将输入数组的n个元素划分为(n/5)组,每组5个元素,且至多只有一组由剩下的n mod 5个元素组成。 (2)寻找这(n/5)组中每一组中位数:首先对每组元素进行插入排序,然后确定每组有序元素的中位数。 (3)对第2步中找出的(n/5)个中位数,递归调用SELECT以找出其中位数x(如果有偶数个中位数,为了方便,约定x是较小的中位数) (4)利用修改过的PARTITION版本,按中位数的中位数x对输入数组进行划分。令k=划分的低区中的元素个数+1,因此x是第k小的元素,并且有n-k个元素在划分的高区。 (5)如果i=k,则返回x。如果i<k,则在低区递归调用SELECT来找出第i小的元素。如果i>k,则高区递归查找第i-k小的元素。
步骤1、2和4需要O(n)的时间。(步骤2是对大小为O(1)的集合调用O(n)次插入排序) 步骤3所需时间为T(n/5),步骤5所需时间至多为T(7n/10+6)(具体推导请参考算导9.3)。这样根据主方法就很容易推导出时间复杂度为线性。(T(n)≤cn)