算法导论读书笔记(2)
分治法
算法设计的方法有很多。插入排序 使用的是 增量 (incremental)方法:在排好子数组 A [ 1 .. j - 1 ]后,将元素 A [ j ]插入,形成排好序的子数组 A [ 1 .. j ]。
此外,有很多算法在结构上是 递归 的:为了解决一个给定的问题,算法要一次或多次地递归调用其自身来解决相关子问题。这些算法采用的是 分治策略 (divide-and-conquer):将原问题划分成 n 个规模较小而结构与原问题相似的子问题;递归地解决这些子问题,然后再合并其结果,就得到原问题的解。
分治模式在每一层递归上都有三个步骤:
- 分解(Divide):
- 将原问题分解成一系列子问题;
- 解决(Conquer)
- 递归地解各个子问题。若子问题足够小,则直接求解;
- 合并(Combine)
- 将子问题的结果合并成原问题的解。
归并排序
归并排序(merge sort)完全依照了上述模式,直观的操作如下:
- 分解:
- 将 n 个元素分成各含 n / 2个元素的子序列;
- 解决:
- 用归并排序法对两个子序列递归地排序;
- 合并:
- 合并两个已排序的子序列以得到排序结果。
对子序列排序时,其长度为1时递归结束。单个元素被视为是已排好序的。
归并排序的关键步骤在于合并两个已排序的子序列。这里引入一个辅助过程 MERGE(A, p, q, r) ,其中 A 为数组, p , q 和 r 都是下标,有 p <= q < r 。该过程假设子数组 A [ p .. q ]和 A [ q + 1 .. r ]都已排好序,并将它们合并成一个已排好序的子数组代替当前子数组 A [ p .. r ]。
MERGE(A, p, q, r) 1 n1 = q - p + 1 2 n2 = r - q 3 let L[1 .. n1 + 1] and R[1 .. n2 + 1] be new arrays 4 for i = 1 to n1 5 L[i] = A[p + i - 1] 6 for j = 1 to n2 7 R[j] = A[q + j] 8 L[n1 + 1] = MAX 9 R[n2 + 1] = MAX 10 i = 1 11 j = 1 12 for k = p to r 13 if L[i] <= R[j] 14 A[k] = L[i] 15 i = i + 1 16 else 17 A[k] = R[j] 18 j = j + 1
MERGE 过程的时间代价为 Θ ( n ),其中 n = r - p + 1。
现在,就可以讲 MERGE 过程作为归并排序中的一个子程序来使用了。下面的过程 MERGE-SORT(A, p, r) 对子数组 A [ p .. r ]排序。如果 p >= r ,则该子数组中至多只有一个元素,视为已排序。否则,分解步骤就计算出一个下标 q ,将 A [ p .. r ]分成 A [ p .. q ]和 A [ q + 1 .. r ],各含 FLOOR(n / 2) 1 个元素。
MERGE-SORT(A, p, r) 1 if p < r 2 q = (p + r) / 2 3 MERGE-SORT(A, p, q) 4 MERGE-SORT(A, q + 1, r) 5 MERGE(A, p, q, r)
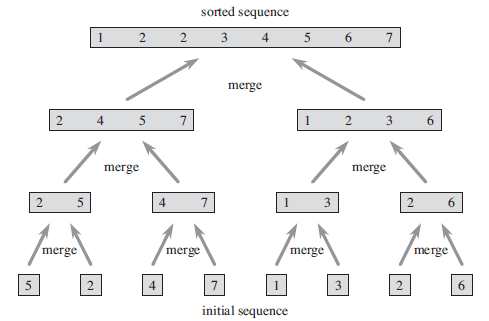
下图自底向上地展示了当 n 为2的幂时,整个过程中的操作。算法将两个长度为1的序列合并成已排序的,长度为2的序列,接着又将长度为2的序列合并成长度为4的序列,直到最终形成排好序的 n 的序列。
归并排序的简单Java实现:
/** * 归并排序 * * @param array */ public static void mergeSort(int[] array) { mergeSort(array, 0, array.length - 1); } private static void mergeSort(int[] array, int p, int r) { int q; if (p < r) { q = (p + r) >> 1; mergeSort(array, p, q); mergeSort(array, q + 1, r); merge(array, p, q, r); } } private static void merge(int[] array, int p, int q, int r) { int lLen = q - p + 1; int rLen = r - q; int[] left = new int[lLen + 1]; int[] right = new int[rLen + 1]; int i, j; for (i = 0; i < lLen; i++) left[i] = array[p + i]; for (j = 0; j < rLen; j++) right[j] = array[q + j + 1]; left[i] = Integer.MAX_VALUE; right[j] = Integer.MAX_VALUE; i = j = 0; for (int k = p; k <= r; k++) { if (left[i] <= right[j]) array[k] = left[i++]; else array[k] = right[j++]; } }
分治法分析
当一个算法中含有对其自身的递归调用时,其运行时间可以用一个 递归方程 (或 递归式 )来表示。该方程通过描述子问题与原问题的关系,来给出总的运行时间。
设 T ( n )为一个规模为 n 的问题的运行时间。如果问题的规模足够小,如 n <= c ( c 为一个常量),则得到它的直接解的时间为常量,写作 Θ (1)。假设我们把原问题分解成 a 个子问题,每一个的大小是原来的1 / b 。如果分解该问题和合并解的时间各为 D ( n )和 C ( n ),则得到递归式:
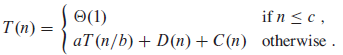
归并排序算法的分析
为简化分析,假定原问题的规模是2的幂,这样每次分解产生的子序列长度就恰好为 n / 2。
以下给出了归并排序 n 个数的运行时间。归并排序一个元素的时间是常量。当 n > 1时,将运行时间分解如下:
- 分解:
- 计算出子数组的中间位置,需要常量时间,因而 D ( n ) = Θ (1)。
- 解决:
- 递归地解两个规模为 n / 2的子问题,时间为2 T ( n / 2)。
- 合并:
MERGE过程的运行时间为 Θ ( n ),则 C ( n ) = Θ ( n )。
如此得到归并排序最坏情况下运行时间 T ( n )的递归表示:

递归式1
此处可以直观地看出 T ( n ) = Θ ( n lg n),重写递归式如下:
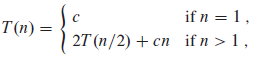
递归式2
其中常量 c 代表规模为1的问题所需的时间。
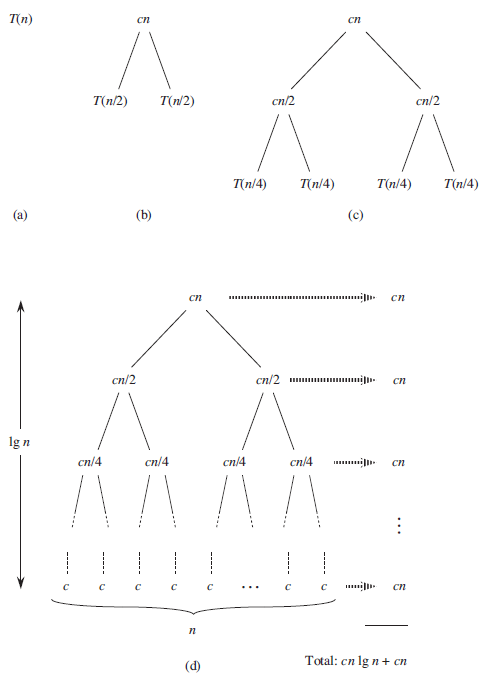
下图说明了如何解递归式2。它将 T ( n )扩展一种等价树形式。 c n 是树根(即顶层递归的代价),根的两棵子树是两个更小一点的递归式 T ( n / 2),它们的代价都是 c n / 2.继续扩展直到问题的规模降到了1,此时每个问题的代价为 c 。
接下来将树的每一层代价相加。一般来说,最顶层之下的第 i 层有 2i 个结点,每个的代价都是 c ( n / 2i ),于是,第 i 层的总代价为 2i c ( n / 2i )。
要计算递归式的总代价,只要将递归树中各层的代价加起来就可以。在该树中,共有lg n + 1层,每一层的代价都是 c n ,于是,树的总代价为 c n (lg n + 1) = c n lg n + c n 。忽略低阶项和常量,得到结果 Θ ( n lg n )。
练习
2.3-2
改写 MERGE 过程,不使用哨兵元素。
MERGE(A, p, q, r) 1 n1 = q - p + 1; 2 n2 = r - q; 3 let L[1 .. n1] and R[1 .. n2] be new arrays 4 for i = 1 to n1 5 L[i] = A[p + i - 1] 6 for j = 1 to n2 7 R[j] = A[q + j] 8 i = j = 1 9 k = p 10 while i <= n1 and j <= n2 11 if L[i] <= R[j] 12 A[k] = L[i] 13 k = k + 1 14 i = i + 1 15 else 16 A[k] = R[j] 17 j = j + 1 18 while i <= n1 19 A[k] = L[i] 20 k = k + 1 21 i = i + 1 22 while j <= n2 23 A[k] = R[j] 24 j = j + 1
2.3-4
将插入排序改写成递归过程,并写出运行时间的递归式。
INSERTION-SORT-RECURSIVE(A, p) 1 if p > 1 2 key = A[p] 3 p = p - 1 4 INSERTION-SORT-RECURSIVE(A, p) 5 INSERTION-ELEMENT(A, p, key)
INSERTION-ELEMENT(A, p, key) 1 while p > 0 and A[p] > key 2 A[p + 1] = A[p] 3 p = p - 1 4 A[p + 1] = key
该过程的运行时间如下分解:
- 分解:
- 缩小子数组规模,需要常量时间 D ( n ) = Θ (1)。
- 解决:
- 递归地解一个规模为 n - 1的子问题,时间为 T ( n - 1)。
- 合并:
INSERTION-ELEMENT过程的运行时间是线性的,即 C ( n ) = Θ ( n )。
则递归版本插入排序的递归式可写为 T ( n ) = T ( n - 1) + Θ ( n )。最终结果就是 T ( n ) = Θ ( n2 )。
2.3-5
二分查找伪码:
BINARY-SEARCH(A, v) 1 front = 1 2 end = A.length 3 while front < end 4 middle = (front + end) / 2 5 if A[middle] < v 6 front = middle + 1 7 else if A[middle] > v 8 end = middle - 1 9 else 10 return middle 11 return -1
2.3-7
设计算法:查找集合 S 中是否存在两个其和等于 x 的元素。
CHECK-SUM(S, x) 1 A = MERGE-SORT(S) 2 for i = 1 to A.length 3 v = x - A[i] 4 if BINARY-SEARCH(A, v) > 0 5 return true 6 return false
思考题
在归并排序中对小数组采用插入排序
尽管归并排序的最坏情况运行时间为 Θ ( n lg n ),插入排序的最坏情况运行时间为 Θ ( n2 ),但插入排序中的常数因子使得它在 n 比较小时,运行得要更快一些。因此,在归并排序算法中,当子问题足够小的时候,采用插入排序就比较合适了。考虑对归并排序作这样的修改,即采用插入排序策略,对 n / k 个长度为 k 的子列表进行排序,然后,再用标准的合并机制将它们合并起来,此处 k 是一个待定值。
假设 n / k 是2的幂(这样可以很容易的算出树的高度),设 T ( n )为该算法最坏情况运行时间,则函数的等价树结构如下:

可以看到,树共有lg( n / k ) + 1层,最底层共有 n / k 个结点,每个结点都是长度为 k 的子列表。规模为 k 的插入排序的最坏情况运行时间是关于 k 的二次函数,表示为 T ( k ) = a k2 + b k + c 。共有 n / k 个这样的子序列,所以总的运行时间 L ( n ) = ( n / k ) T ( k )。最终可知, n / k 个子列表(每个子列表的长度为 k )可以用插入排序在 Θ ( n k )时间内完成排序。
可知树共有lg( n / k ) + 1层。除最后一层外,其余各层全部用于合并子列表,每一层的代价都是 c n 。最后一层的时间代价已知为 Θ ( n k )。所以算法总的运行时间就是 T ( n ) = c n lg( n / k ) + Θ ( n k )。舍弃低阶项和常数因子,有 T ( n ) = Θ ( n lg( n / k ))。
逆序对
设 A [ 1 .. n ]是一个包含 n 个不同数的数组。如果在 i < j 的情况下,有 A [ i ] > A [ j ],则( i , j )就称为 A 中的一个 逆序对 (inversion)。
降幂排列的数组拥有的逆序对是最多的,对于长度为 n 的数组来说,共有( n - 1)!个逆序对。
脚注
FLOOR(x) 记号表示小于等于 x 的最大整数, CEIL(x) 表示大于等于 x 的最小整数。