| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 9757 | Accepted: 3004 |
Description
The repetition number of a string is defined as the maximum number R such that the string can be partitioned into R same consecutive substrings. For example, the repetition number of "ababab" is 3 and "ababa" is 1.
Given a string containing lowercase letters, you are to find a substring of it with maximum repetition number.
Input
The input consists of multiple test cases. Each test case contains exactly one line, which
gives a non-empty string consisting of lowercase letters. The length of the string will not be greater than 100,000.
The last test case is followed by a line containing a '#'.
Output
For each test case, print a line containing the test case number( beginning with 1) followed by the substring of maximum repetition number. If there are multiple substrings of maximum repetition number, print the lexicographically smallest one.
Sample Input
ccabababc daabbccaa #
Sample Output
Case 1: ababab Case 2: aa
Source
【题意】:
给定一个串,长度<=10^5,求它重复次数最多的连续重复子串(输出字典序最小的那个)。
例如ccabcabc,答案就是abcabc

原理:
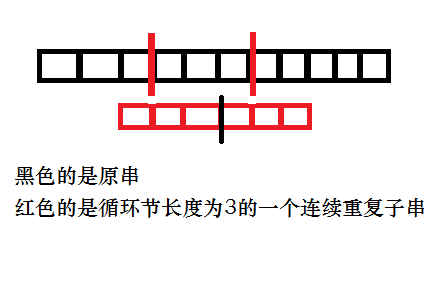
按照L划分,因为相邻两个i之间隔着一个L,s[i*L]和s[(i+1)*L]必定是真正循环节的同一个位置。
对于当前的L,i,i+1,x=s[i*L],y=s[(i+1)*L],找前找后,知道了最早能匹配到t0,最晚能匹配到t1,因为不知道当前的起始点是真正循环节的第几个点,所以我们要往前找L个点看看它们是不是真正的起始点。
(转载自KonjakJuruo)
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; const int N=1e5+10; int n,cas,c[N],h[N],sa[N],tsa[N],rank[N],trank[N]; int log2[N],f[N][20]; char s[N]; void DA(int maxx=30){ int p; for(int i=0;i<=maxx;i++) c[i]=0; for(int i=1;i<=n;i++) c[rank[i]=s[i]-'a'+1]++; for(int i=2;i<=maxx;i++) c[i]+=c[i-1]; for(int i=n;i;i--) sa[c[rank[i]]--]=i; trank[sa[1]]=p=1; for(int i=2;i<=n;i++){ if(rank[sa[i]]!=rank[sa[i-1]]) p++; trank[sa[i]]=p; } for(int i=1;i<=n;i++) rank[i]=trank[i]; for(int k=1;p<n;k<<=1,maxx=p){ p=0; for(int i=n-k+1;i<=n;i++) tsa[++p]=i; for(int i=1;i<=n;i++) if(sa[i]>k) tsa[++p]=sa[i]-k; for(int i=0;i<=maxx;i++) c[i]=0; for(int i=1;i<=n;i++) trank[i]=rank[tsa[i]]; for(int i=1;i<=n;i++) c[trank[i]]++; for(int i=2;i<=maxx;i++) c[i]+=c[i-1]; for(int i=n;i;i--) sa[c[trank[i]]--]=tsa[i]; trank[sa[1]]=p=1; for(int i=2;i<=n;i++){ if(rank[sa[i]]!=rank[sa[i-1]]||rank[sa[i]+k]!=rank[sa[i-1]+k]) p++; trank[sa[i]]=p; } for(int i=1;i<=n;i++) rank[i]=trank[i]; } for(int i=1,k=0;i<=n;i++){ int j=sa[rank[i]-1]; while(s[i+k]==s[j+k]) k++; h[rank[i]]=k;if(k>0) k--; } } void RMQ(){ for(int i=1;i<=n;i++) f[i][0]=h[i]; for(int i=2;i<=n;i++) log2[i]=log2[i>>1]+1; for(int j=1;j<=log2[n];j++){ for(int i=1;i+(1<<j)-1<=n;i++){ f[i][j]=min(f[i][j-1],f[i+(1<<j-1)][j-1]); } } } int query(int l,int r){ int a=rank[l],b=rank[r]; if(a>b) swap(a,b); a++; int k=log2[b-a+1]; return min(f[a][k],f[b-(1<<k)+1][k]); } int main(){ while(scanf("%s",s+1)==1){ n=strlen(s+1); if(n==1&&s[1]=='#') break; printf("Case %d: ",++cas); DA();RMQ(); int t0=0,t1=0,al=0,ar=0,ans=0; int lim=n>>1; for(int L=1,x,y,z;L<=lim;L++){ for(int i=0;L*(i+1)+1<=n;i++){ x=L*i+1;y=L*(i+1)+1; if(s[x]!=s[y]) continue; z=query(x,y); t1=y+z-1;//直接找右端点 t0=0; for(int j=0;j<L;j++){//往左匹配,找左端点 if(x-j<1||s[x-j]!=s[y-j]) break; t0=x-j; int now=(t1-t0+1)/L; if(ans<now||(ans==now&&rank[t0]<rank[al])){ ans=now; al=t0; ar=t0+now*L-1; } } } } if(!ans) printf("%c ",s[sa[1]]); else{ s[ar+1]=0; puts(s+al); } } return 0; }