Anderson《空气动力学基础》5th读书笔记第5记——推导二维机翼的空气动力学系数

Anderson《空气动力学基础》5th读书笔记第5记——推导二维机翼的空气动力学系数

机翼的受力分析图

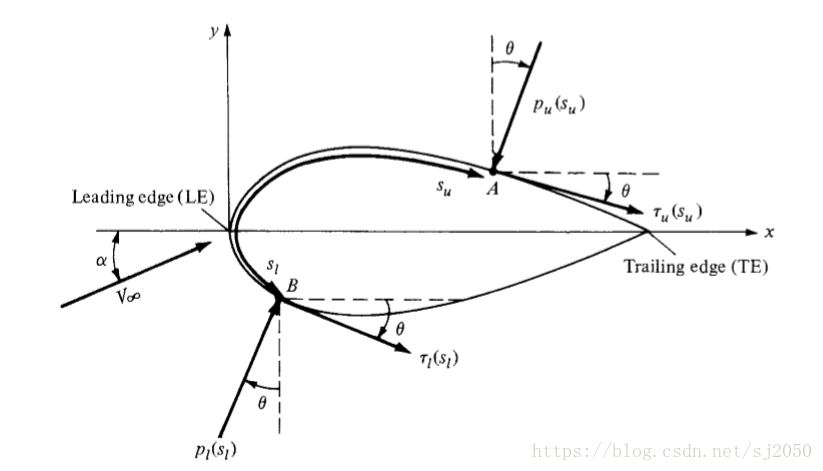
我们知道，空气对一个物体产生的升力和阻力以及力矩源于作用在整个物体上的压力分布和剪切力分布，所以我们分析上图可知（取单位展长的机翼）：

对于上表面：
$dN_{u}^{'} = -p_{u}ds_{u}cos heta - au _{u}ds_{u}sin heta$

$dA_{u}^{'} = -p_{u}ds_{u}cos heta + au _{u}ds_{u}sin heta$

同理对于下表面：

$dN_{l}^{'} = p_{l}ds_{l}cos heta - au _{l}ds_{l}sin heta$

$dA_{l}^{'} = p_{l}ds_{l}cos heta + au _{l}ds_{l}sin heta$

PS：N为法向力，A为切向力。

于是单位机翼上的总的法向力和切向力可表示为：

   $N^{'} = -int_{LE}^{TE}(p_{u}cos heta + au _{u}sin heta )ds_{u}+int_{LE}^{TE}(p_{l}cos heta - au _{l}sin heta )ds_{l}$

$A^{'} = int_{LE}^{TE}(-p_{u}sin heta + au _{u}cos heta )ds_{u}+int_{LE}^{TE}(p_{l}sin heta + au _{l}cos heta )ds_{l}$ (LE代表前缘，TE代表后缘)

我们再推导机翼受到的力矩：

上表面受到的微元力矩：

$dM_{u}^{'} = (p_{u}cos heta + au _{u}sin heta )xds_{u}+(-p_{u}sin heta + au _{u}cos heta )yds_{u}$

$dM_{l}^{'} = (-p_{l}cos heta + au _{l}sin heta )xds_{l}+(p_{l}sin heta + au _{l}cos heta )yds_{l}$

我们需要对力矩的方向做一些解释，我们规定力矩方向如下图所示：

因此我们可以知道机翼的总力矩为：

$M_{LE}^{'} = int_{LE}^{TE} [(p_{u}cos heta + au _{u}sin heta )x+(-p_{u}sin heta + au _{u}cos heta )y]ds_{u}+int_{LE}^{TE}[ (-p_{l}cos heta + au _{l}sin heta )x+(p_{l}sin heta + au _{l}cos heta )y]ds_{l}$

我们又知道空气动力学系数为：

$c_{n} equiv frac{N^{'}}{q_{infty}c}$     $c_{a} equiv frac{A^{'}}{q_{infty}c}$     $c_{m} equiv frac{M^{'}}{q_{infty}c^{2}}$ $c_{p} equiv frac{P^{'}}{q_{infty}}$    PS:其中 $q_{infty } equiv frac{1}{2} ho _{infty }V_{infty }^{2}$

不知道上面这些无量纲系数是怎么来的，别怕，请参考：量纲分析——白金汉PI定理

二维机翼的几何关系

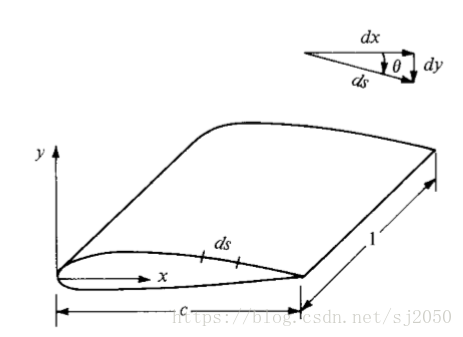
从上图中，我们又可以很轻松地推导出：

$dx = ds cos heta$    $dy = -(ds sin heta )$    $S = c(1)$

有了以上这些公式我们就可以来推导 $c_{n}$    $c_{a}$ $c_{m_{LE}}$     $c_{l}$    $c_{d}$

由于他们三者推导过程类似，所以我们只对 $c_{n}$ 做详细推导：

1.已知 $N^{'} = -int_{LE}^{TE}(p_{u}cos heta + au _{u}sin heta )ds_{u}+int_{LE}^{TE}(p_{l}cos heta - au _{l}sin heta )ds_{l}$ 以及 $c_{n} equiv frac{N^{'}}{q_{infty}c}$ 、

$dx = ds cos heta$ 、 $dy = -(ds sin heta )$ 、 $S = c(1)$ 、 $c_{p} equiv frac{P^{'}}{q_{infty}}$

2. 对 $c_{n} equiv frac{N^{'}}{q_{infty}c}$ 进行代换得到： $c_{n} = frac{-int_{0}^{c}(p_{u} cos heta + au _{u }sin heta)/cos heta dx+int_{0}^{c}(p_{l} cos heta - au _{l}sin heta)/cos heta dx}{q_{infty }c}$

3. 进行化简： $c_{n} = frac{-int_{0}^{c}(C_{p_{u}} + C_{f _{u }}sin heta/cos heta) dx+int_{0}^{c}(C_{p_{l}} - C_{f _{l }}sin heta/cos heta) dx}{c}$

4.又因为易推    $frac{sin heta }{cos heta} = -frac{dy}{dx}$

5.带入3中式子，最终可得：

    $c_{n} = frac{int_{0}^{c}(-C_{p_{u}} +C_{p_{l}}) dx+int_{0}^{c}( C_{f _{u }}frac{dy_{u}}{dx} + C_{f _{l }}frac{dy_{l}}{dx}) dx}{c}$

同理，我们可以可以推的：

   $c_{a} = frac{int_{0}^{c}( C_{p _{u }}frac{dy_{u}}{dx} - C_{p_{l }}frac{dy_{l}}{dx}) dx+int_{0}^{c}(C_{f_{u}} +C_{f_{l}}) dx}{c}$

   $c_{m_{LE}} = frac{int_{0}^{c}(C_{p_{u}} -C_{p_{l}})x dx-int_{0}^{c}( C_{f _{u }}frac{dy_{u}}{dx} + C_{f _{l }}frac{dy_{l}}{dx}) dx+int_{0}^{c}( C_{p _{u }}frac{dy_{u}}{dx} + C_{f_{u}}) y_{u}dx+int_{0}^{c}( -C_{p_{l }}frac{dy_{l}}{dx}+C_{f_{l}} ) dx}{c^{2}}$

   $c_{l} = c_{n}cosalpha - c_{a}sinalpha$

   $c_{d} = c_{n}sinalpha + c_{a}cosalpha$

至此，二维机翼的空气动力学系数基本都推导完毕了，有人问干嘛把公式推这么复杂，其实答案很简单，就如我们一开始所说的空气对一个物体产生的升力和阻力以及力矩源于作用在整个物体上的压力分布和剪切力分布，记住压力分布和剪切力分布是祖先，其他所有的力都是这两个力衍生下去的，这也就是为什么我们推导公式时要把其他空气动力学系数尽量用压力和剪切力系数来表示，有根才有枝嘛！
相关阅读:
Valid Parentheses [LeetCode 20]
线性回归的Spark实现 [Linear Regression / Machine Learning / Spark]
逻辑回归的分布式实现 [Logistic Regression / Machine Learning / Spark ]
Python爬虫之豆瓣-新书速递-图书解析
 安装软件包
 打包与压缩
 linux与linux间，互相拷贝文件
 网络管理
 重定向和管道
 索引
原文地址：https://www.cnblogs.com/sj2050/p/13413710.html

Anderson《空气动力学基础》5th读书笔记 第5记——推导二维机翼的空气动力学系数

Anderson《空气动力学基础》5th读书笔记第5记——推导二维机翼的空气动力学系数