二叉搜索树
二叉搜索树很明显来自于一种思想:二分查找。
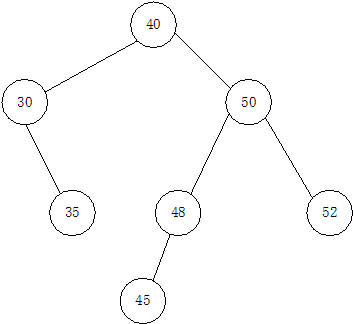
二叉搜索树
很明显:
- 二叉搜索树并不要求是一棵完全二叉树
- 则左子树上所有结点的值均小于它的根结点的值;右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉搜索树。
对于二叉搜索树而言,有以下典型的操作:
1 插入,删除
2 查找
3 遍历:深度优先遍历(包括前序,中序,后序三种方式),广度优先遍历
对于插入而言:是一个比较简单的过程。自己思考代码的实现。
删除操作比较麻烦,先不讲
而关于查找操作吗,和插入操作差别不大,不讲
关于三种深度优先遍历:其中中序遍历可以将节点按顺序输出,后序遍历可以用来销毁二叉树(销毁二叉树,需要先删除左子节点,然后删除右子节点,然后才是根节点。
重点说一下广度优先遍历:
对于图示二叉搜索树,明显广度优先遍历的结果是:40,30,50,35,48,52,45.那么在计算中该如何实现这个东西呢?
其核心思想在于:队列的使用,如下图
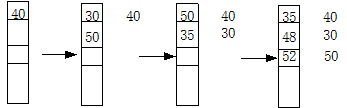
将根节点40入队,将40出队,如果其有左右子节点,将左右子节点依次入队,再将(左右)子节点出队,在出队的时候,检查该左右子节点是否还有孩子节点,如果有,继续将孩子节点入队。
核心在于,每做完一次的出队操作,都要检查当前出队节点是否存在孩子节点,如果有,将孩子节点入队。直到队列为空!
下面讲解在二叉排序树中的删除问题:
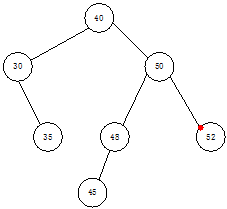
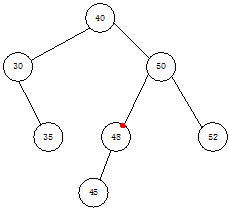

上述三张图给出了二叉排序树节点删除的3种情况:
- 删除的节点是叶子节点
- 删除的节点只有一个孩子节点(左孩子或右孩子)
- 删除的节点有左右孩子(子树)
针对情况1:直接将节点删除即可
针对情况2:用删除节点的孩子节点代替删除节点
针对情况3:我们需要考虑其前驱或者后继节点(前驱节点是key值上比该节点小的前一个节点,后继是key值比该节点大的后一个节点)。我们用该节点的前驱节点或者后继节点替代该节点:例如上图中我们用key值为45的节点或key值为52的节点替代key值为50的节点。
关于二叉搜索树的总结和思考:
二叉搜索树的定义已经说明了,它存在的意义就是为了更快速的查找。使得我们线性表下的 的查找效率,降低为
的查找效率,降低为 。但同时我们应该明白:由于二叉排序树只是宽泛的说明了节点键值的关系,对于树的结构并没有严格的限制,那么这样的树也可能是非平衡的。这将会导致查找效率的降低,极端的条件下直接退化为链表。为此,才会有类似于平衡树这些概念。
。但同时我们应该明白:由于二叉排序树只是宽泛的说明了节点键值的关系,对于树的结构并没有严格的限制,那么这样的树也可能是非平衡的。这将会导致查找效率的降低,极端的条件下直接退化为链表。为此,才会有类似于平衡树这些概念。