题目如下:
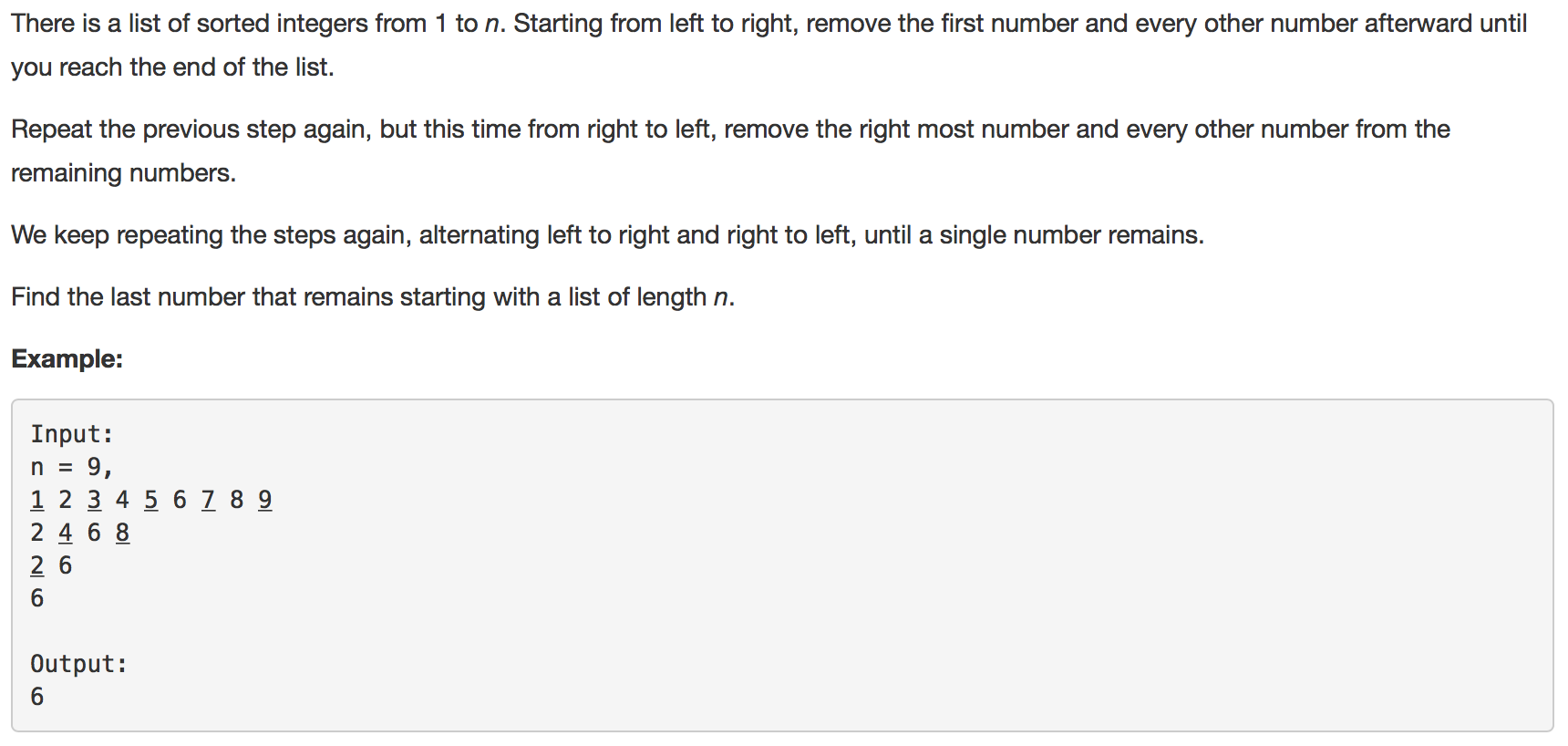
解题思路:对于这种数字类型的题目,数字一般都会有内在的规律。不管怎么操作了多少次,本题的数组一直是一个等差数列。从[1 2 3 4 5 6 7 8 9] -> [2 4 6 8] -> [2 6] -> [6]这个序列中,我们可以得到公差分别是1,2,4。如果我们把n扩大一点,打印出其中每一步剩余的数组序列,我们很容易发现公差是pow(2,n)次方,发现了这个规律后,一切就水到渠成了。接下来,我们只要记录每一次操作后剩下序列的low,high以及序列的长度,直到最后序列只有一个元素即可。
代码如下:
class Solution(object): def lastRemaining(self, n): """ :type n: int :rtype: int """ if n == 1: return 1 times = 1 low = high = None length = n multiple = None while True: if times == 1: length = length / 2 low = 2 if n % 2 == 0: high = n else: high = n -1 multiple = pow(2, times) elif times % 2 == 0: length = length / 2 high -= multiple multiple = pow(2, times) low = high - multiple*(length-1) else: length = length / 2 low += multiple multiple = pow(2, times) high = low + multiple * (length - 1) times += 1 if low >= high: return high