Einbahnstrasse
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3031 Accepted Submission(s):
940
Problem Description
Einbahnstra  e (German for a one-way street) is
a street on which vehicles should only move in one direction. One reason for
having one-way streets is to facilitate a smoother flow of traffic through
crowded areas. This is useful in city centers, especially old cities like Cairo
and Damascus. Careful planning guarantees that you can get to any location
starting from any point. Nevertheless, drivers must carefully plan their route
in order to avoid prolonging their trip due to one-way streets. Experienced
drivers know that there are multiple paths to travel between any two locations.
Not only that, there might be multiple roads between the same two locations.
Knowing the shortest way between any two locations is a must! This is even more
important when driving vehicles that are hard to maneuver (garbage trucks,
towing trucks, etc.)
e (German for a one-way street) is
a street on which vehicles should only move in one direction. One reason for
having one-way streets is to facilitate a smoother flow of traffic through
crowded areas. This is useful in city centers, especially old cities like Cairo
and Damascus. Careful planning guarantees that you can get to any location
starting from any point. Nevertheless, drivers must carefully plan their route
in order to avoid prolonging their trip due to one-way streets. Experienced
drivers know that there are multiple paths to travel between any two locations.
Not only that, there might be multiple roads between the same two locations.
Knowing the shortest way between any two locations is a must! This is even more
important when driving vehicles that are hard to maneuver (garbage trucks,
towing trucks, etc.)
You just started a new job at a car-towing company. The company has a number of towing trucks parked at the company's garage. A tow-truck lifts the front or back wheels of a broken car in order to pull it straight back to the company's garage. You receive calls from various parts of the city about broken cars that need to be towed. The cars have to be towed in the same order as you receive the calls. Your job is to advise the tow-truck drivers regarding the shortest way in order to collect all broken cars back in to the company's garage. At the end of the day, you have to report to the management the total distance traveled by the trucks.
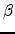 e (German for a one-way street) is
a street on which vehicles should only move in one direction. One reason for
having one-way streets is to facilitate a smoother flow of traffic through
crowded areas. This is useful in city centers, especially old cities like Cairo
and Damascus. Careful planning guarantees that you can get to any location
starting from any point. Nevertheless, drivers must carefully plan their route
in order to avoid prolonging their trip due to one-way streets. Experienced
drivers know that there are multiple paths to travel between any two locations.
Not only that, there might be multiple roads between the same two locations.
Knowing the shortest way between any two locations is a must! This is even more
important when driving vehicles that are hard to maneuver (garbage trucks,
towing trucks, etc.)
e (German for a one-way street) is
a street on which vehicles should only move in one direction. One reason for
having one-way streets is to facilitate a smoother flow of traffic through
crowded areas. This is useful in city centers, especially old cities like Cairo
and Damascus. Careful planning guarantees that you can get to any location
starting from any point. Nevertheless, drivers must carefully plan their route
in order to avoid prolonging their trip due to one-way streets. Experienced
drivers know that there are multiple paths to travel between any two locations.
Not only that, there might be multiple roads between the same two locations.
Knowing the shortest way between any two locations is a must! This is even more
important when driving vehicles that are hard to maneuver (garbage trucks,
towing trucks, etc.)You just started a new job at a car-towing company. The company has a number of towing trucks parked at the company's garage. A tow-truck lifts the front or back wheels of a broken car in order to pull it straight back to the company's garage. You receive calls from various parts of the city about broken cars that need to be towed. The cars have to be towed in the same order as you receive the calls. Your job is to advise the tow-truck drivers regarding the shortest way in order to collect all broken cars back in to the company's garage. At the end of the day, you have to report to the management the total distance traveled by the trucks.
Input
Your program will be tested on one or more test cases.
The first line of each test case specifies three numbers (N , C , and R )
separated by one or more spaces. The city has N locations with distinct names,
including the company's garage. C is the number of broken cars. R is the number
of roads in the city. Note that 0 < N < 100 , 0<=C < 1000 , and R
< 10000 . The second line is made of C + 1 words, the first being the
location of the company's garage, and the rest being the locations of the broken
cars. A location is a word made of 10 letters or less. Letter case is
significant. After the second line, there will be exactly R lines, each
describing a road. A road is described using one of these three
formats:
A -v -> B
A <-v - B
A <-v -> B
A and B are names of two different locations, while v is a positive integer (not exceeding 1000) denoting the length of the road. The first format specifies a one-way street from location A to B , the second specifies a one-way street from B to A , while the last specifies a two-way street between them. A , ``the arrow", and B are separated by one or more spaces. The end of the test cases is specified with a line having three zeros (for N , C , and R .)
The test case in the example below is the same as the one in the figure.
A -v -> B
A <-v - B
A <-v -> B
A and B are names of two different locations, while v is a positive integer (not exceeding 1000) denoting the length of the road. The first format specifies a one-way street from location A to B , the second specifies a one-way street from B to A , while the last specifies a two-way street between them. A , ``the arrow", and B are separated by one or more spaces. The end of the test cases is specified with a line having three zeros (for N , C , and R .)
The test case in the example below is the same as the one in the figure.

Output
For each test case, print the total distance traveled
using the following format:
k . V
Where k is test case number (starting at 1,) is a space, and V is the result.
k . V
Where k is test case number (starting at 1,) is a space, and V is the result.
Sample Input
4 2 5
NewTroy Midvale Metrodale
NewTroy <-20-> Midvale
Midvale --50-> Bakerline
NewTroy <-5-- Bakerline
Metrodale <-30-> NewTroy
Metrodale --5-> Bakerline
0 0 0
Sample Output
1. 80
Source
Recommend
简单的最短路,可以使用floyd或者两次dijst解决,不过因为题目的输入,导致处理数据有点麻烦。
题意:给出三个数 n, c, r
n 个地点(包括公司的车库),c 表示c辆车抛锚的地点, r 条道路
第二行给出 c+1 个地点,第一个为车库地点, 其余的 c 个为车的地点。
接下来的 r 行表示 r 条有向的道路,
s1 -- d -> s2 表示 s1到s2 的长度为 d
s1 <- d -- s2 表示 s2到s1 的长度为 d
s1 <- d -> s2 表示 s1到s2为双向边, 且长度为 d
拖车从车库出发到每个地点,在该地点拖回抛锚的车子。一辆拖车一次只能拖回一辆车子。注意:同一个地点可能有多辆抛锚的车子求总的路径长度。还要输出 case number
附上代码:
1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <map> 5 #define inf 0x3f3f3f3f 6 #define M 105 7 using namespace std; 8 int n,c,m,t; 9 int maps[M][M]; 10 char str[1005][M]; 11 map<string,int> mat; 12 13 void floyd() //小于100,使用floyd处理 14 { 15 int i,j,k; 16 for(k=1; k<=n; k++) 17 for(i=1; i<=n; i++) 18 for(j=1; j<=n; j++) 19 if(maps[i][j]>maps[i][k]+maps[k][j]) 20 maps[i][j]=maps[i][k]+maps[k][j]; 21 } 22 23 int main() 24 { 25 int i,j,s,x,y,start,Case=1; 26 char s1[M],s2[M]; 27 char from,to; 28 while(~scanf("%d%d%d",&n,&c,&m)) 29 { 30 if(!n&&!m&&!c) 31 break; 32 int sum=0; 33 mat.clear(); //map函数清空 34 for(i=0; i<=n; i++) 35 for(j=0; j<=n; j++) 36 if(i==j) maps[i][j]=0; 37 else maps[i][j]=inf; 38 for(i=0; i<=c; i++) 39 scanf("%s",str[i]); 40 t=1; 41 for(i=0; i<m; i++) 42 { 43 scanf("%s %c-%d-%c %s",s1,&from,&s,&to,s2); //注意这里的输入 44 if(!mat[s1]) mat[s1]=t++; //运用了map函数,假如s1不在mat中,则存入,并加1 45 if(!mat[s2]) mat[s2]=t++; 46 x=mat[s1],y=mat[s2]; 47 if(from=='<'&&s<maps[y][x]) 48 maps[y][x]=s; 49 if(to=='>'&&s<maps[x][y]) 50 maps[x][y]=s; 51 } 52 floyd(); 53 start=mat[str[0]]; //找寻起点在mat中存储的位置 54 for(i=1; i<=c; i++) 55 sum+=maps[start][mat[str[i]]]+maps[mat[str[i]]][start]; //注意去和回!! 56 printf("%d. %d ",Case++,sum); 57 } 58 return 0; 59 }