生存分析与R
生存分析是将事件的结果和出现这一结果所经历的时间结合起来分析的一类统计分析方法。不仅考虑事件是否出现,而且还考虑事件出现的时间长短,因此这类方法也被称为事件时间分析(time-to-event analysis)。生存分析是医学领域中一个重要的内容,在肿瘤等疾病的研究中运用十分广泛。
1.生存分析中的重要概念
生存分析的数据资料与其它一般的数据资料有一些不同的特征:
1. 其同时考虑生存时间和生存结局
2. 通常存在删失(censored)数据
3. 生存时间通常不服从生态分布。
1.1 生存时间
生存时间(survival time)指的是从开始事件到终点事件所经历的事件跨度。例如,急性白血病患者从发病到死亡所经历的事件跨度,冠心病患者两次发作之间的时间间隔等。
注意:在进行实验设计时,需要对起始事件、终点事件、时间单位进行明确的定义。
1.2 删失
生存结局(status)一般分为「死亡」和删失两类。「死亡」指的是我们感兴趣的终点事件(如白血病患者死亡、冠心病患者第二次发病)。除此之外的结局或生存结局则归类为删失(censoring),也称为截尾或终检。
删失的一般原因有:
1. 研究截至日期时,感兴趣终点事件仍未出现
2. 失访,不知道感兴趣终点事件何时发生或是否会发生
3. 因各种原因中途退出
4. 死于其它「事件」,如交通意外或其他疾病
2 生存分析的统计学方法与R的实现
生存分析拥有着与其它分析不同的统计学方法。
1. 描述统计:常采用Kaplan-Meier法进行分析,并绘制生存曲线;对于频数表资料,则可以采用寿命表进行分析(属于非参数统计方法)
2. 比较分析:我们经常需要对不同组别的生存率进行比较分析,比如比较使用或不用某种药物的HIV阳性患者的生存率是否不同。经常采用的log-rank检验以及Breslow检验。检验的零假设为:两组或多组总体生存时间分布相同。
3. 影响因素分析:我们可以建立生存模型来探讨哪些因素影响生存时间。常用的方法有两类,一类为半参数法:Cox比例风险模型;还有一类为参数法,主要有logistic分布法、Gompertz分布法等回归模型。
2.1 用R绘制生存曲线
在R中进行生存分析常用的包有survival包以及survminer包。
- survival 包提供了生存函数的建立,Cox模型的建立,以及比较分析。这个包也提供了基于基础绘图系统的生存曲线绘制。
- * survminer包*提供了基于ggplot2系统的可视化,具有更加美观的图形,以及定制方式。
2.1.1 数据集(data set)
我们在这里使用的数据集是survival包中含有的肺癌数据集:lung。前6条数据如下:
> library(survival)
## 前6条数据
> head(lung)
inst time status age sex ph.ecog ph.karno pat.karno meal.cal wt.loss
1 3 306 2 74 1 1 90 100 1175 NA
2 3 455 2 68 1 0 90 90 1225 15
3 3 1010 1 56 1 0 90 90 NA 15
4 5 210 2 57 1 1 90 60 1150 11
5 1 883 2 60 1 0 100 90 NA 0
6 12 1022 1 74 1 1 50 80 513 0- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
解释:
- inst: Institution code
- time: Survival time in days
- status: censoring status 1=censored, 2=dead
- age: Age in years
- sex: Male=1 Female=2
- ph.ecog: ECOG performance score (0=good 5=dead)
- ph.karno: Karnofsky performance score (bad=0-good=100) rated by physician Karnofsky
- pat.karno: performance score as rated by patient
- meal.cal: Calories consumed at meals
- wt.loss: Weight loss in last six months
2.1.2 生存曲线的拟合
survival包中的Sruv 函数可以创建一个生存对象。
>fit.surv <-Surv(lung$time,lung$status)
> head(fit.surv)
[1] 306 455 1010+ 210 883 1022+- 1
- 2
- 3
该函数根据是否为删失,将时间进行分类。右侧带有「+」号,代表为删失数据。
这时,我们可以使用survival包中的survfit函数用Kaplan-Meier法进行生存曲线的拟合。
> km<-survfit(fit.surv~1,data = lung)- 1
同时,我们也可以将其根据年龄(age)分为两组进行拟合:
>km_2<- survfit(fit.surv~sex,data=lung)- 1
2.1.3 生存曲线可视化的方法:
可视化方法有两种,一种是基于基础绘图系统的plot,还有一种是基于ggplot2绘图系统的ggsurvplot。
我们可以使用基于基础绘图系统的plot函数将其可视化:
plot (km)- 1
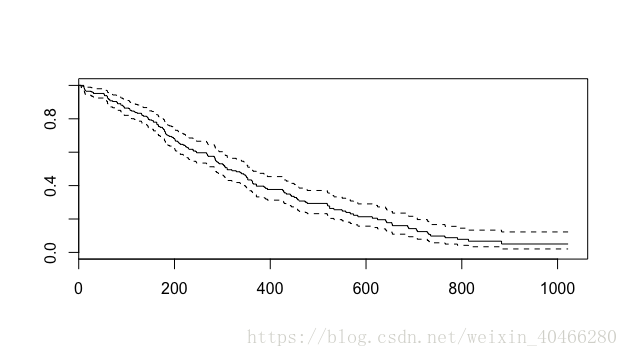
分组的生存曲线:
plot (km_2)- 1
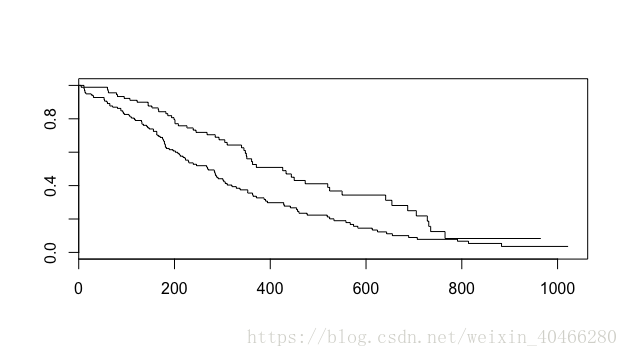
这种基于基础绘图系统的可视化方法较为简陋,可以修改的也参数也较少。目前在R语言中,可视化功能极其强大的是ggplot2系统。survminer包提供了基于ggplot2系统的可视化函数:ggsurvplot
library(survminer)
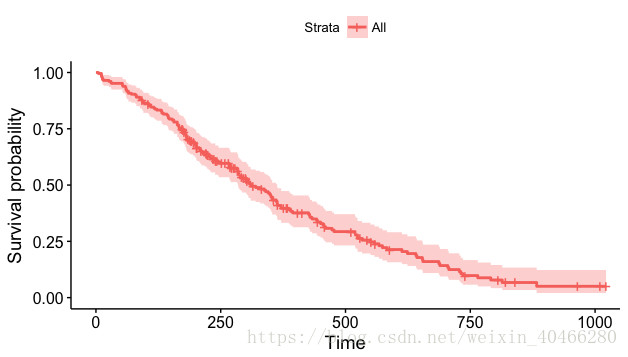
ggsurvplot (km)- 1
- 2
ggsurvplot (km_2)- 1
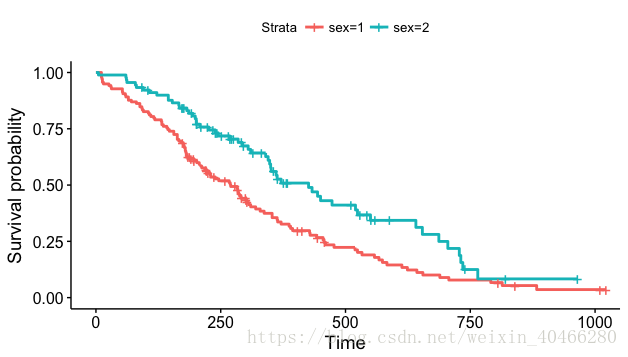
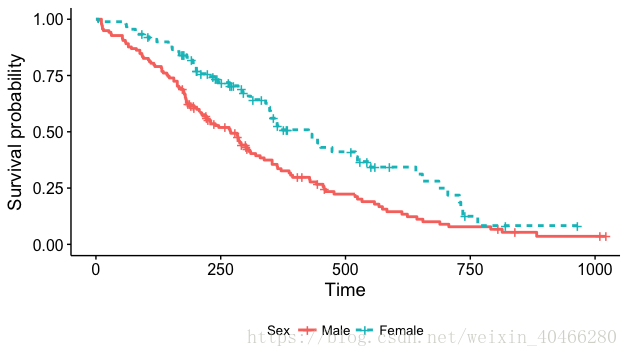
对比可以看出,survminer包绘制的生存曲线更加美观。同样,我们还可以对图形进行颜色的改变,图形大小的改变,增加图标以及图例位置的更换等:
ggsurvplot(km_2,
legend = "bottom", #将图例移动到下方
legend.title = "Sex",#改变图例名称
legend.labs = c("Male", "Female"),
linetype = "strata"# 改变线条类型
)- 1
- 2
- 3
- 4
- 5
- 6
修改后的图形:
3.比较分析
一般情况下,我们都需要比较分析两组的生存时间分布是否不同。在survival包中,有一个survdiff的函数可以进行long-rank检验
> survdiff(fit.surv~sex,data = lung,
rho = 0 # rho = 0 表示使用long-rank检验或者Mantel-Haenszel 检验)
Call:
survdiff(formula = fit.surv ~ sex, data = lung, rho = 0)
N Observed Expected (O-E)^2/E (O-E)^2/V
sex=1 138 112 91.6 4.55 10.3
sex=2 90 53 73.4 5.68 10.3
Chisq= 10.3 on 1 degrees of freedom, p= 0.00131
> - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
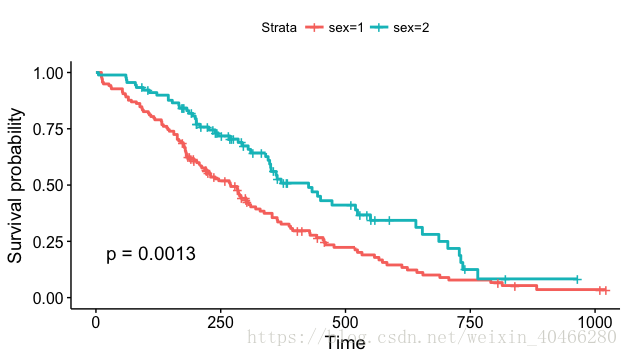
此外,可以使用survminer包中的ggsurvplot函数中的pval=TRUE参数,在生存曲线中添加P值:
ggsurvplot(km_2, main = "Survival curve",
pval=TRUE #添加P值
)- 1
- 2
- 3
4.Cox 回归模型
4.1 Cox 模型的建立
我们还是利用第二部分所用的肺癌数据集(lung)进行Cox回归模型的建立,这一次,我们感兴趣的点主要是年龄、体重减轻以及性别是否会影响肺癌的生存时间:
> library(survival)
> res.cox<-coxph(Surv(time,status)~age+ph.ecog+wt.loss,data = lung)
> res.cox
Call:
coxph(formula = Surv(time, status) ~ age + ph.ecog + wt.loss,
data = lung)
coef exp(coef) se(coef) z p
age 0.01347 1.01356 0.00974 1.38 0.16659
ph.ecog 0.47222 1.60356 0.12771 3.70 0.00022
wt.loss -0.00717 0.99285 0.00663 -1.08 0.27921
Likelihood ratio test=19 on 3 df, p=0.000269
n= 213, number of events= 151
(15 observations deleted due to missingness)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
在这个模型中我们可以看到ECOG评分的P值<0.01,认为在这个模型中能够显著影响肺癌的生存分析,OR=1.6。
4.2 模型诊断——PH检验
在构建Cox模型之后,我们需要对这个模型进行PH检验。如果无法通过PH检验,我们需要对上述的Cox模型进行修改。
在survival包中,函数cox.zph可进行PH检验:
cox.zph(res.cox)
rho chisq p
age -0.03663 0.22364 0.636
ph.ecog -0.08018 1.20971 0.271
wt.loss -0.00191 0.00064 0.980
GLOBAL NA 1.95904 0.581
> - 1
- 2
- 3
- 4
- 5
- 6
- 7
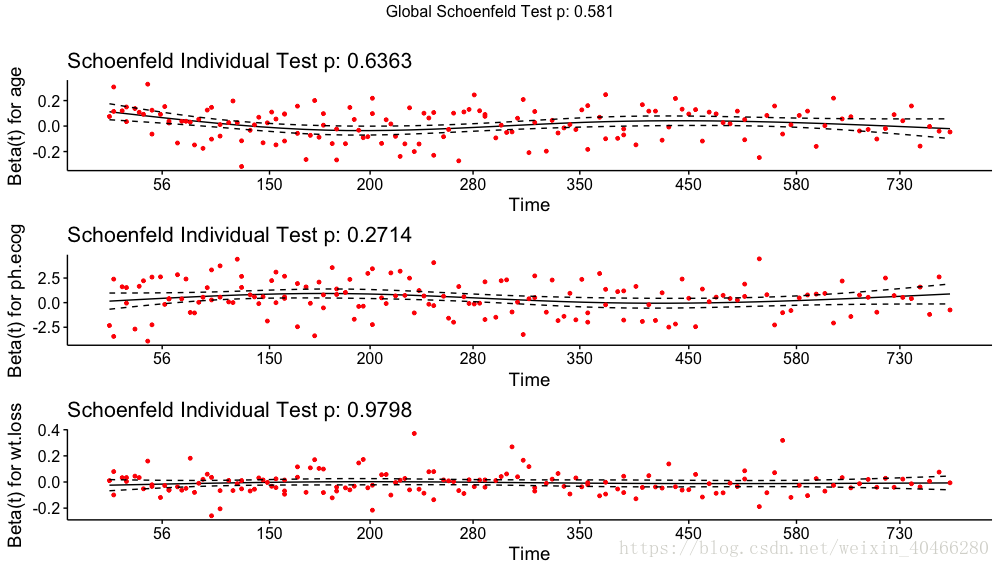
可以看到P 值都>0.01,说明该模型能够通过PH检验。
使用survminer包中的ggcoxzph函数还可以将其进行可视化:
> temp<-cox.zph(res.cox)
> ggcoxzph(temp)- 1
- 2
如果无法通过PH检验,可以进行分层或使用其他的检验方法,如参数检验等。