一、数学期望
首先明白一点:到达某个结果的期望值 = 这个结果 * 从起始状态到这个状态的概率
什么意思呢?
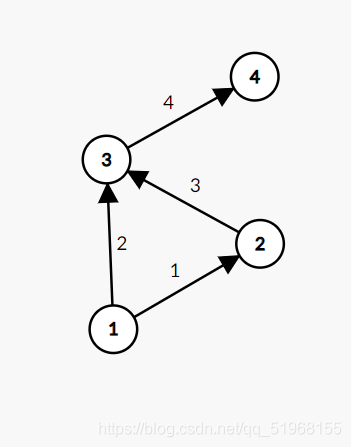
如图:
我们计算从\(1\)号点到\(3\)号点的期望距离
路径\(1\). \(\displaystyle 1−>3:E_1=2×\frac{1}{2}=1\)
路径\(2\). \(\displaystyle 1−>2−>3:E_2=1×\frac{1}{2}+3×\frac{1}{2}=2\)
这里路径\(2\)中从\(1\)到\(2\)概率为\(\displaystyle \frac{1}{2}\),但单看从\(2\)到\(3\)概率就是\(1\),但是从\(1\)到\(3\)那就是从(\(1\)到\(2\)的概率)\(\displaystyle \frac{1}{2}\)×\(1\)(\(2\)到\(3\)的概率)=\(\displaystyle \frac{1}{2}\)。
总结:概率是要叠乘的
这题是有正推和倒推两种写法的。
知道上面的东西之后那么我们就可以来搞正推的写法了
二、正推法
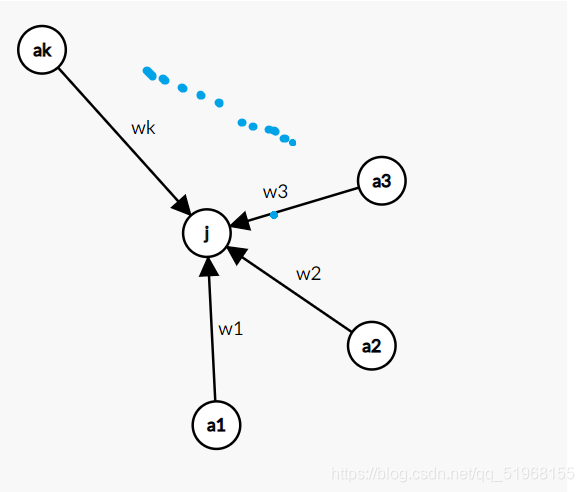
设:\(a_1, a_2, a_3 … a_k\) 到 \(j\) 的权值为 \(w_1, w_2, w_3 … w_k\),
从起点到这\(k\)个点的概率为:\(p_1, p_2, p_3 … p_k\)
每个点的出度为:\(out_1, out_2, out_3, … , out_k\)
这里的\(1\sim k\)个点的从起点的到该点的概率一定是确定的也就是说这个点的概率是被更新完的,即此时这个点的入度为\(0\)!
那么就有:
以上即是正推的递推式
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
//邻接表
int h[N], e[M], ne[M], w[M], idx;
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int n, m; // n个顶点,m条边
int out[N], in[N]; //出度,入度
double f[N], p[N]; // f:数学期望结果 p:概率
void topsort() {
queue<int> q;
//起点为1,起点的概率为100%
q.push(1), p[1] = 1;
// DAG,执行拓扑序,以保证计算的顺序正确,确保递归过程中,前序数据都已处理完毕
while (q.size()) {
auto t = q.front();
q.pop();
for (int i = h[t]; ~i; i = ne[i]) { //枚举的是每边相邻边
int j = e[i]; //此边,一端是t,另一端是j
//此边边条w[i]
f[j] += 1.0 * (w[i] * p[t] + f[t]) / out[t];
p[j] += 1.0 * p[t] / out[t]; // p[j]也需要概率累加
//拓扑序的标准套路
in[j]--;
if (!in[j]) q.push(j);
}
}
}
int main() {
//初始化邻接表
memset(h, -1, sizeof h);
cin >> n >> m;
while (m--) {
int a, b, c;
cin >> a >> b >> c;
add(a, b, c);
//维护出度,入度
out[a]++, in[b]++;
}
//拓扑序
topsort();
//正向递推,输出结果,保留两位小数
printf("%.2lf", f[n]);
return 0;
}
三、倒推法
现在学会了正推,那么咱们来看看逆推,即从终点找到起点
我们令:\(f(i)\)表示从\(i\)到\(n\)的期望距离,那么想要的答案即\(f(1)\)
如图:点\(\large j\)(右上角)通过\(x_1,x_2,x_3,… , x_k\)到\(n\), 点\(j\)到这\(k\)个点的距离为:\(w_{x1}, w_{x2}, w_{x3} ,… , w_{xk}\)
这\(k\)个点到\(n\)点的期望距离分别为\(\large f_{x1}, f_{x2}, f_{x3}, … , f_{xk}\)
\(out_j\):表示\(j\)的出度,\(\displaystyle \frac{1}{out_j}\):即为\(j\)到这\(k\)个点的概率

那么我们会有:
根据递推式我们可以看出我们想求\(f(j)\),那我们要求与\(j\)相连的点,而求这些相邻的点则要求这些点相邻的点,你是不是发现,这是个递归回溯的过程,所以我们可以记忆化搜索来解。
关于式子中一个疑惑的解答
咱们先看\(j\)到\(x_k\)的这条路径的柿子:\(\displaystyle f(j)+=\frac{f_{x_k}+w_{x_k}}{out_j}\)
这里\(\displaystyle \frac{w_{x_k}}{out_j}\)我理解不就是\(j\)到\(x_k\)的概率乘路径权值嘛,但是\(\displaystyle \frac{f_{x_k}}{out_j}\)这个\(x_k\)的期望也要乘\(j\)的概率呀??
来来来,看这里:咱们一开始就说了,从某个点到某个点的概率是会叠乘的,我们来看看式子中都表示什么含义:
\(f(x_k)\):仅表示从\(x_k\)到\(n\)的期望距离,不包含\(j\)这个点到\(x_k\)这个点概率的影响
\(f(j)\):从\(j\)到\(n\)的期望距离,而在路径上是会经过\(x_1,x_2,…,x_k\)这些点的
所以我们在求\(f(j)\)的时候要将\(j\)到\(x_k\)点概率的影响加到\(f(x_k)\)上面即:\(\displaystyle f(j)=+ \frac{f_{x_k}+w_{x_k}}{out_j}\)
综上:我们使用逆推记忆化搜索的递推式应为:
实现代码
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10, M = 2 * N;
int out[N]; //出度
double f[N]; //期望数组
//邻接表
int h[N], e[M], ne[M], w[M], idx;
void add(int a, int b, int c) {
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx++;
}
int n, m; // n个顶点,m条边
double dfs(int u) {
if (f[u] >= 0) return f[u]; //记忆化,算过不再算
f[u] = 0; //表示计算过
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i];
f[u] += (dfs(j) + w[i]) / out[u];
}
return f[u];
}
int main() {
cin >> n >> m;
memset(h, -1, sizeof h);
memset(f, -1, sizeof f);
int a, b, c;
while (m--) {
cin >> a >> b >> c;
add(a, b, c);
out[a]++; //维护出度
}
// base case 边界
f[n] = 0;
dfs(1);
// f[1]就是答案
printf("%.2lf", f[1]);
return 0;
}