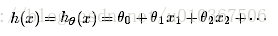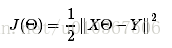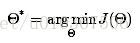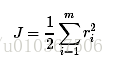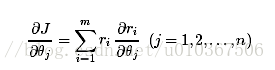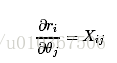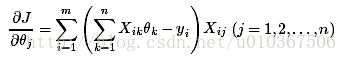梯度下降算法（Gradient Descent)

近期在搞论文，须要用梯度下降算法求解，所以又一次整理分享在这里。

主要包含梯度介绍、公式求导、学习速率选择、代码实现。

梯度下降的性质：

1.求得的解和选取的初始点有关

2.能够保证找到局部最优解，由于梯度终于会减小为0，则步长与梯度的乘积会自己主动越来越小。

梯度简单介绍

一个多元函数的在某点的梯度方向是函数值在该点增长最快的方向。即方向导数取最大值的方向。

问题描写叙述公式求导学习率选择

如果要学习这么一个函数：

那么损失函数能够定义成：

当中X矩阵，每行表示一个数据点，theta是列向量。Y也是列向量。

像这样的优化问题有非常多方法，那咱们先直接求导吧，对于求导过程。好多还是不理解。能够用这样的方法：

首先定义损失变量：

那么损失函数就能够表示成：

一步一步的求导：

再求：                             

                                                                               

那么把分步骤合起来就是：

能够用最小二乘或者梯度下降来求解，这里我们看看梯度下降的实现，梯度下降的思想不难。仅仅要确定好梯度以及梯度的方向就ok。由于是梯度的反方向去下降，所以在对參数更新的时候要注意：

下降速率能够从0.01開始尝试，越大下降越快，收敛越快。当然下降的速率能够改成自适用的。就是依据梯度的强弱适当调整步伐，这样效果还好一点儿。

代码

matlab实现

clc;
clear
% load data
heart_scale = load('heart_scale');
X = heart_scale.heart_scale_inst;
Y = heart_scale.heart_scale_label;
 
epsilon = 0.0003;
gamma= 0.0001;
 
w_old=zeros(size(X,2),1);%參数初始值均设为0
k=1;
figure(1);
while 1
minJ_w(k) = 1/2 * (norm(X*w_old - Y))^2;
w_new = w_old - gamma*(X'*X*w_old - X'*Y);
fprintf('The %dth iteration, minJ_w = %f, 
',k,minJ_w(k));
 
if norm(w_new-w_old) < epsilon %这里採用两次迭代中优化目标是否变化来判定是否收敛，也能够通过判定优化函数值是否变化来判定是否收敛
W_best = w_new;
break;
end
w_old = w_new;
k=k+1;
end
 
plot(minJ_w);%观察收敛性