教学之Treap

放在前面的话

本蒟蒻因为最近的题目总是搞点奇奇怪怪的平衡树，就去学了下(Treap)
现在来总结一下
由于本人是个蒟蒻，本文可能有部分错误，麻烦各位读者大佬在评论区提醒

什么是(Treap)

(Treap)取自两个单词，一是(tree)，一是(heap)
也就是说，(Treap)结合了二叉搜索树和堆

(Treap)维持平衡的方法

方法就是
随 机 数！！！
不要不信，真的是随机数
对于每个点，(Treap)给予它们一个随机数
并要求在满足二叉搜索树的基础上，随机数要形成一个大（小）根堆

---

接下来将给出一道模板题，(Treap)的操作将在模板题的讲解中给出

例题讲解

放例题

(Treap)例题

讲解

数组

(size[i])表示以(i)为根的子树的大小
(num[i])表示值为(i)的个数
(val[i])表示节点(i)的值
(son[i][0/1])表示(i)的左/右儿子
(rd[i])表示节点(i)的随机值
这些数组在接下来会多次提及，各位读者大佬可以稍稍记忆一下

操作

统计((pushup))

重新统计以(i)为根的子树的大小
当前大小：左儿子的大小+右儿子的大小+当前这个数的个数

void pushup(int p)
{
    size[p]=size[son[p][0]]+size[son[p][1]]+num[p];
}

旋转((rot))！！！

(Treap)的核心操作
分为左旋和右旋，但是思路一样，故一起介绍
旋转的目的是将一个子节点移到父亲处，在过程中满足二叉搜索树的性质
以右旋为例
一开始是这样的

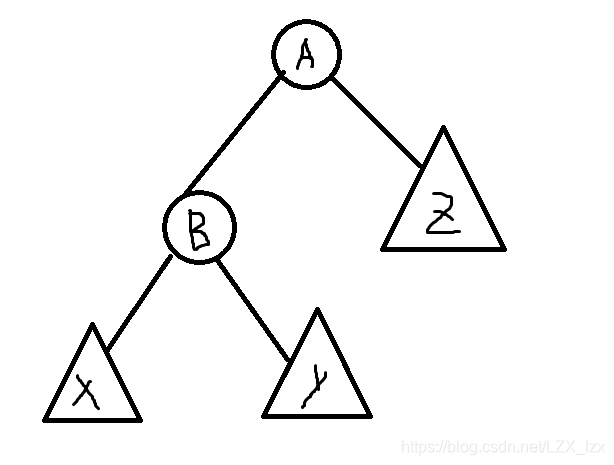
现在我们要将(B)转到(A)那里
怎么搞呢？？？
根据二叉搜索树的性质我们知道
(B<A)
那么可以把(A)丢给(B)当右儿子
但是(B)已经有了右儿子(y)了
再想，根据二叉搜索树有(B<y<A)
那么(y)就可以丢给(A)当左儿子
然后(B)的左儿子和(A)的右儿子不变
旋转完了之后

检查一下大小关系
旋转前：(x<B<y<A<z)
旋转后：(x<B<y<A<z)
一模一样
具体操作呢
上代码

void rot(int &p,int d)
{
    int k=son[p][d^1];
    son[p][d^1]=son[k][d];
    son[k][d]=p;
    pushup(p);
    pushup(k);
    p=k;
}

(d)为0是左旋，为1右旋
以(d=1)为例（右旋）

     a
    / 
   b   z
  / 
 x   y

(k)为(p)的左儿子
先把(k)的右儿子丢给(p)当左儿子：

son[p][d^1]=son[k][d];

现在长这样

              a(p)
             / 
   b(k)     y   z
  / 
 x   

再把(p)丢给(k)当右儿子

son[k][d]=p;

变成了这样

     b(k)
    / 
   x   a(p)
      / 
     y   z

再(pushup(p和k))
最后(p=k)
结束
那么我们就可以用旋转来维护堆了

插入((ins))

要插入一个数(x)
可以一直判断(x)与当前节点的大小关系，选择往哪边递归
直到找到一棵空子树就把(x)放进去
放进去之后看一下(rd)值的大小，有不对的就旋转
插入后重新统计大小

void ins(int &p,int x)
{
    if (!p)
    {
        sum++;
        p=sum;
        size[p]=num[p]=1;
        val[p]=x;
        rd[p]=rand();
        return;
    }
    if (val[p]==x)
    {
        num[p]++;
        size[p]++;
        return;
    }
    int d=(x>val[p]);
    ins(son[p][d],x);
    if (rd[p]<rd[son[p][d]]) rot(p,d^1);
    pushup(p);
}

删除((del))

跟插入差不多
(x<val[p])往左边走
(x>val[p])往右边走
有点不同的是在(x=val[p])的时候
分4种情况讨论

1. 无左儿子和右儿子
2. 无左儿子
3. 无右儿子
4. 有左儿子和右儿子

情况1：删自己
情况2：左旋，往左边走
情况3：右旋，往右边走
情况4：看哪边的(rd)值大，就旋转哪边，往那边走
删除完之后重新统计一下大小

void del(int &p,int x)
{
    if (!p) return;
    if (x<val[p]) del(son[p][0],x);
    else if (x>val[p]) del(son[p][1],x);
    else
    {
        if (!son[p][0]&&!son[p][1])
        {
            num[p]--;
            size[p]--;
            if (!num[p]) p=0;   
        }
        else if (!son[p][1])
        {
            rot(p,1);
            del(son[p][1],x);
        }
        else if (!son[p][0])
        {
            rot(p,0);
            del(son[p][0],x);
        }
        else
        {
            int d=(rd[son[p][0]]>rd[son[p][1]]);
            rot(p,d);
            del(son[p][d],x);
        }
    }
    pushup(p);
}

查询排名((get\_rank))

如果没有这个数，返回0
如果(val[p]=x)，输出左儿子的大小+1
如果(val[p]>x)，往左儿子走
如果(val[p]<x)，往右儿子走，并输出左儿子的大小+(num[x])+(x)在右儿子中的排名

int get_rank(int p,int x)
{
    if (!p) return 0;
    if (val[p]==x) return (size[son[p][0]]+1);
    if (val[p]<x) return (size[son[p][0]]+num[p]+get_rank(son[p][1],x));
    if (val[p]>x) return get_rank(son[p][0],x);
}

查询值((get\_sum))

如果(size[son[p][0]>x) 往左边走
如果(size[son[p][0]+num[p]<x) 往右边走，在右边查找排名(x-size[son[p][0]-num[p])的数
若都不满足，返回(val[p])

int get_sum(int p,int x)
{
    if (!p) return 0;
    if (size[son[p][0]]>=x) return get_sum(son[p][0],x);
    else if (size[son[p][0]]+num[p]<x)  return get_sum(son[p][1],x-size[son[p][0]]-num[p]);
    else return val[p];
}

查询前驱((get\_pre))

如果当前(p)为0返回(-∞)（一定要特别小）
如果(val[p]>=x)，即在左儿子中，那就往左边走
否则的话返回当前值和右儿子中的前驱里大的那个（所以为什么要特别小）

int get_pre(int p,int x)
{
    if (!p) return -inf;
    if (val[p]>=x) return get_pre(son[p][0],x);
    else return max(val[p],get_pre(son[p][1],x));
}

查询后继((get\_suc))

跟查询前驱类似
只不过为0的时候返回(∞)，因为后面是(min)
左儿子和右儿子换一下就可以

int get_suc(int p,int x)
{
    if (!p) return inf;
    if (val[p]<=x) return get_suc(son[p][1],x);
    else return min(val[p],get_suc(son[p][0],x));
}

---

到此所有的操作都已讲解完毕

Code——总

#include<cstdio>
#include<stdlib.h>
#include<iostream>
#define inf 2147483647
using namespace std;
int n,pd,x,s,sum,size[100005],son[100005][3],val[100005],num[1000005],rd[100005];
void pushup(int p)
{
    size[p]=size[son[p][0]]+size[son[p][1]]+num[p];
}
void rot(int &p,int d)
{
    int k=son[p][d^1];
    son[p][d^1]=son[k][d];
    son[k][d]=p;
    pushup(p);
    pushup(k);
    p=k;
}
void ins(int &p,int x)
{
    if (!p)
    {
        sum++;
        p=sum;
        size[p]=num[p]=1;
        val[p]=x;
        rd[p]=rand();
        return;
    }
    if (val[p]==x)
    {
        num[p]++;
        size[p]++;
        return;
    }
    int d=(x>val[p]);
    ins(son[p][d],x);
    if (rd[p]<rd[son[p][d]]) rot(p,d^1);
    pushup(p);
}
void del(int &p,int x)
{
    if (!p) return;
    if (x<val[p]) del(son[p][0],x);
    else if (x>val[p]) del(son[p][1],x);
    else
    {
        if (!son[p][0]&&!son[p][1])
        {
            num[p]--;
            size[p]--;
            if (!num[p]) p=0;   
        }
        else if (!son[p][1])
        {
            rot(p,1);
            del(son[p][1],x);
        }
        else if (!son[p][0])
        {
            rot(p,0);
            del(son[p][0],x);
        }
        else
        {
            int d=(rd[son[p][0]]>rd[son[p][1]]);
            rot(p,d);
            del(son[p][d],x);
        }
    }
    pushup(p);
}
int get_rank(int p,int x)
{
    if (!p) return 0;
    if (val[p]==x) return (size[son[p][0]]+1);
    if (val[p]<x) return (size[son[p][0]]+num[p]+get_rank(son[p][1],x));
    if (val[p]>x) return get_rank(son[p][0],x);
}
int get_sum(int p,int x)
{
    if (!p) return 0;
    if (size[son[p][0]]>=x) return get_sum(son[p][0],x);
    else if (size[son[p][0]]+num[p]<x)  return get_sum(son[p][1],x-size[son[p][0]]-num[p]);
    else return val[p];
}
int get_pre(int p,int x)
{
    if (!p) return -inf;
    if (val[p]>=x) return get_pre(son[p][0],x);
    else return max(val[p],get_pre(son[p][1],x));
}
int get_suc(int p,int x)
{
    if (!p) return inf;
    if (val[p]<=x) return get_suc(son[p][1],x);
    else return min(val[p],get_suc(son[p][0],x));
}
int main()
{
    freopen("104.in","r",stdin);
    scanf("%d",&n);
    while (n--)
    {
        scanf("%d%d",&pd,&x);
        if (pd==1) ins(s,x);
        if (pd==2) del(s,x);
        if (pd==3) printf("%d
",get_rank(s,x));
        if (pd==4) printf("%d
",get_sum(s,x));
        if (pd==5) printf("%d
",get_pre(s,x));
        if (pd==6) printf("%d
",get_suc(s,x));
    }
    return 0;
}