根据题意,我已经推导出tn的公式,ti=ti.a+ti.b,ti.a=5*t(i-1).a+4*t(i-1).b,ti.b=t(i-1).a+t(i-1).b
然而下面竟然不能继续推到sn的公式!!!!
这道题考察的就是求任意数列的前n项和,在sn的递推公式不太明显的时候,用矩阵解决。
设矩阵A= ,矩阵F0=
,矩阵F0=
那么设矩阵S=(A+A2+A3…. + An)*F0
最终答案就是矩阵S内两个元素之和。
那么怎么求A+A2+A3…. + An ?
可以继续构造如下的分块矩阵,其中 I 是单位矩阵
设R= ,则有: R2=
,则有: R2= ,R3=
,R3=
可以发现右上角即为 I + A + A^2 + ... + A^n,多一个 I 后面给减掉就可以了
可以用快速幂求出R^n;
然而上面的方法对于此题仍然tle,看了标码发现,能通过推导进一步缩小矩阵的阶数,我这里的R是四阶,而标码里的运算只有三阶。
继续思考:
看看能不能直接推导得到S的通项公式,看讲解:
T[i] = dp[i][0]+dp[i][1]
=6*dp[i-1][1]+5*dp[i-1][0]
=6*T[i-1]-dp[i-1][0]
=6*T[i-1]-T[i-2]
根据S[i]=S[i-1]+T[i]可以计算出:
S[i]=S[i-1]+ 6*T[i-1]-T[i-2]
则有公式:

设R= 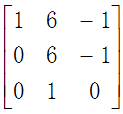 ,搞定!
,搞定!
总结:矩阵的应用,仔细学习上面的构造矩阵和推导过程,第一种构造分块矩阵的方法很有用,它对sn公式不好直接构造矩阵的时候适用。但如果像上面S[i]=S[i-1]+ 6*T[i-1]-T[i-2]这样的公式可以推导出sn的递推矩阵,可以降低复杂度。
#include<stdio.h> #include<cstring> #include<cmath> #include<algorithm> #include<queue> using namespace std; const long long mod = 1000000007; struct Ma { long long m[3][3]; }; Ma operator * (Ma a,Ma b) { Ma c; for(int i=0; i<3; i++) for(int j=0; j<3; j++) { c.m[i][j] = 0; for (int k = 0; k < 3; k++) { c.m[i][j]+=(a.m[i][k]*b.m[k][j]); if(c.m[i][j]>=mod||c.m[i][j]<=-mod) c.m[i][j]%=mod; //c.m[i][j]%=mod; } } return c; } Ma mm[65]; long long cal(long long n) { int cur=0; Ma ans= {1,6,-1, 0,6,-1, 0,1,0 }; while(n) { if(n&1) { ans = ans*mm[cur]; } cur++; n>>=1; } long long tmp=41*ans.m[0][0]%mod+35*ans.m[0][1]%mod+6*ans.m[0][2]%mod+mod; tmp%=mod; while(tmp<0) tmp+=mod; printf("%lld ",tmp); return tmp; } //long long ans[10000005]; int main() { Ma tmp= {1,6,-1, 0,6,-1, 0,1,0 }; mm[0] = tmp; for(int i=1; i<64; i++) mm[i]=mm[i-1]*mm[i-1]; long long n; while(scanf("%lld",&n)!=EOF) { if(n==1) puts("6"); else if(n==2) puts("41"); else cal(n-3); } return 0; }