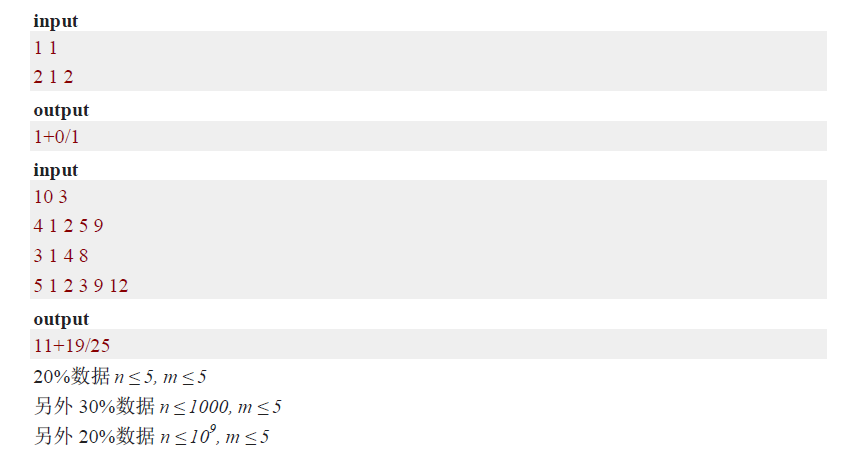http://codeforces.com/gym/100240 J
【分析】
这题我搞了好久才搞出样例的11.76。。。。【期望没学好
然后好不容易弄成分数形式。然后我‘+’没打。。【于是爆0。。。
好桑心。。
对于x^2这样的期望,是不能直接求x的期望然后平方的!
为什么呢?因为意义就是不对的,你的概率有可能乘了两次什么的。。。
我的方法是:
先把每天分离出来,对于某一天,假设你前i部番的x^2的期望求了出来,然后新的一部翻在这天放的概率是p,
新的答案就是$x^{2}*(1-p)+p*(x+1)^2$
即$x^{2}+p*(2*x+1)$
这样就可以求了。【实测是对的啊!!
所以你还要维护x的期望【这个很容易的啦。
然后你会发现,你的分数是a/(n^2)+b/n,这种形式的,a很小不会超过n,我就用两个东西来存这两个分子。
每超过分母就把它加进整数部分,这样用long long就不会爆了。
对于n很大,发现d<=10000,dmx~n这一段的期望其实是完全一样的,所以只需要求1~dmx就好了。
如果d也很大的话,还可以把d离散,中间的点的期望跟前面最近的点的期望是一样的。
男神的方法好像有点不一样?但是我觉得这个更容易想啊!

1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<iostream> 5 #include<algorithm> 6 using namespace std; 7 #define Maxn 10010 8 #define LL long long 9 10 int b[110][110]; 11 LL d[Maxn],c[Maxn]; 12 int mymax(LL x,LL y) {return x>y?x:y;} 13 14 struct node 15 { 16 LL x,y,z; 17 }A[Maxn]; 18 19 LL gcd(LL a,LL b) 20 { 21 if(b==0) return a; 22 return gcd(b,a%b); 23 } 24 25 LL n; 26 void add(LL x,LL a,LL b) 27 { 28 A[x].x+=a;A[x].y+=b; 29 A[x].z+=A[x].x/(n*n);A[x].z+=A[x].y/n; 30 A[x].x%=(n*n);A[x].y%=n; 31 } 32 33 int main() 34 { 35 int m,mx=0; 36 scanf("%lld%d",&n,&m); 37 for(int i=1;i<=m;i++) 38 { 39 scanf("%d",&b[i][0]); 40 for(LL j=1;j<=b[i][0];j++) 41 { 42 scanf("%d",&b[i][j]); 43 mx=mymax(mx,b[i][j]); 44 } 45 } 46 for(int i=0;i<=mx;i++) A[i].x=0,A[i].y=0,A[i].z=0; 47 for(int i=1;i<=mx;i++) c[i]=0; 48 for(int i=1;i<=m;i++) 49 { 50 for(int j=1;j<=mx;j++) d[j]=0; 51 for(int j=1;j<=mx;j++) 52 { 53 for(int k=1;k<=b[i][0];k++) 54 { 55 if(j+b[i][k]-1>mx) break; 56 d[j+b[i][k]-1]++; 57 } 58 } 59 for(int i=1;i<=mx;i++) 60 { 61 add(i,d[i]*2*c[i],d[i]); 62 c[i]+=d[i]; 63 } 64 } 65 if(n<=mx) 66 { 67 for(int i=1;i<=n;i++) 68 { 69 A[0].z+=A[i].z; 70 add(0,A[i].x,A[i].y); 71 } 72 } 73 else 74 { 75 for(int i=1;i<=mx;i++) 76 { 77 A[0].z+=A[i].z; 78 add(0,A[i].x,A[i].y); 79 } 80 A[0].z+=(n-mx)*A[mx].z; 81 add(0,A[mx].x*(n-mx),A[mx].y*(n-mx)); 82 } 83 A[0].x+=A[0].y*n; 84 A[0].z+=A[0].x/(n*n); 85 A[0].x%=(n*n); 86 LL g=gcd(A[0].x,n*n); 87 A[0].x/=g;A[0].y=n*n/g; 88 printf("%lld+%lld/%lld ",A[0].z,A[0].x,A[0].y); 89 return 0; 90 }
2017-04-19 10:16:51