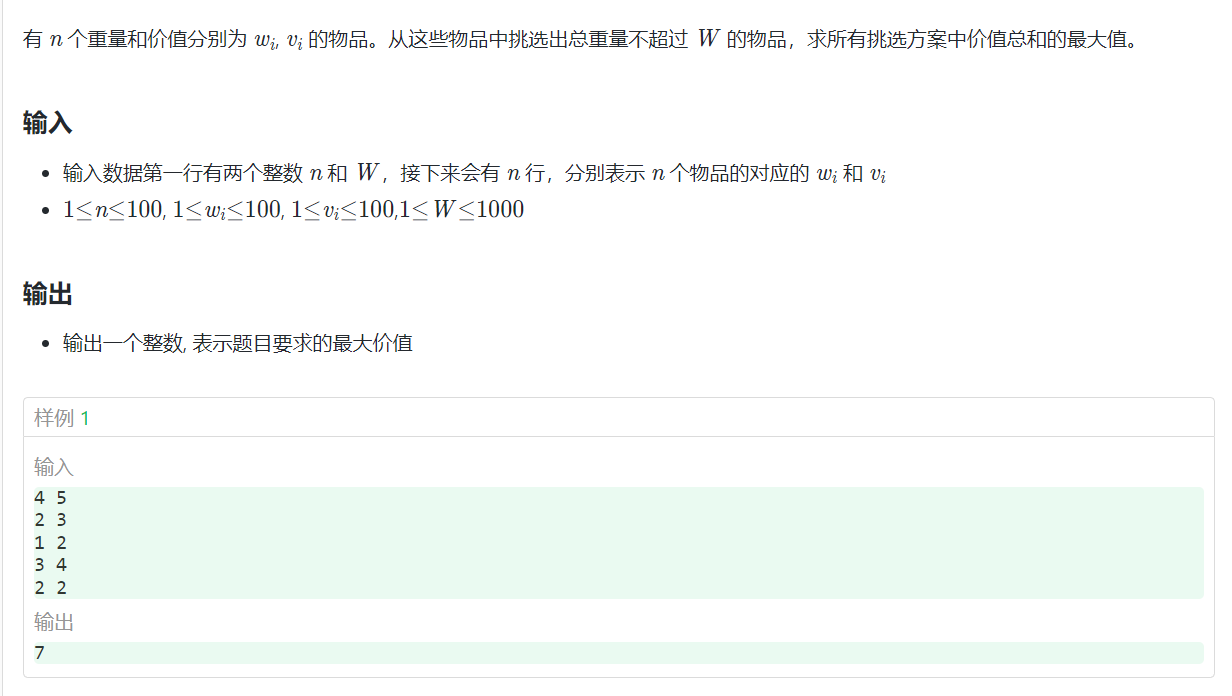
地址 https://www.papamelon.com/problem/218
经典的动态规划问题。
网络搜索背包九讲可以找到详细的文字和视频题解
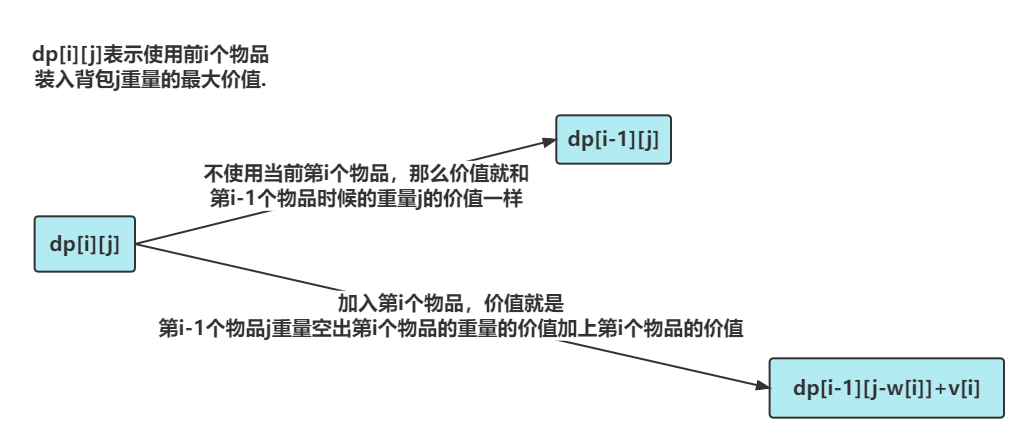
dp[i][j]表示使用前i个物品装入背包j重量的最大价值.
本题状态转移方程
dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+v[i])
dp[i][j] = dp[i-1][j]
表示不选择第i个物品 那么装入j重量物品的最大价值就是选择前i-1个物品装入j重量时的最大价值
dp[i][j]=dp[i-1][j-w[i]]+v[i]
表示选择第i个物品,由于装入的物品的重量是j
那么状态只能从 j-w[i]的重量转移过来,选择了第i个物品,所以最大价值要加上v[i]
两种情况 dp[i][j]选择最大值.
代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1010;
int dp[N][N];
int w[N];
int v[N];
int n, W;
/*
输入
4 5
2 3
1 2
3 4
2 2
输出
7
*/
int main()
{
cin >> n >> W;
for (int i = 1; i <= n; i++) {
cin >> w[i] >> v[i];
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j <= W; j++) {
dp[i][j] = dp[i - 1][j];
if(j>=w[i])
dp[i][j] = max(dp[i][j],dp[i-1][j-w[i]]+v[i]);
}
}
cout << dp[n][W] << endl;
return 0;
}

