该补一下以前挖的坑了
先总结一下
第二次

T1 搜索+剪枝

1 #include<cstdio> 2 #include<iostream> 3 #define ll long long 4 using namespace std; 5 const int maxn=8005; 6 int a[maxn],n,js[maxn]; 7 bool jk[maxn]; 8 ll ans; 9 bool judge(int l,int r) 10 { 11 int i=l; 12 while(i<r) 13 { 14 if(a[i]+1!=a[i+1])return 0; 15 else i++; 16 } 17 return 1; 18 } 19 void out() 20 { 21 for(int i=1;i<=(1<<n);i++) 22 { 23 cout<<a[i]<<" "; 24 } 25 cout<<endl; 26 } 27 void search(int num,int last) 28 { 29 //out();//cout<<"->"<<endl; 30 if(judge(1,1<<n)){ans+=js[num];return ;} 31 if(last==n+1)return ; 32 int must1=0,must2=0; 33 for(int j=1;j<=(1<<n);j+=(1<<last)) 34 { 35 if(!judge(j,j+(1<<last)-1)&&!must1)must1=j; 36 else if(!judge(j,j+(1<<last)-1)&&must1&&!must2)must2=j; 37 else if(!judge(j,j+(1<<last)-1))return ; 38 } 39 if(!must1&&!must2)search(num,last+1); 40 else if(!must2) 41 { 42 int j=must1,k=must1+(1<<(last-1)); 43 int kx=0; 44 while(kx<(1<<(last-1))) 45 { 46 swap(a[j+kx],a[k+kx]); 47 kx++; 48 } 49 search(num+1,last+1); 50 kx=0; 51 while(kx<(1<<(last-1))) 52 { 53 swap(a[j+kx],a[k+kx]); 54 kx++; 55 } 56 return ; 57 } 58 else 59 { 60 int jj[2]={},kk[2]={}; 61 // cout<<must1<<" "<<must2<<endl; 62 jj[0]=must1,jj[1]=must1+(1<<(last-1)); 63 kk[0]=must2,kk[1]=must2+(1<<(last-1)); 64 //cout<<jj[1]<<" "<<kk[1]<<endl; 65 for(int i=0;i<=1;i++) 66 for(int j=0;j<=1;j++) 67 { 68 //out(); 69 //cout<<jj[i]<<" "<<kk[j]<<endl; 70 int kx=0; 71 while(kx<(1<<(last-1))) 72 { 73 swap(a[jj[i]+kx],a[kk[j]+kx]); 74 kx++; 75 } 76 search(num+1,last+1); 77 kx=0; 78 while(kx<(1<<(last-1))) 79 { 80 swap(a[jj[i]+kx],a[kk[j]+kx]); 81 kx++; 82 } 83 84 } 85 } 86 return ; 87 } 88 int main() 89 { 90 scanf("%d",&n); 91 js[1]=1; 92 for(int i=2;i<=n;i++) 93 js[i]=js[i-1]*i; 94 for(int i=1;i<=(1<<n);i++) 95 { 96 scanf("%d",&a[i]); 97 } 98 search(0,1); 99 cout<<ans<<endl; 100 return 0; 101 }
T2 划艇 高难标记
31分算法:线段树优化DP
AC算法:
区间离散化。
跨区间显然,同区间组合计数。

1 #include<cstdio> 2 #include<iostream> 3 #include<algorithm> 4 #define mod DeepinC 5 #define maxn 505 6 using namespace std; 7 int l[maxn*2],len[maxn*2],sum[maxn*2][maxn*2],num[maxn*2][maxn*2],a[maxn],b[maxn],f[maxn][maxn*2],inv[maxn*10+5]; 8 const int mod=1e9+7; 9 int qpower(int a,int b) 10 { 11 int ans=1; 12 while(b) 13 { 14 if(b&1)ans=1ll*ans*a%mod; 15 b>>=1; 16 a=1ll*a*a%mod; 17 } 18 return ans; 19 } 20 void get_inv() 21 { 22 for(int i=1;i<=500;i++) 23 inv[i]=qpower(i,mod-2); 24 return ; 25 } 26 int main() 27 { 28 get_inv(); 29 int n,tot=0,ans=0; 30 scanf("%d",&n); 31 for(int i=1;i<=n;i++) 32 { 33 scanf("%d%d",&a[i],&b[i]); 34 b[i]++; 35 l[++tot]=a[i]; 36 l[++tot]=b[i]; 37 } 38 sort(l+1,l+tot+1); 39 tot=unique(l+1,l+tot+1)-l-1; 40 for(int i=1;i<tot;i++) 41 { 42 len[i]=l[i+1]-l[i]; 43 //cout<<i<<" "<<len[i]<<endl; 44 } 45 for(int i=1;i<=n;i++) 46 { 47 a[i]=lower_bound(l+1,l+tot+1,a[i])-l; 48 b[i]=lower_bound(l+1,l+tot+1,b[i])-l-1; 49 } 50 sum[0][0]=1; 51 for(int i=1;i<=n;i++) 52 { 53 sum[i][0]=1; 54 } 55 for(int j=1;j<=tot;j++)sum[0][j]=1; 56 for(int i=1;i<=n;i++) 57 { 58 for(int j=a[i];j<=b[i];j++) 59 { 60 f[i][j]=1ll*sum[i-1][j-1]*len[j]%mod; 61 // cout<<f[i][j]<<endl; 62 int o=1,C=(len[j]-1)%mod; 63 for(int k=i-1;k;k--) 64 { 65 if(a[k]>j||b[k]<j)continue; 66 o++; 67 C=1ll*C*(o+len[j]-2)%mod*inv[o]%mod; 68 //cout<<C<<endl; 69 f[i][j]=(f[i][j]+1ll*C*sum[k-1][j-1]%mod)%mod; 70 } 71 ///cout<<f[i][j]<<endl; 72 ans+=f[i][j]; 73 ans%=mod; 74 } 75 for(int j=1;j<=tot;j++) 76 sum[i][j]=((1ll*sum[i-1][j]+sum[i][j-1])%mod-sum[i-1][j-1]+f[i][j]+mod)%mod; 77 } 78 cout<<ans<<endl; 79 return 0; 80 }
T3 放棋子:DP
设g[i][j][k]表示用k个棋子填满i行j列的方案,设f[i][j][k]表示用前k种棋子填满i行j列的方案
容斥计算g数组: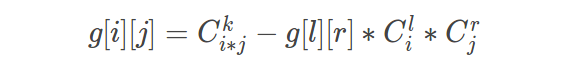
那么f数组 :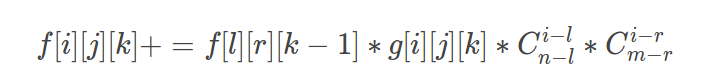
最终答案: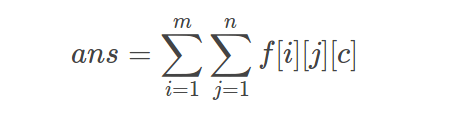
(图片来自https://www.cnblogs.com/yanshannan/p/9467292.html,特此鸣谢)
AC代码:

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #define maxn 35 5 using namespace std; 6 const int mod=1e9+9; 7 int C[maxn*maxn][maxn*maxn],g[maxn][maxn],f[maxn][maxn][maxn*maxn],cn[maxn]; 8 int moded(int x) 9 { 10 if(x<0)return x+mod; 11 return x>=mod?x-mod:x; 12 } 13 int main() 14 { 15 // freopen("out.txt","w",stdout); 16 int n,m,c,tot=0; 17 scanf("%d%d%d",&n,&m,&c); 18 for(int i=1;i<=c;i++) 19 { 20 scanf("%d",&cn[i]); 21 tot=max(tot,cn[i]); 22 } 23 for(int i=1;i<=900;i++) 24 { 25 C[i][0]=C[i][i]=1; 26 for(int j=1;j<i;j++) 27 C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod; 28 } 29 f[0][0][0]=1; 30 int ans=0; 31 for(int k=1;k<=c;k++) 32 { 33 memset(g,0,sizeof(g)); 34 for(int i=1;i<=n;i++) 35 for(int j=1;j<=m;j++) 36 { 37 g[i][j]=C[i*j][cn[k]]; 38 for(int ii=0;ii<=i;ii++) 39 for(int jj=0;jj<=j;jj++) 40 { 41 if(ii==i&&jj==j)continue; 42 g[i][j]=(g[i][j]-1ll*g[ii][jj]*C[i][ii]%mod*C[j][jj]%mod+mod)%mod; 43 } 44 //cout<<k<<" "<<i<<" "<<j<<" "<<" "<<g[i][j]<<endl; 45 } 46 for(int i=1;i<=n;i++) 47 for(int j=1;j<=m;j++) 48 { 49 for(int ii=0;ii<i;ii++) 50 for(int jj=0;jj<j;jj++) 51 { 52 f[i][j][k]=(f[i][j][k]+1ll*f[ii][jj][k-1]*C[n-ii][i-ii]%mod*C[m-jj][j-jj]%mod*g[i-ii][j-jj]%mod)%mod; 53 //if(k==c&&i==n&&j==m)cout<<ii<<" "<<jj<<" "<<f[ii][jj][k-1]<<endl; 54 } 55 if(k==c) 56 { 57 ans=moded(ans+f[i][j][c]); 58 //if(i==n)cout<<i<<" "<<j<<" "<<f[i][j][c]<<endl; 59 } 60 } 61 62 } 63 cout<<ans<<endl; 64 return 0; 65 }
第三次

爆零。。。
T1:序列
乱搞,(鬼知道我打了一个什么倍增)
AC代码:(不会告诉你我是QJ的)
感谢wd大佬的帮助%%DeepinC

1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 #include<cstring> 5 #define maxn 200005 6 #define maxq 1001 7 #include<vector> 8 #include<algorithm> 9 #define LL long long 10 #define ts puts("--------"); 11 using namespace std; 12 LL n,a[maxn],ans,need1[maxn],A[maxn],maxx,b[maxn][21],num[maxn],fr[maxn][21],Num[105],nuM[105],toty; 13 LL prime[maxq*10000+5],tot,frprime[maxq*10000+5]; 14 bool isnotprime[maxq*10000+5]; 15 LL gcd(LL a,LL b) 16 { 17 return b==0?a:gcd(b,a%b); 18 } 19 LL qpower(LL a,LL b) 20 { 21 LL ans=1; 22 while(b) 23 { 24 if(b&1)ans=ans*a; 25 a=a*a; 26 b>>=1; 27 } 28 return ans; 29 } 30 void pre() 31 { 32 for(int i=2;i<=maxq*10000;i++) 33 { 34 if(!isnotprime[i]) 35 { 36 prime[++toty]=i; 37 frprime[i]=i; 38 } 39 for(int j=1;j<=toty;j++) 40 { 41 if(i*prime[j]>maxq*10000)break; 42 isnotprime[i*prime[j]]=1; 43 frprime[i*prime[j]]=prime[j]; 44 if(!i%prime[j])break; 45 } 46 } 47 } 48 LL GetUse(LL x) 49 { 50 LL mt=x; 51 if(x%10==0){ 52 while(x%10==0)x/=10; 53 return x==1?10ll:mt; 54 } 55 if(x%7==0){ 56 while(x%7==0)x/=7; 57 return x==1?7ll:mt; 58 } 59 if(x%6==0){ 60 while(x%6==0)x/=6; 61 return x==1?6ll:mt; 62 } 63 if(x%5==0){ 64 while(x%5==0)x/=5; 65 return x==1?5ll:mt; 66 } 67 if(x%3==0){ 68 while(x%3==0)x/=3; 69 return x==1?3:mt; 70 } 71 if(x%2==0){ 72 while(x%2==0)x/=2; 73 return x==1?2:mt; 74 } 75 return mt; 76 } 77 bool query(LL st,LL len) 78 { 79 LL cnt=0; 80 for(LL i=st;i<=st+len-1;i++) 81 { 82 num[++cnt]=a[i]; 83 } 84 sort(num+1,num+cnt+1); 85 for(LL i=2;i<=cnt;i++)if(num[i]==num[i-1]){return 0;} 86 return 1; 87 } 88 LL Get(LL x,LL q) 89 { 90 if(q==1)return x; 91 while(x%q==0)x/=q; 92 return x; 93 } 94 bool judge(LL len) 95 { 96 LL Q=0,now,F; 97 for(LL i=1;i<=n-len+1;i++) 98 { 99 now=0;Q=0; 100 for(LL t=17;t>=1;t--) 101 { 102 if((1<<t)+now<=len){ 103 if(b[i+now][t]==-1){break;} 104 // cout<<i<<' '<<len<<' '<<t<<' '<<now<<" from "<<n-len+1<<endl; 105 if(!Q){Q=b[i+now][t];F=fr[i+now][t];} 106 else if(b[i+now][t]==-1||Q!=b[i+now][t]||fr[i+now][t]!=F){break;} 107 now+=(1<<t); 108 if(now==len){ 109 if(Q==1||query(i,len))return 1; 110 else break; 111 } 112 if(now==len-1){ 113 if(Q==1&&a[i+len-1]==a[i+len-2])return 1; 114 if(a[i+len-1]>a[i+len-2]&&query(i,len)&&a[i+len-1]%a[i+len-2]==0) 115 { 116 LL t=a[i+len-1]/a[i+len-2]; 117 if(GetUse(t)==Q)return 1; 118 } 119 else 120 if(a[i+len-1]<a[i+len-2]&&query(i,len)&&a[i+len-2]%a[i+len-1]==0) 121 { 122 LL t=a[i+len-2]/a[i+len-1]; 123 if(GetUse(t)==Q)return 1; 124 } 125 break; 126 } 127 } 128 } 129 } 130 return 0; 131 } 132 int main() 133 { 134 scanf("%lld",&n); 135 for(LL i=1;i<=n;i++)scanf("%lld",&a[i]); 136 for(LL i=2;i<=n;i++) 137 if(a[i]%a[i-1]==0){ 138 b[i-1][1]=a[i]/a[i-1]; 139 b[i-1][1]=GetUse(b[i-1][1]); 140 fr[i-1][1]=Get(a[i-1],b[i-1][1]); 141 } 142 else if(a[i-1]%a[i]==0){ 143 b[i-1][1]=a[i-1]/a[i]; 144 b[i-1][1]=GetUse(b[i-1][1]); 145 fr[i-1][1]=Get(a[i],b[i-1][1]); 146 } 147 else b[i-1][1]=-1; 148 b[n][1]=-1; 149 for(LL i=2;i<=17;i++) 150 for(LL j=1;j<=n;j++){ 151 if(b[j][i-1]==b[j+(1<<(i-1))][i-1]&&b[j][i-1]!=-1&&fr[j][i-1]==fr[j+(1<<(i-1))][i-1]) 152 b[j][i]=b[j][i-1],fr[j][i]=fr[j][i-1]; 153 else b[j][i]=-1; 154 } 155 LL l=2,r=n; 156 while(l<=r) 157 { 158 int mid=l+r>>1; 159 if(judge(mid)){ans=mid;l=mid+1;} 160 else r=mid-1; 161 } 162 cout<<ans<<endl; 163 return 0; 164 }
T2:熟练剖分
概率期望不是DP
值得一提的是,wq学长为我们证明了某种树DP复杂度(枚举深度,子树大小。。):设(x,y)表示树上的一对节点对,那么考虑每个节点的贡献,每个节点会被它的父链上的每个节点计算一次,所以每个节点被计算n次即总复杂度n×n。
还有很重要的是,打成相加形式才是n^2,不然是n^3
n^2
1 for(int j=size[x];j>=0;j--)
2 {
3 for(int k=0;k<=min(j,size[y]);k++)
4 {
5 f[x][j][1]=min(f[x][j][1],f[x][j-k][1]+f[y][k][1]);
6 f[x][j][0]=min(f[x][j][0],f[x][j-k][0]+min(f[y][k][0],f[y][k][1]));
7 }
8 }
n^3
1 for(int j=size[x];j>=0;j--)
2 {
3 for(int k=size[y];k>=0;k--)
4 {
5 f[x][j+k][1]=min(f[x][j+k][1],f[x][j][1]+f[y][k][1]);
6 f[x][j+k][0]=min(f[x][j+k][0],f[x][j][0]+min(f[y][k][0],f[y][k][1]));
7 }
8 }
这道题就是这一类
AC代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<vector> 4 #include<cstring> 5 using namespace std; 6 const int mod=1e9+7; 7 int n,indu[3100],root; 8 vector<int>son[3100]; 9 long long f[3100][3100],g[2][2][3100],dep[3100]; 10 long long pow(long long a,long long b){ 11 long long ans=1; 12 a%=mod; 13 while(b){ 14 if(b&1) ans=(ans*a)%mod; 15 b>>=1; 16 a=(a*a)%mod; 17 } 18 return ans%mod; 19 } 20 long long max(long long a,long long b){ 21 return a>b?a:b; 22 } 23 void dfs(int x){ 24 if(son[x].size()==0){ 25 f[x][0]=1; 26 //printf("x=%d 代价=%d 方案数=%d ",x,0,f[x][0]); 27 return; 28 } 29 for(int i=0;i<son[x].size();i++){ 30 dfs(son[x][i]); 31 dep[x]=max(dep[x],dep[son[x][i]]+1); 32 } 33 memset(g,0,sizeof(g)); 34 for(int i=1;i<=dep[son[x][0]]+1;i++){ 35 g[0][0][i]=f[son[x][0]][i-1]; 36 g[0][1][i]=f[son[x][0]][i]; 37 //printf("g[%d][%d][%d]=%d g[%d][%d][%d]=%d ",0,0,i,g[0][0][i],0,1,i,g[0][1][i]); 38 } 39 g[0][1][0]=f[son[x][0]][0]; 40 int cur=0,upw=dep[son[x][0]]+1; 41 for(int i=1;i<son[x].size();i++){ 42 memset(g[cur^1],0,sizeof(g[cur^1])); 43 for(int j=0;j<=upw;j++){ 44 for(int k=0;k<=dep[son[x][i]];k++){ 45 (g[cur^1][0][max(j,k+1)]+=g[cur][0][j]*f[son[x][i]][k]%mod)%=mod; 46 (g[cur^1][1][max(j,k+1)]+=g[cur][1][j]*f[son[x][i]][k]%mod)%=mod; 47 (g[cur^1][1][max(j,k)]+=g[cur][0][j]*f[son[x][i]][k]%mod)%=mod; 48 } 49 } 50 upw=max(dep[son[x][i]]+1,upw); 51 cur^=1; 52 } 53 memcpy(f[x],g[cur][1],sizeof(f[x])); 54 //for(int i=0;i<=dep[x];i++) printf("x=%d 代价=%d 方案=%d ",x,i,f[x][i]); 55 56 } 57 int main(){ 58 scanf("%d",&n); 59 int x,y; 60 long long num=1; 61 for(int i=1;i<=n;i++){ 62 scanf("%d",&x); 63 for(int j=1;j<=x;j++){ 64 scanf("%d",&y); 65 son[i].push_back(y); 66 indu[y]++; 67 } 68 if(x) (num*=pow(x,mod-2)%mod)%=mod; 69 } 70 for(int i=1;i<=n;i++){ 71 if(indu[i]==0){ 72 root=i; 73 break; 74 } 75 } 76 dfs(root); 77 long long sum=0; 78 for(int i=1;i<=n;i++) sum=(sum+i*f[root][i]%mod)%mod; 79 //cout<<sum<<" "<<num<<endl; 80 printf("%lld ",(sum%mod*num%mod)%mod); 81 }
T3:建造游乐场 高难标记
毒瘤题,码量极短,思维量极高23333333
为了保证考试总结的完整性 我决定借用外力(粘贴题解)


先不粘AC代码了(心虚)
第四次

T1 礼物:
实际上是个及其简单的概率期望
But....我经过一下午的钻研(死皮赖脸缠着学长)(以致学长无法吃鸡)才大致明白了
f[i]=∑f[s]*p[j]+∑p[j]*f[i]+1
因为设f[i]表示买到状态为i到最终状态的期望次数
那么那么f[i]是可以由他的下一个状态转移过来
即所有的f[s].如果按原有的逻辑顺序对于f[i]来说转移到f[s]的概率是显然的
但是因为是倒着推,很显然f[s]就应该累加到f[i]上所以:
正向求概率,反向求期望!

1 #include<cstdio> 2 #include<iostream> 3 #define MAXN 25 4 using namespace std; 5 double p[MAXN],f[1<<22],wp[MAXN]; 6 int w[MAXN]; 7 int main() 8 { 9 int n;long long ans1=0; 10 scanf("%d",&n); 11 int maxk=(1<<n)-1; 12 for(int i=1;i<=n;i++) 13 { 14 scanf("%lf%d",&p[i],&w[i]); 15 ans1+=w[i]; 16 } 17 cout<<ans1<<endl; 18 f[maxk]=0; 19 for(int i=0;i<=maxk;i++) 20 { 21 int state=i; 22 for(int j=1;j<=n;j++) 23 { 24 if((state&(1<<(j-1))))continue; 25 wp[state]+=p[j]; 26 } 27 } 28 for(int i=maxk-1;i>=0;i--) 29 { 30 f[i]=1; 31 for(int j=1;j<=n;j++) 32 { 33 if((i&(1<<(j-1))))continue; 34 f[i]+=(f[i|(1<<(j-1))]*p[j]); 35 } 36 f[i]/=wp[i]; 37 //cout<<i<<' '<<f[i]<<endl; 38 } 39 printf("%.3lf",f[0]); 40 return 0; 41 }
T2:通讯
Tarjan缩点+贪心板子题

1 #include<cstdio> 2 #include<iostream> 3 #include<queue> 4 #include<cstring> 5 #define LL long long 6 #define mem(a) memset(a,0,sizeof(a)) 7 #define MAXN 200005 8 #define LL long long 9 using namespace std; 10 struct node{ 11 LL to[MAXN],head[MAXN],w[MAXN],nxt[MAXN],d[MAXN],low[MAXN],dfn[MAXN],s[MAXN],top,tot,num,out[MAXN],n,m,c[MAXN]; 12 LL To[MAXN],Head[MAXN],W[MAXN],Nxt[MAXN],cnt,Cnt,ans; 13 bool in_s[MAXN]; 14 void clear() 15 { 16 mem(head);mem(Head);cnt=Cnt=ans=tot=top=num=0;mem(in_s);mem(dfn); 17 } 18 void add(LL u,LL v,LL val) 19 { 20 to[++cnt]=v; 21 nxt[cnt]=head[u]; 22 w[cnt]=val; 23 head[u]=cnt; 24 return ; 25 } 26 void Add(LL u,LL v,LL val) 27 { 28 To[++Cnt]=v; 29 Nxt[Cnt]=Head[u]; 30 W[Cnt]=val; 31 Head[u]=Cnt; 32 return ; 33 } 34 void Tarjan(LL x) 35 { 36 dfn[x]=low[x]=++tot; 37 s[++top]=x; 38 in_s[x]=1; 39 for(LL i=head[x];i;i=nxt[i]) 40 { 41 LL y=to[i]; 42 if(!dfn[y]) 43 { 44 Tarjan(y); 45 low[x]=min(low[x],low[y]); 46 } 47 else if(in_s[y]) 48 { 49 low[x]=min(low[x],dfn[y]); 50 } 51 } 52 if(low[x]==dfn[x]) 53 { 54 num++; 55 while(top) 56 { 57 LL p=s[top--]; 58 in_s[p]=0; 59 c[p]=num; 60 if(p==x)break; 61 } 62 } 63 } 64 void toposort() 65 { 66 queue<int>Q; 67 memset(d,0x3f,sizeof(d)); 68 d[c[1]]=0; 69 Q.push(c[1]); 70 while(!Q.empty()) 71 { 72 LL x=Q.front();Q.pop(); 73 for(LL i=Head[x];i;i=Nxt[i]) 74 { 75 LL y=To[i]; 76 out[y]--; 77 if(W[i]<d[y]) 78 { 79 d[y]=W[i]; 80 } 81 if(!out[y])Q.push(y); 82 } 83 } 84 return ; 85 } 86 void Build_new() 87 { 88 for(LL i=1;i<=n;i++) 89 for(LL j=head[i];j;j=nxt[j]) 90 { 91 LL k=to[j]; 92 if(c[i]!=c[k]) 93 { 94 Add(c[i],c[k],w[j]); 95 out[c[k]]++; 96 } 97 } 98 } 99 inline LL Rd() 100 { 101 register LL x=0;char c=getchar(); 102 while(c>'9'||c<'0')c=getchar(); 103 while(c<='9'&&c>='0'){x=x*10+c-'0';c=getchar();} 104 return x; 105 } 106 void work() 107 { 108 while(1) 109 { 110 n=Rd(),m=Rd(); 111 if(n==0&&m==0)return ; 112 clear(); 113 while(m--) 114 { 115 LL a=Rd(),b=Rd(),c=Rd(); 116 a++;b++; 117 add(a,b,c); 118 } 119 Tarjan(1); 120 Build_new(); 121 toposort(); 122 for(LL i=1;i<=num;i++)ans+=d[i]; 123 cout<<ans<<endl; 124 } 125 } 126 }E; 127 int main() 128 { 129 E.work(); 130 return 0; 131 }
T3:奇袭(我不会玩甘宁啊) 高难标记
27分算法:维护前缀和扫描
74分算法:维护最大最小值
AC算法:分治
再次膜拜DeepinC
AC代码:

1 #include<cstdio> 2 #include<cstring> 3 #include<iostream> 4 #define MAXN 50005 5 using namespace std; 6 int ans; 7 int w[MAXN],mi[MAXN],ma[MAXN],t[MAXN*2],n; 8 inline int Rd() 9 { 10 int x=0;char c=getchar(); 11 while(c<'0'||c>'9')c=getchar(); 12 while(c>='0'&&c<='9'){x=x*10+c-48;c=getchar();} 13 return x; 14 } 15 int solve(int l,int r) 16 { 17 if(l==r)return 1; 18 int mid=l+r>>1; 19 int lans=solve(l,mid),rans=solve(mid+1,r); 20 ans=lans+rans; 21 ma[mid]=mi[mid]=w[mid]; 22 ma[mid+1]=mi[mid+1]=w[mid+1]; 23 for(int i=mid-1;i>=l;i--) 24 { 25 ma[i]=max(w[i],ma[i+1]); 26 mi[i]=min(w[i],mi[i+1]); 27 } 28 for(int i=mid+2;i<=r;i++) 29 { 30 ma[i]=max(ma[i-1],w[i]); 31 mi[i]=min(mi[i-1],w[i]); 32 } 33 for(int i=mid;i>=l;i--) 34 { 35 int j=ma[i]-mi[i]+i; 36 if(j>mid&&j<=r&&ma[j]<=ma[i]&&mi[j]>=mi[i])ans++; 37 } 38 for(int i=mid+1;i<=r;i++) 39 { 40 int j=i-ma[i]+mi[i]; 41 if(j<=mid&&j>=l&&ma[j]<=ma[i]&&mi[j]>=mi[i])ans++; 42 } 43 int head,tail; 44 head=tail=mid+1; 45 for(int i=mid;i>=l;i--)// maxn in left && minn in right mi[j]<mi[i] && ma[j] <ma[i] 46 { 47 while(ma[tail]<=ma[i]&&tail<=r){t[tail+mi[tail]]++;tail++;} 48 while(mi[head]>=mi[i]&&head<=r){t[head+mi[head]]--;head++;} 49 if(t[i+ma[i]]>0)ans+=t[i+ma[i]]; 50 } 51 while(head<tail){t[head+mi[head]]--;head++;} 52 while(tail<head){t[tail+mi[tail]]++;tail++;} 53 head=tail=mid; 54 for(int i=mid+1;i<=r;i++) 55 { 56 while(ma[tail]<=ma[i]&&tail>=l){t[tail-mi[tail]+MAXN]++;tail--;} 57 while(mi[head]>=mi[i]&&head>=l){t[head-mi[head]+MAXN]--;head--;} 58 if(t[MAXN+i-ma[i]]>0)ans+=t[MAXN+i-ma[i]]; 59 } 60 while(head>tail){t[head-mi[head]+MAXN]--;head--;} 61 while(tail>head){t[tail-mi[tail]+MAXN]++;tail--;} 62 return ans; 63 } 64 int main() 65 { 66 // freopen("da.in","r",stdin); 67 // freopen("my.out","w",stdout); 68 n=Rd(); 69 for(int i=1;i<=n;i++) 70 { 71 int a=Rd(),b=Rd(); 72 w[a]=b; 73 } 74 printf("%d ",solve(1,n)); 75 return 0; 76 } 77 /* 78 8 79 1 2 80 2 6 81 3 1 82 4 7 83 5 3 84 6 5 85 7 4 86 8 8 87 */
第五次

T1:星际旅行
考试想到正解,没有判连通
AC代码:

1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #include<vector> 5 using namespace std; 6 const long long MAXN=200005; 7 long long n,m,out[MAXN],s[MAXN],t[MAXN],add,addy; 8 long long C[MAXN][3]; 9 long long ans; 10 int f[MAXN],siz[MAXN]; 11 bool vst[MAXN]; 12 inline long long Rd() 13 { 14 register long long x=0; 15 char c=getchar(); 16 while(c>'9'||c<'0')c=getchar(); 17 while(c>='0'&&c<='9'){x=x*10+c-48;c=getchar();} 18 return x; 19 } 20 int Get(int a) 21 { 22 return f[a]==a?a:f[a]=Get(f[a]); 23 } 24 void un_ion(int a,int b) 25 { 26 int fa=Get(a),fb=Get(b); 27 f[fa]=fb; 28 siz[fb]+=siz[fa]; 29 } 30 int main() 31 { 32 // freopen("out.in","r",stdin); 33 // freopen("a.txt","w",stdout); 34 n=Rd();m=Rd(); 35 for(int i=1;i<=n;i++)f[i]=i,siz[i]=1; 36 for(long long i=1;i<=m;i++) 37 { 38 s[i]=Rd();t[i]=Rd(); 39 vst[s[i]]=vst[t[i]]=1; 40 if(Get(s[i])!=Get(t[i]))un_ion(s[i],t[i]); 41 if(s[i]==t[i]){add++;ans+=m-add;} 42 else {out[s[i]]++;out[t[i]]++;addy++;} 43 } 44 int xup=0; 45 for(int i=1;i<=n;i++)if(!vst[i])xup++; 46 for(int i=1;i<=n;i++) 47 if(vst[i]&&siz[Get(i)]!=n-xup){cout<<0<<endl;return 0;} 48 else if(vst[i]) break; 49 C[1][0]=C[1][1]=1; 50 for(long long i=2;i<=m;i++) 51 { 52 C[i][0]=1; 53 for(long long j=1;j<=2;j++) 54 C[i][j]=C[i-1][j-1]+C[i-1][j]; 55 } 56 for(long long i=1;i<=n;i++) 57 ans+=C[out[i]][2]; 58 cout<<ans<<endl; 59 return 0; 60 }
T2:砍树
数论分块。
显然: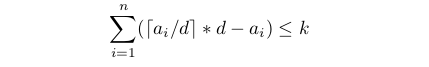
辣么移项后易得:(本博猪没有图,自行脑补)。

1 #include<iostream> 2 #include<cstdio> 3 #include<vector> 4 #include<cmath> 5 #include<algorithm> 6 using namespace std; 7 int n; 8 long long m,a[110],maxn; 9 vector<long long>ok; 10 int judge(long long x){ 11 long long len=0; 12 for(int i=1;i<=n;i++){ 13 int g=ceil((double)a[i]/(double)x); 14 len+=(long long)g; 15 } 16 //cout<<x<<" "<<len<<endl; 17 if(x<=m/len) return 1; 18 return 0; 19 } 20 int main(){ 21 scanf("%d%lld",&n,&m); 22 for(int i=1;i<=n;i++) scanf("%lld",&a[i]),m+=a[i],maxn=max(a[i],maxn); 23 // cout<<"fsdf"<<endl; 24 //maxn=1000000; 25 for(long long i=1;i<=m;i++){ 26 long long sg=0; 27 for(int j=1;j<=n;j++){ 28 sg+=ceil((double)a[j]/(double)i); 29 } 30 //cout<<i<<" "<<sg<<endl; 31 long long sb=m/sg; 32 //cout<<sb<<endl; 33 ok.push_back(sb); 34 i=m/(m/i); 35 } 36 long long ans=0; 37 sort(ok.begin(),ok.end()); 38 for(int i=ok.size()-1;i>=0;i--){ 39 // cout<<ok[i]<<endl; 40 if(judge(ok[i])){ 41 ans=ok[i]; 42 break; 43 } 44 } 45 printf("%lld ",ans); 46 }
T3:超级树
再次借用wd大佬题解
AC代码:

1 #include<cstdio> 2 #include<iostream> 3 #define LL long long 4 #define MAXN 305 5 using namespace std; 6 LL dp[MAXN][MAXN],siz[MAXN]; 7 int main() 8 { 9 LL k,mod; 10 scanf("%lld%lld",&k,&mod); 11 dp[1][1]=dp[1][0]=1; 12 siz[1]=1; 13 for(int i=2;i<=k;i++) 14 { 15 if(siz[i-1]<k)siz[i]=siz[i-1]+siz[i-1]+1; 16 else siz[i]=k+1; 17 for(int l=0;l<=min(k,siz[i-1]);l++) 18 for(int r=0;r<=min(k,siz[i-1]);r++) 19 { 20 if(l+r>k)break; 21 LL num=dp[i-1][l]*dp[i-1][r]%mod; 22 if(!num)continue; 23 dp[i][l+r]+=num;if(dp[i][l+r]>=mod)dp[i][l+r]-=mod; 24 dp[i][l+r+1]+=num;if(dp[i][l+r+1]>=mod)dp[i][l+r+1]-=mod; 25 (dp[i][l+r]+=num*(l+r)*2)%=mod; 26 if(l+r>0) 27 (dp[i][l+r-1]+=num*l*r*2)%=mod; 28 if(l+r>0) 29 (dp[i][l+r-1]+=num*(l*(l-1)+r*(r-1)))%=mod; 30 } 31 } 32 cout<<dp[k][1]%mod<<endl; 33 return 0; 34 }

