在之前的一篇随笔中,通过MATLAB代码实现了ICCP算法中提取等值线和寻找等值线最近点的功能。详情见链接:https://www.cnblogs.com/huangliu1111/p/13089188.html
1、线段集合距离定义
根据1999年的文章《Vehicle localization on gravity maps》,接下来,需要实现ICCP中最重要的步骤,即对等值线最近点构成的线段集合进行刚性变换。刚性变换包括旋转R和平移两个步骤。希望通过刚性变换,使INS指示轨迹线段集合与等值线最近点线段集合的距离最小。
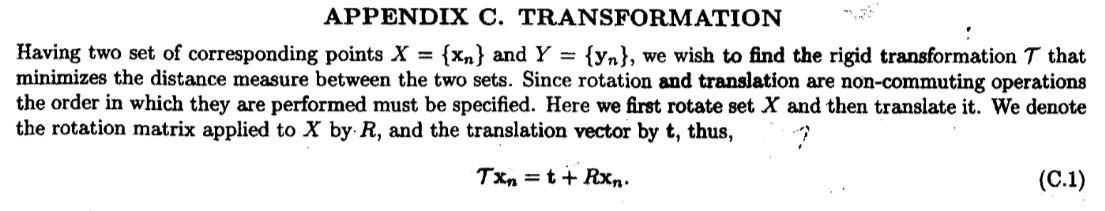

对于线段集合的最近距离描述,该文献直接引用了另一篇1997年的文献《Matching Sets of 3D Line Segments with Application to Polygonal Arc Matching》中的定义。


利用一个线段的中点坐标a、方向向量b和长度l来描述该线段。线段上的所有点均可用这三个参数来表达。两个线段上相对于中点位置相同的点视为一组相关点,所有相关点间的欧式距离之和用于衡量两个线段之间的距离,相当于“相似程度”。
2、旋转矩阵和平移向量
利用旋转矩阵R与线段端点坐标的乘积运算,实现对线段的旋转变换。能够使线段集合距离最小的旋转角度直接通过交叉协方差矩阵S解得(见参考文献《Matching Sets of 3D Line Segments with Application to Polygonal Arc Matching》)。旋转矩阵利用四元数表示。


在线段的计算和变换过程中,主要考虑线段的中点和线段集合的质心。
MATLAB代码如下:
clear all;
yi=[1,-0.5; 3,-1; 5,0];
% 寻找使目标函数最小的变换方式(有权重)
w=0;
w_sum=0;
N=3;
for i=1:N-1
w(i)=((xi(i+1,1)-xi(i,1))^2+(xi(i+1,2)-xi(i,2))^2)^(1/2); %线段长度
x(i,1)=(xi(i+1,1)+xi(i,1))/2;
x(i,2)=(xi(i+1,2)+xi(i,2))/2;
y(i,1)=(yi(i+1,1)+yi(i,1))/2;
y(i,2)=(yi(i+1,2)+yi(i,2))/2;
w_sum=w_sum+w(i); %总长度
end
% 质心
x_center=zeros(1,2);
y_center=zeros(1,2);
for i=1:N-1
x_center(1)=x_center(1)+w(i)*x(i,1);
x_center(2)=x_center(2)+w(i)*x(i,2);
y_center(1)=y_center(1)+w(i)*y(i,1);
y_center(2)=y_center(2)+w(i)*y(i,2);
end
x_center=x_center/w_sum;
y_center=y_center/w_sum;
% 交叉协方差矩阵
S=0;
for i=1:N-1
S=S+w(i)*((y(i,:)-y_center(1,:))'*(x(i,:)-x_center(1,:)));
end
% 求解旋转矩阵
% 最大特征值
lamda(1)=((S(1,1)+S(2,2))^2+(S(1,2)-S(2,1))^2)^(1/2);
lamda(2)=-lamda(1);
lamda(3)=((S(1,1)-S(2,2))^2+(S(1,2)+S(2,1))^2)^(1/2);
lamda(4)=-lamda(3);
lamda_max=max(lamda);
% 旋转矩阵R和平移向量t
R=[cos(theta), -sin(theta);
sin(theta), cos(theta)]; %关于坐标系原点旋转
t=y_center'-R*x_center';
for i=1:N
xis(i,:) = (R*(xi(i,1:2)') +t)';
end
hold on;
plot(yi(:,1),yi(:,2),'*-b');
hold on;
plot(xis(:,1),xis(:,2),'*-g');
hold on;
变换结果如图所示,黑色为原始轨迹(INS轨迹),蓝色为希望靠近的轨迹(等值线最近点轨迹),绿色为进行刚性变换之后的匹配轨迹:
