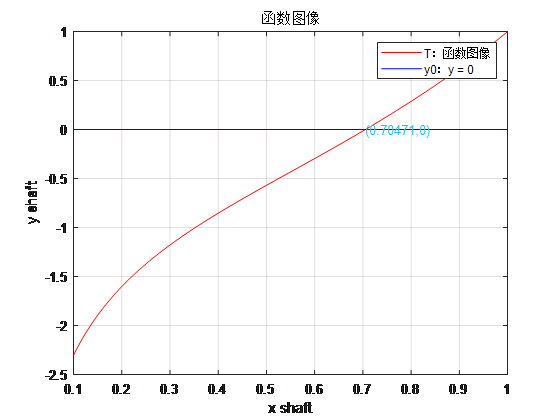
二分法求根主要应用了区间套定理,这一算法实现简单且结果也迭代的较好,但对于复杂函数其结果不理想
1.代码
%%二分法求根
%%f为函数表达式,interval0为初始区间,epsilon为控制精度
function RD = Roots_dichotomy(f,interval0,epsilon)
x_low = interval0(1);x_up = interval0(2);x_ave = (x_low+x_up)/2;
%%作图
t = x_low:(x_up-x_low)/1000:x_up;
T = subs(f,t);
y0 = zeros(1,max(size(t)));
h=figure;
set(h,'color','w');
plot(t,T,'r',t,y0,'b');
grid on
legend('T:函数图像','y0:y = 0');
xlabel('x shaft');ylabel('y shaft');
title('函数图像');
syms x;
%%限定实数解及只在区间中的实数解出现在图象上
X_real = double(solve([f],[0]));
for i = 1:max(size(X_real))
if isreal(X_real(i)) == 1
x_real(i) = X_real(i);
else
x_real(i) =0;
end
end
x_real(x_real==0)=[];
for i = 1:max(size(x_real))
text(x_real(i),0,['(',num2str(x_real(i)),',',num2str(0),')'],'color',[0.02 0.79 0.99]);
end
f_low = subs(f,x_low);f_up = subs(f,x_up);
ub = 100;e=floor(abs(log(epsilon)));
X_up(1) = x_up;X_low(1) = x_low;X_ave(1) = x_ave;
if f_low*f_up > 0
disp('请修改区间!');
interval0 = input('输入区间为:');
RD = Roots_dichotomy(f,interval0,epsilon);
else
%%二分算法
for i = 1:1:ub
f_low = subs(f,x_low);
f_up = subs(f,x_up);
f_ave = subs(f,x_ave);
if f_low*f_ave <0
x_up = x_ave;
x_ave = (x_low+x_up)/2;
elseif f_ave*f_up < 0
x_low = x_ave;
x_ave = (x_low+x_up)/2;
end
delta = x_up -x_low;
X_up(i+1) = x_up;X_low(i+1) = x_low;X_ave(i+1) = x_ave;
if abs(delta) < epsilon
break;
end
end
disp('迭代次数为');
i
disp('输出结果依次是下界迭代值,中值迭代值,上界迭代值');
RD = vpa([X_low;X_ave;X_up],e);
end
end
2.例子
clear all clc syms x; f = x^3+log(x); epsilon=1e-6; interval0 = [0.1,1]; %%二分法 Y = Roots_dichotomy(f,interval0,epsilon)
结果如下
迭代次数为
i =
20
输出结果依次是下界迭代值,中值迭代值,上界迭代值
Y =
[ 0.1, 0.55, 0.55, 0.6625, 0.6625, 0.690625, 0.7046875, 0.7046875, 0.7046875, 0.7046875, 0.7046875, 0.7046875, 0.7046875, 0.7046875, 0.7046875, 0.7046875, 0.7047012329102, 0.7047080993652, 0.7047080993652, 0.7047080993652, 0.7047089576721]
[ 0.55, 0.775, 0.6625, 0.71875, 0.690625, 0.7046875, 0.71171875, 0.708203125, 0.7064453125, 0.70556640625, 0.705126953125, 0.7049072265625, 0.7047973632812, 0.7047424316406, 0.7047149658203, 0.7047012329102, 0.7047080993652, 0.7047115325928, 0.704709815979, 0.7047089576721, 0.7047093868256]
[ 1.0, 1.0, 0.775, 0.775, 0.71875, 0.71875, 0.71875, 0.71171875, 0.708203125, 0.7064453125, 0.70556640625, 0.705126953125, 0.7049072265625, 0.7047973632812, 0.7047424316406, 0.7047149658203, 0.7047149658203, 0.7047149658203, 0.7047115325928, 0.704709815979, 0.704709815979]