【算法与数据结构】二叉树的 后序 遍历

 

非递归后序遍历二叉树相对于先序和中序稍微麻烦一点，网上看到好几种解法，

有一种解法很好，见（http://www.cnblogs.com/dolphin0520/archive/2011/08/25/2153720.html）

 

二叉树

 

 

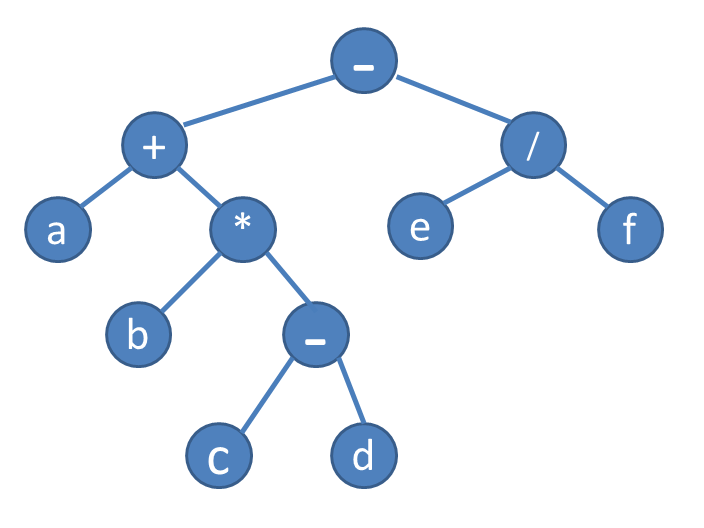
我自己也想到一种解法，不过有个不太好的地方就是每个节点需要借助两个额外的布尔变量来表示该节点的左右子树是否访问(入栈)，

二叉树结构如下

typedef struct _tagBinTree
{
    unsigned char value;
    struct _tagBinTree* left;
    struct _tagBinTree* right;
    bool lbVisited;  //其左子树是否访问过(默认为false，非递归后序遍历用到)
    bool rbVisited;  //其右子树是否访问过(默认为false，非递归后序遍历用到)
}BinTree, *PBinTree;

 

非递归后序遍历二叉树的原理如下

/************************************************************************
非递归后序遍历二叉树原理
首先将根节点入栈
while(栈不空)
{
    取栈顶元素a
    if(a不为NULL)
    {
        if(a左子树没有访问过)
        {
            a左子树入栈，标明a的左子树访问过
        }
        //左子树访问过
        else if(a右子树没有访问过)
        {
            a右子树入栈，表明a的右子树访问过
        }

        //a的左右子树均访问过，访问根节点，然后将a出栈
        else
        {
            Visit(a);
            Pop(a);
        } 
    }

    //栈顶元素为NULL，将其出栈
    else
    {
        Pop(a);        
    } 
}

************************************************************************/

 

 

代码如下

void PostOrderTraverse(PBinTree& pRoot)
{
    stack<PBinTree> stPBinTree;
    stPBinTree.push(pRoot);

    while (! stPBinTree.empty())
    {
        //取栈顶元素
        PBinTree pNode = stPBinTree.top();

        //栈顶元素不为NULL
        if (NULL != pNode)
        {
            //如果其左子树没有访问过
            if (false == pNode->lbVisited)
            {
                //将其左子树入栈，并标明其左子树访问过
                stPBinTree.push(pNode->left);
                pNode->lbVisited = true;
            }

            //如果其右子树没有访问过
            else if (false == pNode->rbVisited)
            {
                //将其右子树入栈，并标明其右子树访问过
                stPBinTree.push(pNode->right);
                pNode->rbVisited = true;
            }

            //其左右子树均已经访问过
            else
            {
                //访问其节点，并将其出栈
                Visit(pNode);
                stPBinTree.pop();
            }
        }

        //栈顶元素为NULL
        else
        {
            //直接将栈顶为NULL的元素出栈
            stPBinTree.pop();
        }         
    }
}

 

 

main函数

cout << "
-----------开始 非递归后序遍历二叉树---------------
";
PostOrderTraverse(pRoot);
cout << "
-----------结束 非递归后序遍历二叉树---------------

";

 

 

执行结果如下