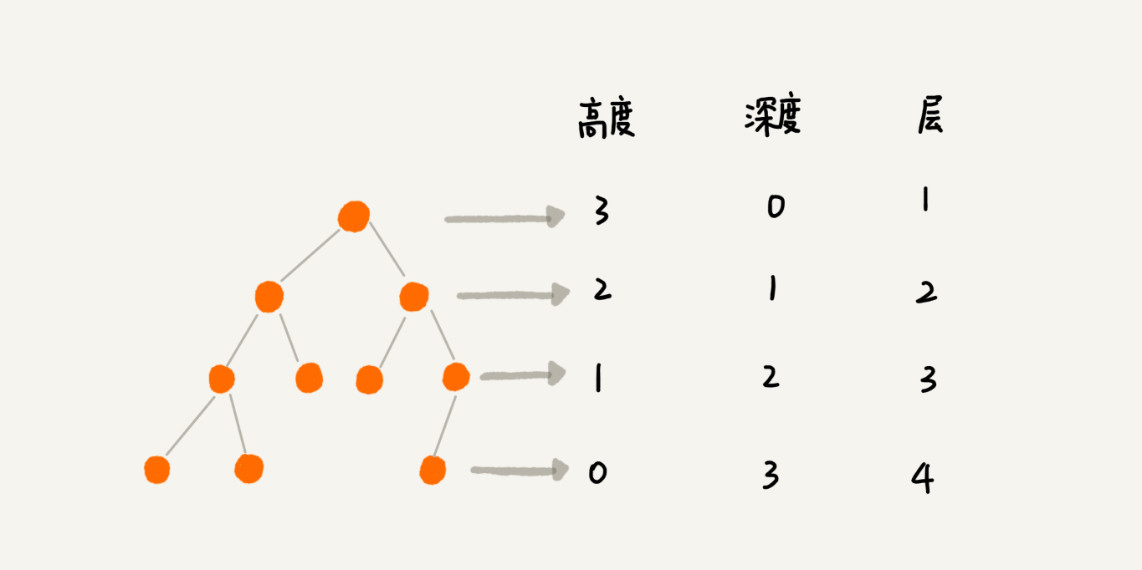
关于二叉树,首先搞清楚“树”,这里面有几个重要的概念:高度(Height)、深度(Depth)、层(Level)。
节点的高度 = 节点到叶子节点的最长路径(边数)
节点的深度 = 根节点到这个节点所经历的边的个数
节点的层数 = 节点的深度 + 1
树的高度 = 根节点的高度
(这张图可以帮助理解一下)
对于二叉树,首先要搞清楚二叉树的概念以及一些特点,这样才能更好的使用二叉树这种数据结构
二叉树:每个节点最多有两个叉,也就是最多有两个子节点,分别是左子节点和右子节点,不过,二叉树并不要求每个节点都有两个子节点,有的节点只有左子节点,有的节点只有右子节点。
满二叉树:叶子节点全部都在最底层,除了叶子节点之外,每个节点都有左右两个子节点
完全二叉树:叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大
一、二叉树的遍历
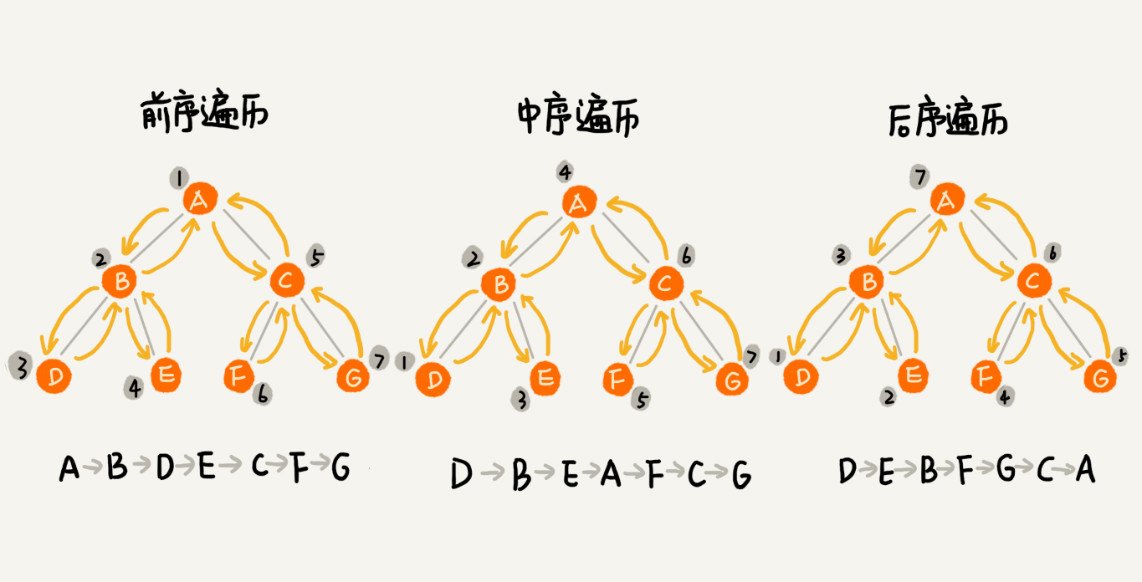
前序遍历:对于树中的任意节点,先打印这个节点本身,再打印它的左子树,最后打印它的右子树
中序遍历:对于树中的任意节点,先打印它的左子树,再打印这个节点本身,最后打印它的右子树
后序遍历:对于树中的任意节点,先打印它的左子树,再打印它的右子树,最后打印这个节点本身
/** * 二叉树(Binary Tree)节点类 * @author ssc * @date 2018.11.16 */ public class BinaryTreeNode { int data; BinaryTreeNode left; BinaryTreeNode right; public BinaryTreeNode(int data){ this.data = data; } } /** * 先序遍历 * 先打印该节点 再打印左子树 然后再打印右子树 * 这三种不同的遍历结构都是一样的,仅仅是先后顺序不一样而已 * * @param node 遍历的节点 */ public void preOrderTraverse(BinaryTreeNode node) { if (node == null){ return; } System.out.print(node.data + " "); preOrderTraverse(node.left); preOrderTraverse(node.right); } /** * 中序遍历 * * 这三种不同的遍历结构都是一样的,仅仅是先后顺序不一样而已 * 先打印左子树 再打印此节点本身 最后打印右子树 * @param node 遍历的节点 */ public void inOrderTraverse(BinaryTreeNode node) { if (node == null){ return; } inOrderTraverse(node.left); System.out.print(node.data + " "); inOrderTraverse(node.right); } /** * 后序遍历 * * 这三种不同的遍历结构都是一样的。仅仅是先后顺序不一样而已 * 先打印左子树 然后再打印右子树 最后打印此节点本身 * @param node 遍历的节点 */ public void postOrderTraverse(BinaryTreeNode node) { if (node == null){ return; } postOrderTraverse(node.left); postOrderTraverse(node.right); System.out.print(node.data + " "); }
二、二叉查找树
二叉查找树:二叉查找树是为了实现快速查找而生的。不过,它不仅仅支持快速查找一个数据,还支持快速插入、删除一个数据
满足二叉查找树的要求:在树中的任意一个节点,其左子树中每个节点的值,都要小于这个节点的值,右子树节点的值大于这个节点的值
1 /** 2 * 二叉树(Binary Tree)节点类 3 * @author ssc 4 * @date 2018.11.16 5 */ 6 public class BinaryTreeNode { 7 8 int data; 9 BinaryTreeNode left; 10 BinaryTreeNode right; 11 12 public BinaryTreeNode(int data){ 13 this.data = data; 14 } 15 16 } 17 18 /** 19 * 二叉查找树(Binary Search Tree) 20 * 21 * 二叉查找树满足的条件:(在树中的任意一个节点,左子树中的每个节点的值都要小于这个节点的值,右子树中每个节点的值都要大于这个节点的值) 22 * @author ssc 23 * @date 2018.11.16 24 */ 25 public class BinarySearchTree { 26 27 private BinaryTreeNode tree; 28 29 /** 30 * 二叉树中的查找操作 31 * @param data 需要查找的数值 32 * @return 33 * 34 */ 35 public BinaryTreeNode find(int data){ 36 BinaryTreeNode p = tree; 37 38 while(p != null){ 39 if(data < p.data){ 40 //查找的数据比根节点小 就在左子树中递归查找 41 p = p.left; 42 }else if(data > p.data){ 43 //查找的数据比根节点大 就在右子树中递归查找 44 p = p.right; 45 }else{ 46 return p; 47 } 48 } 49 return null; 50 } 51 52 /** 53 * 二叉查找树的插入操作 54 * @param data 55 */ 56 public void insert(int data){ 57 if(tree == null){ 58 tree = new BinaryTreeNode(data); 59 return; 60 } 61 62 BinaryTreeNode p = tree; 63 while(p != null){ 64 if(data > p.data){ 65 //插入到右子树 66 if(p.right == null){ 67 p.right = new BinaryTreeNode(data); 68 return; 69 } 70 p = p.right; 71 }else{ 72 //data < p.data 73 //插入到左子树 74 if(p.left == null){ 75 p.left = new BinaryTreeNode(data); 76 return; 77 } 78 p = p.left; 79 } 80 } 81 } 82 83 /** 84 * 二叉查找树 中的删除操作 85 * @param data 86 */ 87 public void delete(int data){ 88 //p指向要删除的节点 初始化指向根节点 89 BinaryTreeNode p = tree; 90 //pp记录的是p的父节点 91 BinaryTreeNode pp = null; 92 93 while(p != null && p.data != data){ 94 pp = p; 95 if(data > p.data){ 96 p = p.right; 97 }else{ 98 p = p.left; 99 } 100 } 101 102 //没有找到 103 if(p == null){ 104 return ; 105 } 106 107 //要删除的节点有两个子节点 108 if(p.right != null && p.left != null){ 109 //查找右子树中的最小节点 110 BinaryTreeNode minP = p.right; 111 //minPP是minP的父节点 112 BinaryTreeNode minPP = p; 113 while(minP.left != null){ 114 minPP = minP; 115 minP = p.left; 116 } 117 //将minP 的数据替换到p 中 118 p.data = minP.data; 119 //删除minP 120 p = minP; 121 pp = minPP; 122 } 123 124 //删除节点是叶子节点 或仅有一个子节点 125 //p 的子节点 126 BinaryTreeNode child; 127 if(p.left != null){ 128 child = p.left; 129 }else if(p.right != null){ 130 child = p.right; 131 }else{ 132 child = null; 133 } 134 135 if(pp == null){ 136 tree = child; 137 }else if(pp.left == p){ 138 pp.left = child; 139 }else{ 140 pp.right = child; 141 } 142 } 143 }
此大部分内容来自极客时间专栏,王争老师的《数据结构与算法之美》