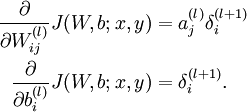原作者:在路上 原文链接:http://zhangliliang.com/2014/09/15/about-caffe-code-full-connected-layer/
今天看全连接层的实现。
主要看的是https://github.com/BVLC/caffe/blob/master/src/caffe/layers/inner_product_layer.cpp
主要是三个方法,setup,forward,backward
- setup 初始化网络参数,包括了w和b
- forward 前向传播的实现
- backward 后向传播的实现
setup
主体的思路,作者的注释给的很清晰。
主要是要弄清楚一些变量对应的含义
1
|
M_ 表示的样本数
|
为了打字方便,以下省略下划线,缩写为M,K,N
forward
实现的功能就是 y=wx+b
1
|
x为输入,维度 MxK
|
具体到代码实现,用的是这个函数caffe_cpu_gemm,具体的函数头为
1
|
void caffe_cpu_gemm<float>(const CBLAS_TRANSPOSE TransA,
|
略长,整理它的功能其实很直观,即C←αA×B+βC
1
|
const CBLAS_TRANSPOSE TransA # A是否转置
|
从实际代码来算,全连接层的forward包括了两步:
1
|
# 这一步表示 y←wx,或者说是y←xw'
|
backward
分成三步:
- 更新w
- 更新b
- 计算delta
一步步来,先来第一步,更新w,对应代码是:
1
|
caffe_cpu_gemm<Dtype>(CblasTrans, CblasNoTrans, N_, K_, M_, (Dtype)1.,
|
对照公式,有
1
|
需要更新的w的梯度的维度是NxK
|
然后是第二步,更新b,对应代码是:
1
|
caffe_cpu_gemv<Dtype>(CblasTrans, M_, N_, (Dtype)1., top_diff,
|
这里用到了caffe_cpu_gemv,简单来说跟上面的caffe_cpu_gemm类似,不过前者是计算矩阵和向量之间的乘法的(从英文命名可以分辨,v for vector, m for matrix)。函数头:
1
|
void caffe_cpu_gemv<float>(const CBLAS_TRANSPOSE TransA, const int M,
|
绕回到具体的代码实现。。如何更新b?根据公式b的梯度直接就是delta
1
|
# 所以对应的代码其实就是将top_diff转置后就可以了(忽略乘上bias_multiplier这步)
|
第三步是计算delta,对应公式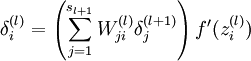
这里面可以忽略掉最后一项f’,因为在caffe实现中,这是由Relu layer来实现的,这里只需要实现括号里面的累加就好了,这个累加其实可以等价于矩阵乘法
1
|
caffe_cpu_gemm<Dtype>(CblasNoTrans, CblasNoTrans, M_, K_, N_, (Dtype)1.,
|