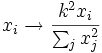A：给你n个数，要求尽可能多的找出匹配，如果两个数匹配，则ai*2 <= aj
排序，从中间切断，分成相等的两半后，对于较大的那一半，从大到小遍历，对于每个数在左边那组找到最大的满足条件的数配对
用一个变量移动一下就好了。这样的配对数量肯定就是最多的。
因为
1：如果左边那一半数量取少一点，比如取a1 a2 a3...ak (k < n/2)
那实际上ak+1 ak+2 .. a n/2 这些数就没啥用了，因为后面那一半数已经足够匹配当前的这些数了，不可能后面还有某些数不匹配而拿这部分数来匹配
2：如果左边那一半数量取大一点，那后边那一部分的数量就小于一半了，这时候最多就只能匹配后面的数的数量了，那还不如把左边多余的那部分去掉呢
所以最优的答案肯定是分在中间的。
B:40*40的01矩阵，很多个询问，问某个子矩形内有多少个全0矩阵
预处理O(n^5),O（1）回答
f[a][b][c][d] = f[a][b][c-1][d] + f[a][b][c][d-1] - f[a][b][c-1][d-1]+sum;
sum是包含右下角那个0的矩形的个数，这个只需要再O(n)扫一遍即可得出
C：给你m<=300个烟花的燃放时间与地点，还有一个价值，燃放的位置是1~n(n <= 150000);,如果烟花燃放的时候人在某个位置，就能
获得 bi - |ai - x|的价值，也就是价值减去位置的绝对值之差，最后问观赏完所有的烟花后最大获得的价值是多大。
dp[i][j]表示前i个时刻停留的j位置的最大价值。然后能够从dp[i-1][k]转移过来，稍微观察
一下就发现k跟j的距离是<=len(len为定长)
然后就用单调队列维护一下定长区间的最大值扫描两遍就好了
D：在一棵树中找一个大小<=k的联通块，使得这个联通块中出现的最长连续的区间最大
不知道那个dfs序的性质这个题还真是难做啊。。
维护two pointers，题目就转换成判断包含LR区间的数的联通块的点的最小个数，可以将
这些数按照dfs序排序后，相邻两个点到lca的距离加起来，然后，第一个点与最后一个点
到lca的距离加起来，这时候发现最小的联通块的每条边都被加了两次，然后就可以求点
数了。
具体实现的时候用一个set维护一下就好了，细节处理的不好会很当疼，不过对于神牛来
说总是有很好的方法可以搞定，看CLJ代码就知道了。。。
E：平面上有n个点，问你有多少个这样的点的集合 (P1, P2), (P3, P4), ..., (P2k - 1, P2k)
- For any two pairs (P2i - 1, P2i) and (P2j - 1, P2j), the circumcircles of triangles OP2i - 1P2j - 1 and OP2iP2j have a single common point, and the circumcircle of triangles OP2i - 1P2j and OP2iP2j - 1 have a single common point.
就是在这个集合里任取两对点，（a , b） （c , d）, 三角形Oac的外接圆与三角形Obd的外接圆有一个公共点，三角形Oab 与三角形Ocd的外接圆有一个公共点
- 反演： http://zh.wikipedia.org/zh-cn/%E5%8F%8D%E6%BC%94
-
反演是种几何变换。给定点O、常数k，点P的变换对应点就是在以O开始的射线OP上的一点 P'使得|OP||OP' | = k2。
反演的结果：
对于点
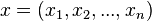，以原点为中心，在直角坐标系的反演变换可写成
-
- 反演中心为O，过O的圆对O的反演就是一条不过O的直线，现在两个圆只相交于O点
-
- ，反演之后的两条直线也应该相交于O点的反演点O*,而O*位于无穷远处，所以两直
-
- 线平行，所以两个圆只有一个交点这件事情就可以转换成a b c d构成一个平行四边形
-
- 。。下面的事情就简单了。反演后对中点哈希即可。
-
