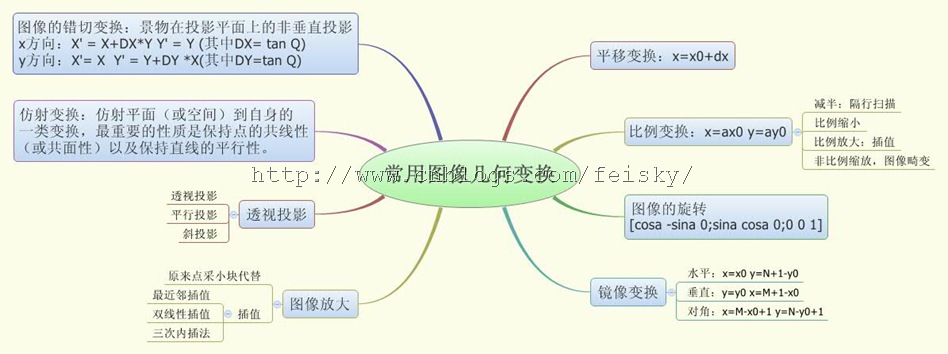
★几何变换不改变像素值,而是改变像素所在的位置。
1.图像的平移
图像的平移非常简单,所用到的是中学学过的直角坐标系的平移变换公式:
x ‘ = x +dx
y’ = y + dy
注:(x,y)为源图像的坐标,(x’,y’)为新图像的坐标,dx对应x的偏移量,dy对应y的偏移量
2.图像的镜像
镜像分为水平镜像和垂直镜像
2.1>水平镜像计算公式如下(图像大小为M*N):
x’ = x
y’ = N-1-y
2.2>垂直镜像计算公式为(图像大小为M*N):
x’ = M-1 –x
y’ = y
3.图像的旋转
图像的旋转计算公式如下:
X’ = X *COS Q – Y *SIN Q Y’ = X *SIN Q + Y*COS Q
•这个计算公式计算出的值为小数,而坐标值为正整数。要用插值处理。
•这个计算公式计算的结果值所在范围与原来的值所在的范围不同。
若以(CX,CY)为中心,角度Q逆时针旋转。
X’ = (X – CX)*COS Q – (Y – YC)*SIN Q + CX
Y’ = (X – CX)*SIN Q + (Y – YC)*COS Q + CY
注:(x,y)为源图像的坐标,(x’,y’)为新图像的坐标
4.图像缩放
n设原图像大小为M*N,缩小为k1M*k2N,(k1<1,k2<1)。算法步骤如下:
n
1)设旧图像是F(i,j), i=1,2,…,M, j=1,2,…,N.
新图像是I(x,y), x=1,2,…,k1M, y=1,2,…,k2N.
2)I(x,y)=F(c1*i,c2*j)
c1=1/k1 c2=1/k2
•这个计算公式计算出的值为小数,而坐标值为正整数。要用插值处理。
5.图像错切
图像的错切变换实际上是平面景物在投影平面上的非垂直投影效果。
n错切的计算公式如下:
5.1 x方向错切
X' = X + DX *Y Y' = Y (其中DX = tan Q)
5.2 y方向错切
X' = X Y' = Y + DY *X (其中DY = tan Q)
注:当在进行图象几何变换时,一般来说图象像数对应的而坐标值为正整数,在几何变换时,若出现了小数,就要进行插值处理。在这里解释线性插值处理。
实践已证明,插值算法对于缩放比例较小的情况是完全可以接受的,令人信服的。一般的,缩小0.5倍以上或放大3.0倍以下,对任何图像都是可以接受的。
最邻近插值(近邻取样法):
最临近插值的的思想很简单。对于通过反向变换得到的的一个浮点坐标,对其进行简单的取整,得到一个整数型坐标,这个整数型坐标对应的像素值就是目的像素的像素值,也就是说,取浮点坐标最邻近的左上角点(对于DIB是右上角,因为它的扫描行是逆序存储的)对应的像素值。可见,最邻近插值简单且直观,但得到的图像质量不高
双线性内插值:
对于一个目的像素,设置坐标通过反向变换得到的浮点坐标为(i+u,j+v),其中i、j均为非负整数,u、v为[0,1]区间的浮点数,则这个像素得值 f(i+u,j+v) 可由原图像中坐标为 (i,j)、(i+1,j)、(i,j+1)、(i+1,j+1)所对应的周围四个像素的值决定,即:
f(i+u,j+v) = (1-u)(1-v)f(i,j) + (1-u)vf(i,j+1) + u(1-v)f(i+1,j) + uvf(i+1,j+1)
其中f(i,j)表示源图像(i,j)处的的像素值,以此类推。
这就是双线性内插值法。双线性内插值法计算量大,但缩放后图像质量高,不会出现像素值不连续的的情况。由于双线性插值具有低通滤波器的性质,使高频分量受损,所以可能会使图像轮廓在一定程度上变得模糊。
三次卷积法能够克服以上两种算法的不足,计算精度高,但计算亮大,他考虑一个浮点坐标(i+u,j+v)周围的16个邻点,目的像素值f(i+u,j+v)可由如下插值公式得到:
f(i+u,j+v) = [A] * [B] * [C]
[A]=[ S(u + 1) S(u + 0) S(u - 1) S(u - 2) ]
┏ f(i-1, j-1) f(i-1, j+0) f(i-1, j+1) f(i-1, j+2) ┓
[B]=┃ f(i+0, j-1) f(i+0, j+0) f(i+0, j+1) f(i+0, j+2) ┃
┃ f(i+1, j-1) f(i+1, j+0) f(i+1, j+1) f(i+1, j+2) ┃
┗ f(i+2, j-1) f(i+2, j+0) f(i+2, j+1) f(i+2, j+2) ┛
┏ S(v + 1) ┓
[C]=┃ S(v + 0) ┃
┃ S(v - 1) ┃
┗ S(v - 2) ┛
┏ 1-2*Abs(x)^2+Abs(x)^3 , 0<=Abs(x)<1
S(x)={ 4-8*Abs(x)+5*Abs(x)^2-Abs(x)^3 , 1<=Abs(x)<2
┗ 0 , Abs(x)>=2
S(x)是对 Sin(x*Pi)/x 的逼近(Pi是圆周率——π)
最邻近插值(近邻取样法)、双线性内插值、三次卷积法 等插值算法对于旋转变换、错切变换、一般线性变换 和 非线性变换 都适用。
//灰度图象旋转,以CX,CY为中心点,Angle为旋转角度。 其中用到了图象旋转,双线性内插值算法。 void GrayImageRotate(LPBYTES,LPBYTED,intCx,intCy,doubleAngle) { double vcos,vsin; double cx,cy,vx,vy,cntx,cnty; int off,off1,off2; int i,j,m,n; double an,svx,svy; double dx0,dy0,dx1,dy1,zz; an = Angle*3.14159/180.0; vcos = cos(an); vsin = sin(an); cntx = (double)Cx; cnty = (double)Cy; cx = -cntx; cy = -cnty; svx = cx*vcos-cy*vsin+cntx; svy = cx*vsin+cy*vcos+cnty; off=0; for(i=0;i<ImageHeight;i++) { vx = svx; vy = svy; for(j=0;j<ImageWidth;j++) { m = (int)vx; n = (int)vy; if((m<1)||(m>ImageWidth-2)||(n<1)||(n>ImageHeight-2)) { D[off]=255;} else { dx0 = vx-m; dy0 = vy-n; dx1 = 1-dx0;dy1 = 1-dy0; off1 = n*ImageWidth+m; zz = 0; zz = S[off1]*dx1*dy1; off2 = off1+1; zz += S[off2]*dx0*dy1; off2 = off1+ImageWidth; zz += S[off2]*dx1*dy0; off2 = off1+ImageWidth+1; zz += S[off2]*dx0*dy0; if(zz>255) zz= 255; if(zz<0) zz = fabs(zz); D[off]=(int)zz; } off++; vx = vx +vcos; vy = vy+vsin; } svx=svx-vsin;svy=svy+vcos; } } /* 函数名称: ImageRotate1 参数: S 原图象 D 旋转后的目标图象 fAngle 图象的旋转角度 说明: 用邻近点插值算法旋转图象 */ void ImageRotate1(LPBYTES,LPBYTED,doublefAngle) { inti,j; doublex,y,x0,y0,dx,dy,xc,yc; xc=double(ImageWidth/2); yc=double(ImageHeight/2); x0=100000.0; y0=0.0; //计算图象的偏移量 GetRotateCoor(x0,y0,xc,yc,fAngle); dx=xc-ImageWidth/2; dy=yc-ImageHeight/2; //新图象从旧图象中取点 for(i=0;i<ImageHeight;i++) { for(j=0;j<ImageWidth;j++) { //由新图象中的坐标得到原图象的坐标 x=j;y=i; x=x+dx; y=y+dy; GetRotateCoor(x0,y0,x,y,-fAngle); //如果原来的点在图象外面直接给一个空值 if(x<0||x>ImageWidth-1||y<0||y>ImageHeight-1) D[j+i*ImageWidth]=0; else D[j+i*ImageWidth]=S[int(x)+int(y)*ImageWidth]; } } } /* 函数名称: GetRotateCoor 参数: x0,y0 基点 x,y 返回后的目标点 fAngle 旋转角度 说明: 计算以基点为中心将目标点旋转一定角度后的坐标 */ void GetRotateCoor(doublex0,doubley0,double& x,double& y,doublefAngle) { doublef,fR; fR=sqrt((x0-x)*(x0-x)+(y0-y)*(y0-y)); f = GetAngle(x0,y0,x,y); f+=fAngle; x=x0+fR*cos(f); y=y0+fR*sin(f); } /* 函数名称: g_Iden_GetAngle 参数: x0,y0 基点 x1,y1 目标点 说明: 计算由基点到目标点的弧度 */ double GetAngle(doublex0,doubley0,doublex1,doubley1) { doublefAngle; if(x1!=x0) fAngle=atan((float)(y1-y0)/(x1-x0)); else if(y1>y0) return 1.570796325; elsereturn 4.712388975; if(x1-x0<0) fAngle=fAngle+3.14159265; if(x1-x0>0&&y1-y0<0) fAngle=fAngle+6.2831853; returnfAngle; }
参考:http://blog.csdn.net/shizhip/archive/2008/04/15/2294833.aspx