朴素贝叶斯扩展

多项式贝叶斯

文本分类

当新来一个文本时，我要对每一个类别y都计算一个向量θy= （θy1，…，θyn） 其中，n表示词汇表中词的种类数，即特征空间的维度

θyi：这个样本如果属于类别 y时，特征 i出现的概率P(xi| y)，即条件概率

分子：这个新文本中特征 i在类别 y下出现的次数

分母：对分子求和

•在机器学习中，朴素贝叶斯分类器是一系列以假设特征之间强独立（朴素）下运用贝叶斯定理为基础的简单概率分类器。

•高度可扩展的，求解过程只需花费线性时间

•目前来说，朴素贝叶斯在文本分类（textclassification）的领域的应用多，无论是sklearn还是Spark Mllib中，都只定制化地实现了在文本分类领域的算法

回忆上面的知识后，看下面的案例：

调用sklearn接口

import pandas as pd
df = pd.DataFrame([[0,1],[1,1],[2,1],[3,-1],[4,-1],
                   [5,-1],[6,1],[7,1],[8,1],[9,-1]])
X = df[[0]]
Y = df[1]
from sklearn.naive_bayes import MultinomialNB
from sklearn.tree import DecisionTreeClassifier
model = MultinomialNB()
model.fit(X,Y)
print(Y.values.T)
model.predict(X)

打印结果：
['beijing', 'chinese', 'japan', 'macao', 'shanghai', 'tokyo']
[[1 2 0 0 0 0]
 [0 2 0 0 1 0]
 [0 1 0 1 0 0]
 [0 1 1 0 0 1]]
[1]

自己实现：

import pandas as pd
import numpy as np
from sklearn.feature_extraction.text import CountVectorizer
df = pd.read_csv("input/bayes_xinxi.txt")  #读取数据
tfCoder =CountVectorizer(token_pattern="[a-zA-Z|u4e00-u9fa5]+")  #TF模型
#训练TF模型
tfCoder.fit(df['words'])
names_feature = tfCoder.get_feature_names()#获取词语名
print(names_feature)
Y =  df['Y'].value_counts().keys()#获取类别种类的list
class_prior = []  #用于存储先验概率
feature_prob = [] #用于存储条件概率
for y in Y: #遍历每个类别
    df2 = df[df['Y']==y]#获取每个类别下的DF
    prior = len(df2)/len(df)#计算先验概率
    #将先验概率加入集合
    class_prior.append(prior)
    #计算条件概率
    a = tfCoder.transform(df2['words']).toarray()
    prob = (np.sum(a,axis=0)+1)/(np.sum(a)+len(names_feature))
    feature_prob.append(prob)
    #将条件概率加入集合
print("-----------进行测试-----------")
X = ['Chinese Chinese Chinese Tokyo Japan'] #训练数据
T =   tfCoder.transform(X).toarray()#将训练数据转为array类型
class_prior =np.array(class_prior)
feature_prob = np.array(feature_prob)
c = feature_prob**T
c
sj = []
for i in range(len(c)):
    s=1
    for j in c[i]:
        s*=j
    sj.append(s)
sj = np.array(sj)
​
Y[np.argmax(sj*class_prior)] #输出概率最大的类别

朴素贝叶斯算法推导

特征属性间是独立得，所以得到：

 

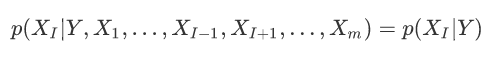
优化一下公式：

 

在给定样本下，p(x1,x2,...,xm)是常数,所以得到:

 

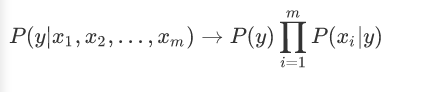
然后求解最大的概率:

 

高斯朴素贝叶斯

Gaussian Naive Bayes是指当特征属性为连续值时，而且分布服从高斯分布，那么在计算P(x|y)的时候可以直接使用高斯分布的概率公式：

 

因此只需要计算出各个类别中此特征项划分的各个均值和标准差

伯努利朴素贝叶斯

Bernoulli Naive Bayes是指当特征属性为连续值时，而且分布服从伯努利分布，那么在计算P(x|y)的时候可以直接使用伯努利分布的概率公式：

 

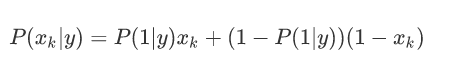
伯努利分布是一种离散分布，只有两种可能的结果。1表示成功，出现的概率为p；0表示失败，出现的概率为q=1-p；其中均值为E(x)=p，方差为Var(X)=p(1-p)

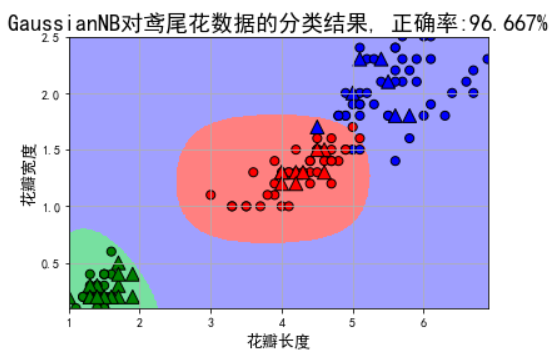
使用高斯朴素贝叶斯实现鸢尾花的分类

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.preprocessing import StandardScaler, MinMaxScaler, PolynomialFeatures
from sklearn.naive_bayes import GaussianNB, MultinomialNB#高斯贝叶斯和多项式朴素贝叶斯
from sklearn.pipeline import Pipeline
from sklearn.metrics import accuracy_score
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
## 设置属性防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
# 花萼长度、花萼宽度，花瓣长度，花瓣宽度
iris_feature_E = 'sepal length', 'sepal width', 'petal length', 'petal width'
iris_feature_C = u'花萼长度', u'花萼宽度', u'花瓣长度', u'花瓣宽度'
iris_class = 'Iris-setosa', 'Iris-versicolor', 'Iris-virginica'
features = [2,3]
## 读取数据
path = './datas/iris.data'  # 数据文件路径
data = pd.read_csv(path, header=None)
x = data[list(range(4))]
x = x[features]
# pd.Categorical().codes  pd.Categorial().codes  pd.Categorical().codes  pd.Categorical().codes
y = pd.Categorical(data[4]).codes ## 直接将数据特征转换为0，1,2
​
print ("总样本数目：%d；特征属性数目：%d" % x.shape)
## 0. 数据分割，形成模型训练数据和测试数据
x_train1, x_test1, y_train1, y_test1 = train_test_split(x, y, train_size=0.8, random_state=14)
x_train, x_test, y_train, y_test = x_train1, x_test1, y_train1, y_test1
print ("训练数据集样本数目：%d, 测试数据集样本数目：%d" % (x_train.shape[0], x_test.shape[0]))
## 高斯贝叶斯模型构建
clf = Pipeline([
        ('sc', StandardScaler()),#标准化，把它转化成了高斯分布
        ('poly', PolynomialFeatures(degree=4)),
        ('clf', GaussianNB())]) # MultinomialNB多项式贝叶斯算法中要求特征属性的取值不能为负数
## 训练模型
clf.fit(x_train, y_train)
## 计算预测值并计算准确率
y_train_hat = clf.predict(x_train)
print ('训练集准确度: %.2f%%' % (100 * accuracy_score(y_train, y_train_hat)))
y_test_hat = clf.predict(x_test)
print ('测试集准确度：%.2f%%' % (100 * accuracy_score(y_test, y_test_hat)))
## 产生区域图
N, M = 500, 500     # 横纵各采样多少个值
x1_min1, x2_min1 = x_train.min()
x1_max1, x2_max1 = x_train.max()
x1_min2, x2_min2 = x_test.min()
x1_max2, x2_max2 = x_test.max()
x1_min = np.min((x1_min1, x1_min2))
x1_max = np.max((x1_max1, x1_max2))
x2_min = np.min((x2_min1, x2_min2))
x2_max = np.max((x2_max1, x2_max2))
​
t1 = np.linspace(x1_min, x1_max, N)
t2 = np.linspace(x2_min, x2_max, N)
x1, x2 = np.meshgrid(t1, t2)  # 生成网格采样点
x_show = np.dstack((x1.flat, x2.flat))[0] # 测试点
​
cm_light = mpl.colors.ListedColormap(['#77E0A0', '#FF8080', '#A0A0FF'])
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
y_show_hat = clf.predict(x_show)                  # 预测值
y_show_hat = y_show_hat.reshape(x1.shape)
## 画图
plt.figure(facecolor='w')
plt.pcolormesh(x1, x2, y_show_hat, cmap=cm_light)     # 预测值的显示
plt.scatter(x_train[features[0]], x_train[features[1]], c=y_train, edgecolors='k', s=50, cmap=cm_dark)
plt.scatter(x_test[features[0]], x_test[features[1]], c=y_test, marker='^', edgecolors='k', s=120, cmap=cm_dark)
plt.xlabel(iris_feature_C[features[0]], fontsize=13)
plt.ylabel(iris_feature_C[features[1]], fontsize=13)
plt.xlim(x1_min, x1_max)
plt.ylim(x2_min, x2_max)
plt.title(u'GaussianNB对鸢尾花数据的分类结果, 正确率:%.3f%%' % (100 * accuracy_score(y_test, y_test_hat)), fontsize=18)
plt.grid(True)
plt.show()

​

使用Ridge KNN 多项式朴素贝叶斯 伯努利朴素贝叶斯 随机森林

SVM LinearSVC-11 LinearSVC-l2

import numpy as np
from time import time
import matplotlib.pyplot as plt
import matplotlib as mpl
​
from sklearn.datasets import fetch_20newsgroups#引入新闻数据包
​
from sklearn.feature_extraction.text import TfidfVectorizer#做tfidf编码
​
from sklearn.feature_selection import SelectKBest, chi2#卡方检验——特征筛选
from sklearn.linear_model import RidgeClassifier
from sklearn.svm import LinearSVC,SVC
from sklearn.naive_bayes import MultinomialNB, BernoulliNB #引入多项式和伯努利的贝叶斯
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV
from sklearn import metrics
###  基准模型方法
def benchmark(clf,name):
    print (u'分类器：', clf)
    
    ##  设置最优参数，并使用5折交叉验证获取最优参数值
    alpha_can = np.logspace(-2, 1, 10)
    model = GridSearchCV(clf, param_grid={'alpha': alpha_can}, cv=5)
    m = alpha_can.size
    
    ## 如果模型有一个参数是alpha，进行设置
    if hasattr(clf, 'alpha'):
        model.set_params(param_grid={'alpha': alpha_can})
        m = alpha_can.size
    ## 如果模型有一个k近邻的参数，进行设置
    if hasattr(clf, 'n_neighbors'):
        neighbors_can = np.arange(1, 15)
        model.set_params(param_grid={'n_neighbors': neighbors_can})
        m = neighbors_can.size
    ## LinearSVC最优参数配置
    if hasattr(clf, 'C'):
        C_can = np.logspace(1, 3, 3)
        model.set_params(param_grid={'C':C_can})
        m = C_can.size
    ## SVM最优参数设置
    if hasattr(clf, 'C') & hasattr(clf, 'gamma'):
        C_can = np.logspace(1, 3, 3)
        gamma_can = np.logspace(-3, 0, 3)
        model.set_params(param_grid={'C':C_can, 'gamma':gamma_can})
        m = C_can.size * gamma_can.size
    ## 设置深度相关参数，决策树
    if hasattr(clf, 'max_depth'):
        max_depth_can = np.arange(4, 10)
        model.set_params(param_grid={'max_depth': max_depth_can})
        m = max_depth_can.size
    
    ## 模型训练
    t_start = time()
    model.fit(x_train, y_train)
    t_end = time()
    t_train = (t_end - t_start) / (5*m)
    print (u'5折交叉验证的训练时间为：%.3f秒/(5*%d)=%.3f秒' % ((t_end - t_start), m, t_train))
    print (u'最优超参数为：', model.best_params_)
    
    ## 模型预测
    t_start = time()
    y_hat = model.predict(x_test)
    t_end = time()
    t_test = t_end - t_start
    print (u'测试时间：%.3f秒' % t_test)
    
    ## 模型效果评估
    train_acc = metrics.accuracy_score(y_train, model.predict(x_train))
    test_acc = metrics.accuracy_score(y_test, y_hat)
    print (u'训练集准确率：%.2f%%' % (100 * train_acc))
    print (u'测试集准确率：%.2f%%' % (100 * test_acc))
    
    ## 返回结果(训练时间耗时，预测数据耗时，训练数据错误率，测试数据错误率, 名称)
    return t_train, t_test, 1-train_acc, 1-test_acc, name
    ## 设置属性防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
### 数据加载
print (u'加载数据...')
t_start = time()
## 不要头部信息
remove = ('headers', 'footers', 'quotes')
## 只要这四类数据
categories = 'alt.atheism', 'talk.religion.misc', 'comp.graphics', 'sci.space'
​
## 分别加载训练数据和测试数据
data_train = fetch_20newsgroups(data_home='./datas/',subset='train', categories=categories, shuffle=True, random_state=0, remove=remove)
data_test = fetch_20newsgroups(data_home='./datas/',subset='test', categories=categories, shuffle=True, random_state=0, remove=remove)
​
## 完成
print (u"完成数据加载过程.耗时:%.3fs" % (time() - t_start))
### 获取加载数据的储存空间
def size_mb(docs):
    return sum(len(s.encode('utf-8')) for s in docs) / 1e6
​
categories = data_train.target_names
data_train_size_mb = size_mb(data_train.data)
data_test_size_mb = size_mb(data_test.data)
​
print (u'数据类型：', type(data_train.data))
print("%d文本数量 - %0.3fMB (训练数据集)" % (len(data_train.data), data_train_size_mb))
print("%d文本数量 - %0.3fMB (测试数据集)" % (len(data_test.data), data_test_size_mb))
print (u'训练集和测试集使用的%d个类别的名称：' % len(categories))
print(categories)
### 数据重命名
x_train = data_train.data
y_train = data_train.target
x_test = data_test.data
y_test = data_test.target
### 输出前5个样本
print (u' -- 前5个文本 -- ')
for i in range(5):
    print (u'文本%d(属于类别 - %s)：' % (i+1, categories[y_train[i]]))
    print (x_train[i])
    print ('

')
### 文档转换为向量
## 转换
# 要求输入的数据类型必须是list，list中的每条数据，单词是以空格分割开的
vectorizer = TfidfVectorizer(input='content', stop_words='english', max_df=0.5, sublinear_tf=True)
x_train = vectorizer.fit_transform(data_train.data)  # x_train是稀疏的，scipy.sparse.csr.csr_matrix
x_test = vectorizer.transform(data_test.data)
print (u'训练集样本个数：%d，特征个数：%d' % x_train.shape)
print (u'停止词:
')
print(vectorizer.get_stop_words())
## 获取最终的特征属性名称
feature_names = np.asarray(vectorizer.get_feature_names())
## 特征选择
ch2 = SelectKBest(chi2, k=1000)
x_train = ch2.fit_transform(x_train, y_train)
x_test = ch2.transform(x_test)
feature_names = [feature_names[i] for i in ch2.get_support(indices=True)]
### 使用不同的分类器对数据进行比较
print (u'分类器的比较：
')
clfs = [
    [RidgeClassifier(), 'Ridge'],
    [KNeighborsClassifier(), 'KNN'],
    [MultinomialNB(), 'MultinomialNB'],
    [BernoulliNB(), 'BernoulliNB'],
    [RandomForestClassifier(n_estimators=200), 'RandomForest'],
    [SVC(), 'SVM'],
    [LinearSVC(loss='squared_hinge', penalty='l1', dual=False, tol=1e-4), 'LinearSVC-l1'],
    [LinearSVC(loss='squared_hinge', penalty='l2', dual=False, tol=1e-4), 'LinearSVC-l2']
]
​
## 将训练数据保存到一个列表中
result = []
for clf,name in clfs:
    # 计算算法结果
    a = benchmark(clf,name)
    # 追加到一个列表中，方便进行展示操作
    result.append(a)
    print ('
')
## 将列表转换为数组
result = np.array(result)
### 获取需要画图的数据
result = [[x[i] for x in result] for i in range(5)]
training_time, test_time, training_err, test_err, clf_names = result
​
training_time = np.array(training_time).astype(np.float)
test_time = np.array(test_time).astype(np.float)
training_err = np.array(training_err).astype(np.float)
test_err = np.array(test_err).astype(np.float)
### 画图
x = np.arange(len(training_time))
plt.figure(figsize=(10, 7), facecolor='w')
ax = plt.axes()
b0 = ax.bar(x+0.1, training_err, width=0.2, color='#77E0A0')
b1 = ax.bar(x+0.3, test_err, width=0.2, color='#8800FF')
ax2 = ax.twinx()
b2 = ax2.bar(x+0.5, training_time, width=0.2, color='#FFA0A0')
b3 = ax2.bar(x+0.7, test_time, width=0.2, color='#FF8080')
plt.xticks(x+0.5, clf_names)
plt.legend([b0[0], b1[0], b2[0], b3[0]], (u'训练集错误率', u'测试集错误率', u'训练时间', u'测试时间'), loc='upper left', shadow=True)
plt.title(u'新闻组文本数据分类及不同分类器效果比较', fontsize=18)
plt.xlabel(u'分类器名称')
plt.grid(True)
plt.tight_layout(2)
plt.show()