二叉树的遍历与树的转换
一、 二叉树的遍历:
在程序设计基础第三单元中有这么个关于案情分析的逻辑问题:
某地刑侦大队对涉及6个嫌疑人的一桩疑案进行分析:
- A、B至少有1人作案
- A、E、F 3人中至少有2人参与作案
- A、D不可能是同案犯
- B、C或同时作案,或与本案无关
- C、D中有且仅有1 人作案
- 如果D没有参与作案,则E也不可能参与作案
试分析出作案人员是谁?
这个问题的逻辑我们已经都明白了,但是怎么将其转换成代码写入我们的程序呢?这就需要我们了解二叉树是如何遍历的。
- 1. 什么是二叉树的遍历
对二叉树的遍历,即对二叉树的每个结点都访问,且只访问一次。遍历的目的是运算。有了遍历我们就能够访问每一个结点,对其数据进行计算和处理。
- 2. 二叉树遍历的方法

(1)先序遍历
先序遍历:根节点、左子树、右子树。
先序遍历的序列是:A B D E C。
(2)中序遍历
中序遍历:左子树、根节点、右子树。
中序遍历的序列是:D B E A C。
(3)后序遍历
后序遍历:左子树、右子树、根节点。
后序遍历的序列是:D E B C A。
如本单元开始讲述的罪犯问题,解题思路是
(1) 将案情写成逻辑表达式
将案情描述写成逻辑表达式,从第1条到第6条依次用CC1,CC2,C3,CC4,CC5,CC6来表示。用A,B,C,D,E,F分别来表示6个人的变量,其中6个变量的值也只能是0或者1。则可以推导出
CC1:A和B至少有一人作案。因此有CC1=(A||B);
CC2:A和D不可能是同案犯。因此有CC2=!(A&&D);
CC3:A,E,F中至少有两人涉嫌作案,分析有3种可能,第1种,A和E作案,写成(A&&E);第二种,A和F作案,写成(A&&F);第三种,E和F作案,写成(E&&F)。这三种可能性是或的关系,因此有CC3=(A&&E)||(A&&F)||(E&&F);
CC4:B和C或同时作案,或都与本案无关,分析有2种可能,第1种两人同时作案写成(B&&C),第2种两人都与本案无关写成(!B&&!C),两者为或的关系,因此有CC4= (B&&C)||( !B&&!C)
CC5:C和D中有且仅有一人作案,写成CC5=(C&&!D)||(D&&!C);
CC6:如果D没有参与作案,则E也不可能参与作案。分析得出CC6=D||(!D&&!E);
(2) 破案综合判断条件
将案情分析的6条归纳成一个破案综合判断条件CC.
CC=CC1&&CC2&&CC3&&CC4&&CC5&&CC6 当CC为1时,说明6条的每一条都满足情况,就可以结案了。
(3) 遍历
用A,B,C,D,E,F分别来表示6个人的变量,0表示不是作案人,1表示是作案人,其中6个变量的值也只能是作案与没作案两种可能,所以可以采用二叉树的遍历解决此问题。
参考代码:
/* 遍历二叉树解决罪犯问题 */ #include "stdio.h" void main() { int CC1,CC2,CC3,CC4,CC5,CC6,CC;/*定义7个变量分别表示6句话及总结果*/ int A,B,C,D,E,F; /*定义六个人的情况变量*/ for(A=0;A<=1;A++) /*A的两种可能*/ for(B=0;B<=1;B++) /*B的两种可能*/ for(C=0;C<=1;C++) /*C的两种可能*/ for(D=0;D<=1;D++) /*D的两种可能*/ for(E=0;E<=1;E++) /*E的两种可能*/ for(F=0;F<=1;F++) /*F的两种可能*/ { CC1=(A||B); /*第1句话的逻辑表达式*/ CC2=!(A&&D); /*第2句话的逻辑表达式*/ CC3=(A&&E)||(A&&F)||(E&&F); /*第3句话的逻辑表达式*/ CC4= (B&&C)||(!B&&!C); /*第4句话的逻辑表达式*/ CC5=(C&&!D)||(D&&!C); /*第5句话的逻辑表达式*/ CC6=D||(!D&&!E); /*第6句话的逻辑表达式*/ if((CC=CC1&&CC2&&CC3&&CC4&&CC5&&CC6)==1 ) /*判断条件都成立*/ { /*输出判断结果*/ A==0?printf("A不是罪犯 "):printf("A是犯罪 "); B==0?printf("B不是罪犯 "):printf("B是犯罪 "); C==0?printf("C不是罪犯 "):printf("C是犯罪 "); D==0?printf("D不是罪犯 "):printf("D是犯罪 "); E==0?printf("E不是罪犯 "):printf("E是犯罪 "); F==0?printf("F不是罪犯 "):printf("F是犯罪 "); } } }

一、 树、森林与二叉树的转换:
我们前面已经讲过了树的定义和存储结构,对于树来说,在满足树的条件下可以是任意形状,一个结点可以有任意多个孩子,显然对树的处理要复杂的多,去研究关于树的性质和算法,真的不容易。有没有简单的办法解决对树处理的难题呢?
我们前边也讲了二叉树,尽管它也是树,但由于每个结点最多只能有左孩子和右孩子,面对的变化就少很多了。因此很多性质和算法都被研究了出来。如果所有的树都像二叉树一样方便就好了。
在讲树的存储结构时,我们提到了树的孩子兄弟法可以将一棵树用二叉链表进行存储,所以借助二叉链表,树和二叉树可以相互进行转换。从物理结构来看,它们的二叉链表也是相同的,只是解释不太一样而已。因此,只要我们设定一定的规则,用二叉树来表示树,甚至表示森林都是可以的,森林与二叉树也可以相互进行转换。
- 1. 树转换为二叉树
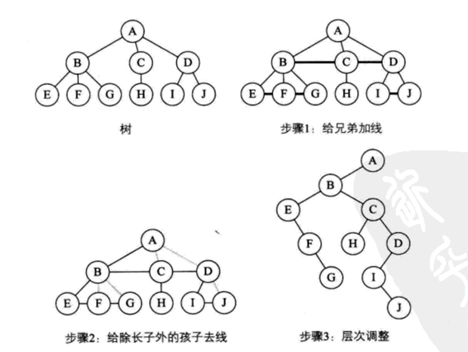
将树转换为二叉树的步骤如下:
(1)加线。在所有 兄弟结点之间加一条连线。
(2)去线。对树中每个结点,只保留它与第一个孩子结点的连线,删除它与其他孩子结点之间的连线。
(3)层次调整。以树的根结点为轴心,为整棵树顺时针旋转一定的角度,使之结构层次分明。注意第一个孩子是二叉树结点的左孩子,兄弟转换过来的孩子是结点的右孩子。
如下图所示,一棵树经过三个步骤转换为一棵二叉树。初学者容易犯的错误是在层次 调整时,弄错了左右孩子的关系。比如图中F、G本都是树的结点B的孩子,是结点E的兄弟,因此转换后,F就是二叉树结点E的右孩子,G是二叉树结点F的右孩子。
- 1. 二叉树转换为树
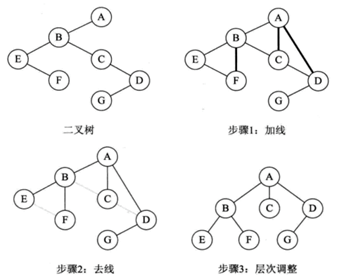
二叉树转换为树是树转换成二叉树的逆过程,也就是反过来做而已。步骤如下:
(1)加线。若某结点的左孩子结点存在,则将这个左孩子的右孩子结点、右孩子的右孩子结点、右孩子的右孩子的右孩子结点······,反正就是左孩子的n个右孩子结点都作为此节点的孩子。将该结点与这些右孩子结点用线连接起来。
(2)去线。删除原二叉树中所有结点与其右孩子结点的连线。
(3)层次调整。使之结构层次分明。
- 1. 二叉树转换为森林
判断一棵二叉树能够转换成一棵树还是森林,标准跟简单,那就是只要看这棵二叉树的根结点有没有叶子,有就是森林,没有就是一棵树。那么如果是转换成森林,步骤如下:
(1)从根结点开始,若右孩子存在,则把与右孩子结点的连线删除,再查看分离后的二叉树,若右孩子存在,则连线删除······,直到所有右孩子连线都删除为止,得到分离的二叉树。
(2)再将每棵树分离后的二叉树转换为树即可。

一、
赫夫曼(Huffman)树,又称最优树,是一类带权路径长度最短的树,有着广泛的应用。本节先讨论最优二叉树。
- 1. 最优二叉树
首先给出路径和路径长度的概念。从树中一个结点到另一个结点之间的分支构成了这两个结点之间的路径。路径上分支的数目称作路径长度。树的路径长度是从树根到每一个结点的路径长度之和。完全二叉树就是这种路径长度最短的二叉树。
若将上述概念推广到一半情况,考虑带权的结点。结点的带权路径路径长度为该结点到树根之间的路径长度与结点上的权的乘积。树的带权路径长度为树中所有叶子结点的带权路径长度之和,通常记作WPL=。
假设有n个权值{},试构造一棵有n个叶子结点的二叉树,每个叶子结点带权为,则其中带权路径长度WPL最小的二叉树称作最优二叉树或赫夫曼树。
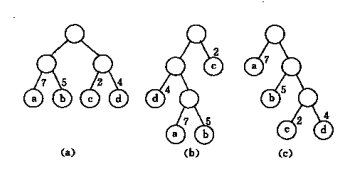
例如,下图中的3棵二叉树,都有4个叶子结点a、b、c、d,分别带权7、5、2、4,它们的带权路径长度分别为
(a) WPL=7×2+5×2+2×2+4×2=36
(b) WPL=7×3+5×3+2×1+4×2=46
(c) WPL=7×1+5×2+2×3+4×3=35
其中以(c)树的为最小。可以验证,它恰为赫夫曼树,即带权路径长度在所有带权为7、5、2、4的四个叶子结点的的二叉树中居最小。
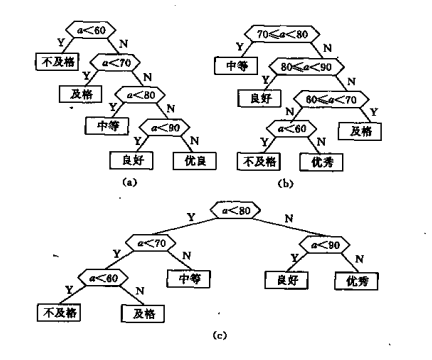
在解某判定问题时,利用赫夫曼树可以得到最佳判定算法。例如,要编制一个将百分之转换为五级分制的程序。显然很简单,只要利用条件语句便可完成。如:
if(a<60)b=”bad”;
else if(a<70) b=”pass”;
else if(a<80) b=”general”;
else if(a<90) b=”good”;
else b=”excellent”;
这个判定过程可以图(a)的判定树表示。如果上述程序需反复使用,而且每次的输入量很大,则考虑上述程序的质量问题,即操作所需要的时间。因为实际生活中学生的成绩在5个等级上分布是不均匀的。假设其分布规律如下表所示:

则80%以上的数据需要进行3次或3次以上的比较才能得出结果。假定以5,15,40,30和10为权构造一棵5个叶子结点的赫夫曼树如图(b)所示的判定过程,它可以使大部分数据经过比较少的比较次数得出结果。但由于每个判定框都有两次比较,将这两次比较分开,我们能得到如图(c)所示的判定树,按此判定树可以写出相应的程序。假设现有10000个输入数据,若按(a)的判定过程进行操作,则总共需要进行31500次比较;而按(c)的判定过程进行操作,则总共仅需进行22000次比较。这样就大大提高程序的效率。
那么如何构造赫夫曼树呢?赫夫曼最早给出一个带有规律的算法,俗称赫夫曼算法。现叙述如下:
(1) n个权值{},将每个结点看成无左右子树的一棵树
(2) 选择权值最小的两个构造一棵新的二叉树,根结点记为这两个权值之和
(3) 删除这两个树,用新得到的二叉树加入进去
(4) 重复(2)和(3),直到只剩一棵树为止。这棵树便是赫夫曼树。
例如下图所示的赫夫曼树构造过程。其中,根结点上标注的数字是所赋的权。
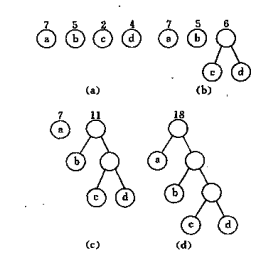
- 1. 赫夫曼编码
电报作为远距离的通信手段,即将需传送的文字转换成由二进制的字符组成的字符串。例如,假设需传送电文为’A B A C C D A’,它只有4种字符,只需要两个字符的串便可分辨。假设A、B、C、D的编码分别为:00、01、10、11,则上述7个字符的电文便为’00010010101100’,总长14位,对方接收时,可按二位一分进行译码。
当然,在传送电文时,希望总长尽可能短。如果对每个字符设计长度不等的编码,且让电文中出现次数较多的字符采用尽可能短的编码,则传送电文的总长便可减少。如果设计A、B、C、D的编码分别为0、00、1、01,则上述7个字符的电文可转换成总长度为9的字符串’000011010’。但是这样的电文无法翻译,例如传送过去的前4个字符子串’0000’就可有多种译法,或是’AAAA’或是’ABA’,也可以是’BB’等。因此,若要设计长度不等的编码,则必须是任一个字符的编码都不是另一个字符编码的前缀,这种编码称做前缀编码。
可以利用二叉树来设计二进制的前缀编码。假设有一颗如图所示的二叉树,其4个叶子结点分别表示为A、B、C、D这四个字符,且约定左分支表示’0’,右分支表示字符’1’,则可以从根结点到叶子结点的路径上分支字符组成的字符串作为该叶子结点字符的编码。可以证明,如此得到的必为二进制前缀编码。如图所得,A、B、C、D的二进制前缀编码分别为0、10、110和111。
又如何得到使电文总长最短的二进制前缀编码呢?假设每种字符在电文中出现的次数为,其编码长度为,电文中只有n种字符,则电文总长为。对应到二叉树上,若置为叶子结点的权,恰为从根结点到叶子的路径长度。由此可见,设计电文总长最短的二进制前缀编码即以n种字符出现的频率作权,设计一棵赫夫曼树的问题,由此得到的二进制前缀编码 ,便称为赫夫曼编码。
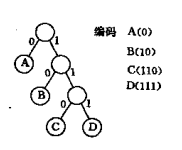
这里进行一下剧透,转到决策树的树结构看一下:
import numpy as np import pandas as pd import matplotlib.pyplot as plt import matplotlib as mpl from sklearn import tree #决策树 from sklearn.tree import DecisionTreeClassifier #分类树 from sklearn.model_selection import train_test_split#测试集和训练集 ## 设置属性防止中文乱码 mpl.rcParams['font.sans-serif'] = [u'SimHei'] mpl.rcParams['axes.unicode_minus'] = False from sklearn.datasets import load_iris iris = load_iris() x = iris.data y = iris.target x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.8, random_state=14) from sklearn.preprocessing import MinMaxScaler #数据归一化 ss = MinMaxScaler () x_train = ss.fit_transform(x_train) x_test = ss.transform(x_test) # entropy 香农熵 model = DecisionTreeClassifier(criterion='entropy',random_state=0, min_samples_split=10) #模型训练 model.fit(x_train, y_train) y_test_hat = model.predict(x_test) # 方式二:直接使用pydotplus插件生成pdf文件 from sklearn import tree import pydotplus dot_data = tree.export_graphviz(model, out_file=None) graph = pydotplus.graph_from_dot_data(dot_data) # graph.write_pdf("iris2.pdf") graph.write_png("decision.png")
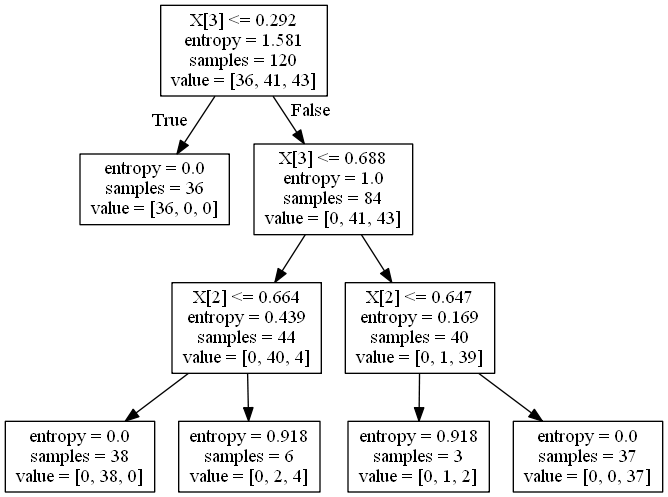
这不很像我们的二叉树嘛,所以二叉树一定要好好学习.