一、 二叉树的定义:
- 1. 为什么要学习二叉树
现在我们来做个游戏,我在纸上已经写好了一个100以内的正整数,请大家想办法猜出我写的是哪一个?注意你们猜的数字不能超过7个,我的回答只会告诉你是“大了”还是“小了”。其实这是一个很经典的折半查找算法。如果我们用下图(下三层省略)的办法,就一定能在7次以内,猜出结果来。
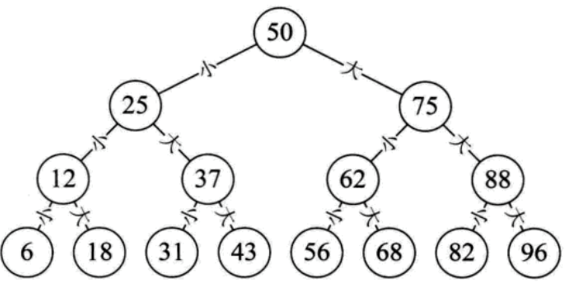
我们发现,如果用这种方式进行查找,效率高的不是一点点。对于这种在某个阶段都是两种结果的情形,比如开和关、0和1、真和假、上和下、对和错、正和反等,都适合用树状结构来建模,而这种树是一种很特殊的树状结构,叫做二叉树。
- 1. 什么是二叉树
二叉树是n(n≥0)个节点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两颗互不相交的、分别称为根结点的左子树和右子树的二叉树组成。
- 2. 二叉树的特点:
(1)每个结点最多有两个子树,所以二叉树中不存在度大于2的结点(注意:不是只有两颗子树,而是最多有。没有子树或者有一颗子树都是可以的)。
(2)左子树和右子树是有顺序的,次序不能任意颠倒。
即使树中某个结点只有一颗子树,也要区分它是左子树还是右子树。如下图所示:树1和树2是同一棵树,但他们却是不同的二叉树。
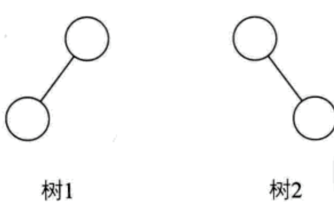
由此,我们可知二叉树的特点是每个节点至多只有二棵子树(即二叉树中不存在大于2的结点), 并且, 二叉树的子树有左右之分, 其次序不能任意颠倒。
二叉树具有五种基本形态:
(1)空二叉树(如图(a)所示)。
(2)只有一个根结点(如图(b)所示)。
(3)根结点只有左子树(如图(c)所示)。
(4)根结点只有右子树(如图(d)所示)。
(5)根结点既有左子树又有右子树(如图(e)所示)。

- 1. 特殊二叉树:
(1)斜树
顾名思义,斜树一定要是斜的,但是往哪斜还是有讲究的。所有的结点都只有左子树的二叉树叫左斜树。所有结点都是只有右子树的二叉树叫右斜树。这两者统称为斜树。斜树的特点:每一层都只有一个结点,结点的个数与二叉树的深度相同。
线性表结构就可以理解为是树的一种极其特殊的表现形式。
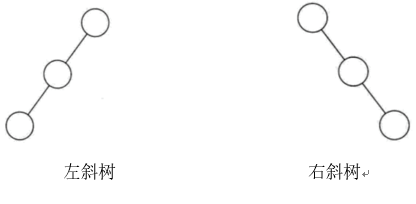
(2)满二叉树
在一棵二叉树中,如果所有的分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。

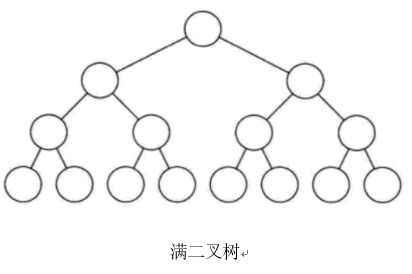
满二叉树的特点有:
1)叶子只能出现在最下一层。出现在其他层就不可能达成平衡。
2)非叶子的结点的度一定是2。
3)在同样深度的二叉树中,满二叉树的结点个数最多,叶子数最多。 叶子数: 2的n-1次方,n为深度
(3)完全二叉树
对一棵具有n个结点的二叉树按层序编号,如果编号为i(1≤i≤n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。
完全二叉树的判定:叶节点只能出现在最下层和次下层,并且最下面一层的结点都集中在该层最左边的若干位置的二叉树。
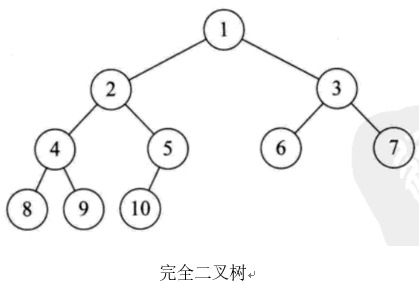
注意:满二叉树一定是一棵完全二叉树,但完全二叉树不一定是满二叉树。
完全二叉树的特点:
1)叶子结点只能出现在最下面两层。
2)最下层的叶子一定集中在左部连续位置。
3)倒数2层,若有叶子结点,一定都在右部连续位置。
4)如果结点度为1,则该节点只有左孩子,即不存在只有右子树的情况。
5)同样结点树的二叉树,完全二叉树的深度最小。
一、 二叉树的性质
- 1. 二叉树的性质1
在二叉树的第i层上至多有2i-1个结点(i≥1)。
- 2. 二叉树的性质2
深度为k的二叉树至多有2k-1个结点(k≥1)
- 3. 二叉树的性质3
对任何一棵二叉树T,如果其终端结点数(即叶子结点数)为n0,度为2的结点数为n2,则n0=n2+1。
- 4. 二叉树的性质4
具有n个结点的完全二叉树的深度为 log2n + 1( x 表示不大于x的最大整数)。
- 5. 二叉树的性质5
如果对一棵有n个结点的完全二叉树(其深度为 log2n + 1)的结点按层序编号(从第一层到第 log2n + 1层,每层从左到右),对任一结点i(1≤i≤n)有:
(1)如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则双亲是结点 i/2 。
(2)如果2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩是结点2i。
(3)如果2i+1>n,则结点i无右孩子;否则其右孩子是结点2i+1。
二、 二叉树的存储结构:
- 1. 二叉树的顺序存储结构
顺序存储对树这种一对多的关系结构实现起来是比较困难的。但是二叉树是一种特殊的树,由于它的特殊性,使得用顺序存储结构也可以实现。
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,比如双亲与孩子的关系,左右兄弟的关系等。
先来看看完全二叉树的顺序存储,一棵完全二叉树如下图所示:
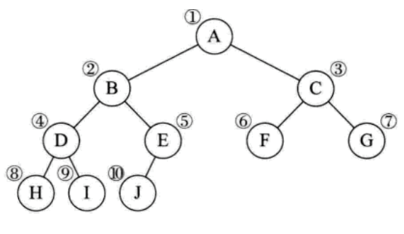
将这棵二叉树存入到数组中,相应的下标对应其同样的位置,如下图所示:

由于完全二叉树定义十分严格,所以用顺序结构也可以表现出二叉树的结构来。
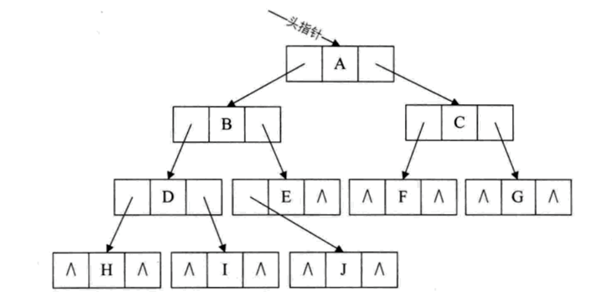
当然,对于一般的二叉树,尽管层序编号不能反映逻辑关系,但是可以将其按完全二叉树编号,只不过,把不存在的结点设置为“^”而已。如下图所示(注意浅色结点表示不存在):
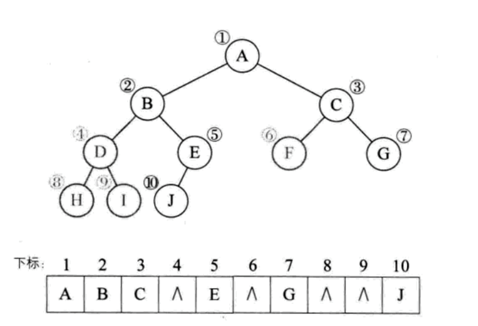
考虑一种比较极端的情况,一棵深度为k的右斜树,它只有k各节点,却需要分配2k-1个存储单元空间,这显然是对存储空间的浪费。如下图所示:
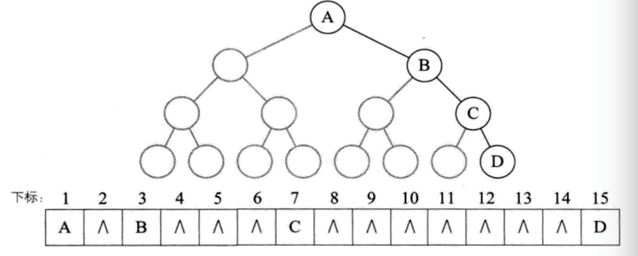
所以,顺序存储结构一般只用于完全二叉树。
- 1. 二叉链表
既然顺序存储结构适用性不强,我们就要考虑链式存储结构。二叉树每个节点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法,我们称这样的链表叫做二叉链表。结点结构图如下表所示:
|
lchild |
data |
rchild |
其中data是数据域,lchild 和rchild 都是指针域,分别存放指向左孩子和右孩子的指针。
以下是二叉链表的结点结构定义代码:
/*二叉树的二叉链表结点结构定义*/ typedef struct BiTNode { TElemType data; struct BiTNode *lchild,*rchild; } BiTNode,*BiTNode
结构示意图如下图所示:
小技巧
如何在c语言中快速的求出数组的长度:
/* Note:Your choice is C IDE */ #include "stdio.h" void main() { int x[11]={15,6,18,3,7,17,20,2,4,13,9}; int len = sizeof(x)/sizeof((x)[0]); printf("%d",len); }
同理在二维数组中:
/* Note:Your choice is C IDE */ #include "stdio.h" void main() { int x[][3] = { 1,2,3,4,5,6 }; int len = sizeof(x)/sizeof((x)[0][0]); printf("%d",len); }
二叉树实现代码
#include<stdio.h> #include<stdlib.h> //二叉查找树结点描述 typedef int KeyType; typedef struct Node { KeyType key; //关键字 struct Node * left; //左孩子指针 struct Node * right; //右孩子指针 struct Node * parent; //指向父节点指针 }Node,*PNode; //往二叉查找树中插入结点 //插入的话,可能要改变根结点的地址,所以传的是二级指针 void inseart(PNode * root,KeyType key) { //初始化插入结点 PNode p=(PNode)malloc(sizeof(Node)); p->key=key; p->left=p->right=p->parent=NULL; //空树时,直接作为根结点 if((*root)==NULL){ *root=p; return; } //插入到当前结点(*root)的左孩子 if((*root)->left == NULL && (*root)->key > key){ p->parent=(*root); (*root)->left=p; return; } //插入到当前结点(*root)的右孩子 if((*root)->right == NULL && (*root)->key < key){ p->parent=(*root); (*root)->right=p; return; } if((*root)->key > key) inseart(&(*root)->left,key); else if((*root)->key < key) inseart(&(*root)->right,key); else return; } //查找元素,找到返回关键字的结点指针,没找到返回NULL PNode search(PNode root,KeyType key) { if(root == NULL) return NULL; if(key > root->key) //查找右子树 return search(root->right,key); else if(key < root->key) //查找左子树 return search(root->left,key); else return root; } //查找最小关键字,空树时返回NULL PNode searchMin(PNode root) { if(root == NULL) return NULL; if(root->left == NULL) return root; else //一直往左孩子找,直到没有左孩子的结点 return searchMin(root->left); } //查找最大关键字,空树时返回NULL PNode searchMax(PNode root) { if(root == NULL) return NULL; if(root->right == NULL) return root; else //一直往右孩子找,直到没有右孩子的结点 return searchMax(root->right); } //查找某个结点的前驱 PNode searchPredecessor(PNode p) { //空树 if(p==NULL) return p; //有左子树、左子树中最大的那个 if(p->left) return searchMax(p->left); //无左子树,查找某个结点的右子树遍历完了 else{ if(p->parent == NULL) return NULL; //向上寻找前驱 while(p){ if(p->parent->right == p) break; p=p->parent; } return p->parent; } } //查找某个结点的后继 PNode searchSuccessor(PNode p) { //空树 if(p==NULL) return p; //有右子树、右子树中最小的那个 if(p->right) return searchMin(p->right); //无右子树,查找某个结点的左子树遍历完了 else{ if(p->parent == NULL) return NULL; //向上寻找后继 while(p){ if(p->parent->left == p) break; p=p->parent; } return p->parent; } } //根据关键字删除某个结点,删除成功返回1,否则返回0 //如果把根结点删掉,那么要改变根结点的地址,所以传二级指针 int deleteNode(PNode* root,KeyType key) { PNode q; //查找到要删除的结点 PNode p=search(*root,key); KeyType temp; //暂存后继结点的值 //没查到此关键字 if(!p) return 0; //1.被删结点是叶子结点,直接删除 if(p->left == NULL && p->right == NULL){ //只有一个元素,删完之后变成一颗空树 if(p->parent == NULL){ free(p); (*root)=NULL; }else{ //删除的结点是父节点的左孩子 if(p->parent->left == p) p->parent->left=NULL; else //删除的结点是父节点的右孩子 p->parent->right=NULL; free(p); } } //2.被删结点只有左子树 else if(p->left && !(p->right)){ p->left->parent=p->parent; //如果删除是父结点,要改变父节点指针 if(p->parent == NULL) *root=p->left; //删除的结点是父节点的左孩子 else if(p->parent->left == p) p->parent->left=p->left; else //删除的结点是父节点的右孩子 p->parent->right=p->left; free(p); } //3.被删结点只有右孩子 else if(p->right && !(p->left)){ p->right->parent=p->parent; //如果删除是父结点,要改变父节点指针 if(p->parent == NULL) *root=p->right; //删除的结点是父节点的左孩子 else if(p->parent->left == p) p->parent->left=p->right; else //删除的结点是父节点的右孩子 p->parent->right=p->right; free(p); } //4.被删除的结点既有左孩子,又有右孩子 //该结点的后继结点肯定无左子树(参考上面查找后继结点函数) //删掉后继结点,后继结点的值代替该结点 else{ //找到要删除结点的后继 q=searchSuccessor(p); temp=q->key; //删除后继结点 deleteNode(root,q->key); p->key=temp; } return 1; } //创建一棵二叉查找树 void create(PNode* root,KeyType *keyArray,int length) { int i; //逐个结点插入二叉树中 for(i=0;i<length;i++) inseart(root,keyArray[i]); } int main(void) { int i; PNode root=NULL; KeyType nodeArray[11]={15,6,18,3,7,17,20,2,4,13,9}; //创建二叉树 create(&root,nodeArray,11); //删除前两个节点 for(i=0;i<2;i++) deleteNode(&root,nodeArray[i]); //查找某个结点的前驱 printf("%d ",searchPredecessor(root)->key); //查找某个结点的后继 printf("%d ",searchSuccessor(root)->key); //查找最小关键字,空树时返回NULL printf("%d ",searchMin(root)->key); //查找最大关键字,空树时返回NULL printf("%d ",searchMax(root)->key); //查找元素,找到返回关键字的结点指针,没找到返回NULL printf("%d ",search(root,13)->key); return 0; }