单调栈

定义：单调栈就是栈内元素单调递增或者单调递减的栈，单调栈只能在栈顶操作。(栈内可以存相应元素的数组下标)

单调栈的维护是 O(n) 级的时间复杂度，因为所有元素只会进入栈一次，并且出栈后再也不会进栈了。

eg：递增栈

　　对于当前元素，如果它的值>栈顶 ： 直接入栈

 　　　　　　　　  如果它的值<栈顶 ： 从栈顶循环pop，直到当前值>栈顶  (找到栈中第一个小于当前值的位置)

性质：

1.单调栈里的元素具有单调性，得到的是当前元素左边小于或大于当前值的有序数列

2.元素加入栈前，会在栈顶端把破坏栈单调性的元素都删除

3.使用单调栈可以找到元素向左遍历第一个比他小的元素，也可以找到元素向左遍历第一个比他大的元素

例题：

Trapping Rain Water

Given [0,1,0,2,1,0,1,3,2,1,2,1], return 6.

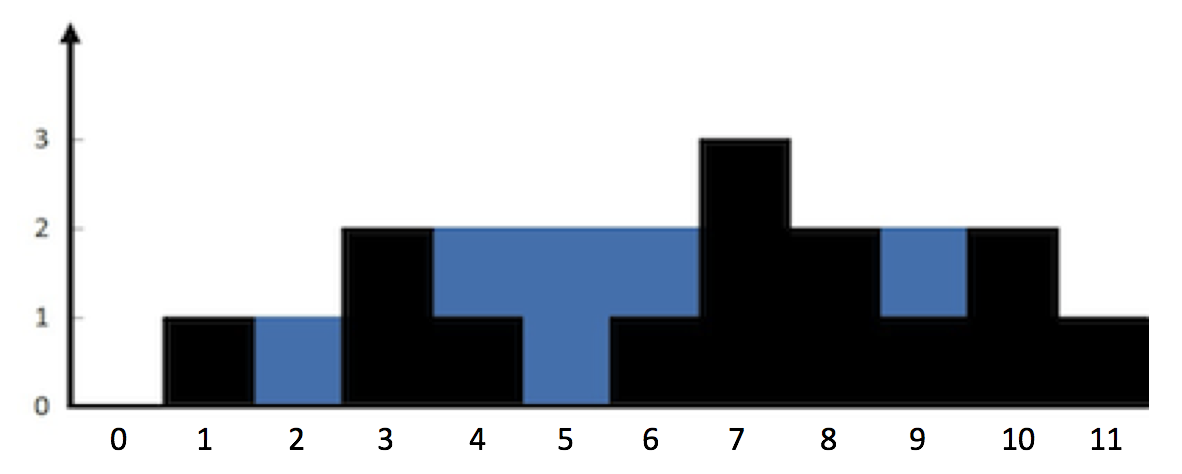
这道题要找一个V字型的水洼才能存住水，高度取两边最大值的minimum

解法一：从左到右过一遍用数组记录，统计当前左侧的最大高度，从右到左过一遍，统计当前右侧的最大高度，再遍历一遍数组统计储水量即可

解法二：双指针，从两边向内遍历，从矮端开始循环统计，更新矮边

解法三：单调栈，维护递减栈，当前高度>栈顶，循环统计，注意必须形成V即栈里至少2个元素，为了统计储水量(长度和高度)栈中存的是下标

Largest Rectangle in Histogram

Given height = [2,1,5,6,2,3],
return 10.

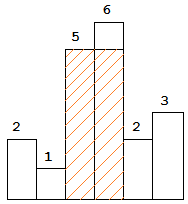
维护递增栈

补0：为了使得最后一块板子也被处理，在高度数组最后面补一个0，这样原先的最后一个板子也可以被处理了

while (i < height.size()) {
    if (st.empty() || height[i] > height[st.top()]) {
        st.push(i++);
    } else {
        int t = st.top(); st.pop();
        if (st.empty())
            res = max(res, height[t] * i);
        else
            res = max(res, height[t] * (i - st.top() - 1));
    }
}

参考:

Adherer