刚体的描述是指刚体上的各类参数。如刚体的物理特征质量、大小，刚体的运动学参数位置、速度、加速度。在描述时，只需要描述位置。刚体的空间状态，即姿态。
为描述刚体的位置可在刚体的质心上固定一个三维坐标系，再选定一个基坐标系，即可描述刚体的空间位置。
刚体坐标系C与基坐标系W-P1其位置本质上是点的位置，在机器人学中用下式表述。
刚体位置的数学描述-P2可以看到，描述刚体在空间中的位置，可以使用三个参数，即一个列向量或列矩阵。
上图P1可以看出，坐标系C相对于坐标系W存在一个空间偏移。该空间偏移由一个位置和一个旋转合成。显然可以通过先将坐标系C旋转一定角度达到与坐标系W平行，再将坐标系C在空间中平移一定距离，就可以将二者重合。可用下式表示
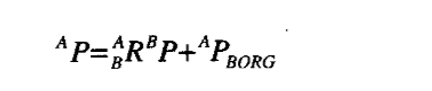
空间中刚体的姿态可由上图P1中的两个坐标系共同描述。坐标系C的三轴单位向量可以投影至坐标系W的三轴单位向量上，将得到九个参数。可用矩阵表示，如下式。
矩阵中的各项为两个单位向量的点乘，即得到单位向量之间夹角的余弦。因此，旋转矩阵又称为方向余弦。
刚体在空间中的位置可以进行平移和旋转，以及两者的复合运算。其中又可以将平移改写为矩阵平移算子，旋转改写为矩阵旋转算子。复合运算可改写为矩阵变换算子。