http://poj.org/problem?id=1191
棋盘分割
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 10776 | Accepted: 3791 |
Description
将一个8*8的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了(n-1)次后,连同最后剩下的矩形棋盘共有n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差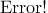 ,其中平均值
,其中平均值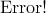 ,xi为第i块矩形棋盘的总分。
,xi为第i块矩形棋盘的总分。
请编程对给出的棋盘及n,求出O'的最小值。

原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割成n块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差
请编程对给出的棋盘及n,求出O'的最小值。
Input
第1行为一个整数n(1 < n < 15)。
第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
第2行至第9行每行为8个小于100的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
Output
仅一个数,为O'(四舍五入精确到小数点后三位)。
Sample Input
3 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 0 3
Sample Output
1.633
思路:
根据题目给出的公式进行化简:
σ=sqrt(((x1-x)^2+(x2-x)^2+...+(xn-x)^2)/n),其中x为x1..xn的平均数.
所以σ^2=((x1-x)^2+(x2-x)^2+...+(xn-x)^2)/n
即n*σ^2=(x1-x)^2+(x2-x)^2+...+(xn-x)^2
=x1^2-2x*x1+x^2+x2^2-2x*x2+x^2+...+xn^2-2x*xn+x^2
=x1^2+x2^2+...+xn^2-2x(x1+x2+...+xn)+n*x^2
=x1^2+x2^2+...+xn^2-2x*n*x+n*x^2
=x1^2+x2^2+...+xn^2-n*x^2
即n*σ^2+n*x^2=x1^2+x2^2+...+xn^2.
n*σ^2+n*x^2中n和x都是一定的,所以只要x1^2+x2^2+...+xn^2最小则σ最小
关于快速计算 左上角为(x1, y1),右下角为(x2, y2)的矩阵的大小:
实现代码:
1 #include<iostream> 2 #include<stdio.h> 3 #include<string.h> 4 #include<math.h> 5 #include<queue> 6 #define SIZE 8 7 #define INF 99999999 8 using namespace std; 9 int map[SIZE+1][SIZE+1]; //存所有矩形 10 int mark[16][SIZE+1][SIZE+1][SIZE+1][SIZE+1]; 11 int sum[SIZE+1][SIZE+1];//sum中每一个位置存放的是左上角为(1,1)点与右下角为当前位置的矩形的所有元素的和,这里下标从1开始 12 13 int min(int a,int b){return a<b?a:b;} 14 15 //计算:左上角为(x1, y1),右下角为(x2, y2)的矩阵平方 16 int powsum(int x1,int y1,int x2,int y2) 17 { 18 int res; 19 res=sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]; 20 return res*res; 21 } 22 23 //深度搜索,计算最小平方和 24 int dfs(int deep,int x1,int y1,int x2,int y2) 25 { 26 if(mark[deep][x1][y1][x2][y2]!=-1) 27 { 28 return mark[deep][x1][y1][x2][y2]; //已经计算过了的避免重复计算,也就是传说中的剪枝 29 } 30 else 31 { 32 if(deep==1||x1==x2||y1==y2) 33 { 34 return mark[deep][x1][y1][x2][y2]=powsum(x1,y1,x2,y2); //当无法再切直接返回 35 } 36 else 37 { 38 int i,maks=INF; //给maks初始化一个足够大的值 39 for(i=x1;i<x2;i++) //横切 40 { 41 maks=min(maks,min(dfs(deep-1,x1,y1,i,y2)+powsum(i+1,y1,x2,y2),dfs(deep-1,i+1,y1,x2,y2)+powsum(x1,y1,i,y2))); 42 } 43 for(i=y1;i<y2;i++) //竖切 44 { 45 maks=min(maks,min(dfs(deep-1,x1,y1,x2,i)+powsum(x1,i+1,x2,y2),dfs(deep-1,x1,i+1,x2,y2)+powsum(x1,y1,x2,i))); 46 } 47 mark[deep][x1][y1][x2][y2]=maks; 48 return maks; 49 } 50 } 51 } 52 53 int main() 54 { 55 int n; 56 while(~scanf("%d",&n)) 57 { 58 int i,j; 59 memset(map,0,sizeof(map)); 60 memset(sum,0,sizeof(sum)); 61 for(i=1;i<=SIZE;i++) 62 { 63 for(j=1;j<=SIZE;j++) 64 { 65 scanf("%d",&map[i][j]); 66 sum[i][j]=sum[i][j-1]+sum[i-1][j]-sum[i-1][j-1]+map[i][j]; // 计算是左上角为(1,1)点与右下角(i,j)的矩形的所有元素的和 67 } 68 } 69 memset(mark,-1,sizeof(mark)); 70 double res=sqrt((double)(dfs(n,1,1,SIZE,SIZE))/n-pow((double)(sum[SIZE][SIZE])/n,2.0)); //展开化简之后的公式 71 printf("%.3lf\n",res); 72 } 73 return 0; 74 }