[MCM] PSO粒子群算法解决TSP问题

%% 该文件演示基于TSP-PSO算法
clc;clear

%% 模拟随机产生数据
x=1:1:100;x=x(:);
y = randi([10,100],100,1);
data=[ones(100,1), x ,y];
cityCoor=[data(:,2) data(:,3)];%城市坐标矩阵,第一维是编号

figure 
plot(cityCoor(:,1),cityCoor(:,2),'ks','LineWidth',1,'MarkerEdgeColor','k','MarkerFaceColor','r')
legend('城市位置')
title('城市分布图','fontsize',12)
xlabel('km','fontsize',12)
ylabel('km','fontsize',12)
%ylim([min(cityCoor(:,2))-1 max(cityCoor(:,2))+1])
for i = 1:size(cityCoor,1)
    text(cityCoor(i,1),cityCoor(i,2),['  ' num2str(i)]);
end
set(gca,'LineWidth',1.5);  %边框加粗,美观
grid on
axis([0 1.1*max(x) 0 1.1*max(y)]); %设置尺寸大小
%% 计算城市间距离
n=size(cityCoor,1);            %城市数目
cityDist=zeros(n,n);           %城市距离矩阵
for i=1:n                      %!!!!!!!!!若城市之间的路线带权,则可将cityDist改为权重
    for j=1:n
        if i~=j
            cityDist(i,j)=((cityCoor(i,1)-cityCoor(j,1))^2+...
                (cityCoor(i,2)-cityCoor(j,2))^2)^0.5;
        end
        cityDist(j,i)=cityDist(i,j);
    end
end

nMax=500;                      %进化次数 迭代次数
indiNumber=1000;               %个体数目  过小陷入局部最优
individual=zeros(indiNumber,n);
%^初始化粒子位置
for i=1:indiNumber
    individual(i,:)=randperm(n);    
end

%% 计算种群适应度
indiFit=fitness(individual,cityCoor,cityDist); %这里cityCoor只需要用到城市的数目,不需要用到坐标
[value,index]=min(indiFit);
tourPbest=individual;                              %当前个体最优
tourGbest=individual(index,:) ;                    %当前全局最优
recordPbest=inf*ones(1,indiNumber);                %个体最优记录
recordGbest=indiFit(index);                        %群体最优记录
xnew1=individual;

%% 循环寻找最优路径
L_best=zeros(1,nMax);
for N=1:nMax
    N %标记迭代次数
    %计算适应度值
    indiFit=fitness(individual,cityCoor,cityDist);
    
    %更新当前最优和历史最优
    for i=1:indiNumber
        if indiFit(i)<recordPbest(i)
            recordPbest(i)=indiFit(i);
            tourPbest(i,:)=individual(i,:);
        end
        if indiFit(i)<recordGbest
            recordGbest=indiFit(i);
            tourGbest=individual(i,:);
        end
    end
    
    [value,index]=min(recordPbest);
    recordGbest(N)=recordPbest(index);
    
    %% 交叉操作
    for i=1:indiNumber
       % 与个体最优进行交叉
        c1=unidrnd(n-1); %产生交叉位
        c2=unidrnd(n-1); %产生交叉位
        while c1==c2
            c1=round(rand*(n-2))+1;
            c2=round(rand*(n-2))+1;
        end
        chb1=min(c1,c2);
        chb2=max(c1,c2);
        cros=tourPbest(i,chb1:chb2);
        ncros=size(cros,2);      
        %删除与交叉区域相同元素
        for j=1:ncros
            for k=1:n
                if xnew1(i,k)==cros(j)
                    xnew1(i,k)=0;
                    for t=1:n-k
                        temp=xnew1(i,k+t-1);
                        xnew1(i,k+t-1)=xnew1(i,k+t);
                        xnew1(i,k+t)=temp;
                    end
                end
            end
        end
        %插入交叉区域
        xnew1(i,n-ncros+1:n)=cros;
        %新路径长度变短则接受
        dist=0;
        for j=1:n-1
            dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
        end
        dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
        if indiFit(i)>dist
            individual(i,:)=xnew1(i,:);
        end
        
        % 与全体最优进行交叉
        c1=round(rand*(n-2))+1;  %产生交叉位
        c2=round(rand*(n-2))+1;  %产生交叉位
        while c1==c2
            c1=round(rand*(n-2))+1;
            c2=round(rand*(n-2))+1;
        end
        chb1=min(c1,c2);
        chb2=max(c1,c2);
        cros=tourGbest(chb1:chb2); 
        ncros=size(cros,2);      
        %删除与交叉区域相同元素
        for j=1:ncros
            for k=1:n
                if xnew1(i,k)==cros(j)
                    xnew1(i,k)=0;
                    for t=1:n-k
                        temp=xnew1(i,k+t-1);
                        xnew1(i,k+t-1)=xnew1(i,k+t);
                        xnew1(i,k+t)=temp;
                    end
                end
            end
        end
        %插入交叉区域
        xnew1(i,n-ncros+1:n)=cros;
        %新路径长度变短则接受
        dist=0;
        for j=1:n-1
            dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
        end
        dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
        if indiFit(i)>dist
            individual(i,:)=xnew1(i,:);
        end
        
       %% 变异操作
        c1=round(rand*(n-1))+1;   %产生变异位
        c2=round(rand*(n-1))+1;   %产生变异位
        while c1==c2
            c1=round(rand*(n-2))+1;
            c2=round(rand*(n-2))+1;
        end
        temp=xnew1(i,c1);
        xnew1(i,c1)=xnew1(i,c2);
        xnew1(i,c2)=temp;
        
        %新路径长度变短则接受
        dist=0;
        for j=1:n-1
            dist=dist+cityDist(xnew1(i,j),xnew1(i,j+1));
        end
        dist=dist+cityDist(xnew1(i,1),xnew1(i,n));
        if indiFit(i)>dist
            individual(i,:)=xnew1(i,:);
        end
    end

    [value,index]=min(indiFit);
    L_best(N)=indiFit(index);
    tourGbest=individual(index,:); 
    
end

%% 结果作图
figure
plot(L_best)
title('算法训练过程')
xlabel('迭代次数')
ylabel('适应度值')
legend('最短距离')
set(gca,'LineWidth',1.5);  %边框加粗,美观
grid on


figure

hold on
plot([cityCoor(tourGbest(1),1),cityCoor(tourGbest(n),1)],[cityCoor(tourGbest(1),2),...
    cityCoor(tourGbest(n),2)],'ks-','Markersize',8,'LineWidth',1,'MarkerEdgeColor','k','MarkerFaceColor','r')
text(cityCoor(1,1),cityCoor(1,2),['  ' num2str(i)]);
hold on
for i=2:n
    plot([cityCoor(tourGbest(i-1),1),cityCoor(tourGbest(i),1)],[cityCoor(tourGbest(i-1),2),...
        cityCoor(tourGbest(i),2)],'ks-','Markersize',8,'LineWidth',1,'MarkerEdgeColor','k','MarkerFaceColor','r')
    text(cityCoor(i,1),cityCoor(i,2),['  ' num2str(i)]);
    hold on
end
legend('规划路径')
title('规划路径','fontsize',10)
xlabel('km','fontsize',10)
ylabel('km','fontsize',10)

grid on
disp(['最短距离:' num2str(L_best(:,nMax))]);
disp(['最短路径:' num2str( [tourGbest tourGbest (1)] )]);
startx=x(tourGbest (1)); %起点x坐标
starty=y(tourGbest (1)); %起点y坐标
endx=x(tourGbest (n));
endy=y(tourGbest (n));
text(startx,starty,'    起点'); %标记起点
text(endx,endy,'    终点')%标记终点
set(gca,'LineWidth',1.5);  %边框加粗,美观
axis([0 1.1*max(x) 0 1.1*max(y)]); %设置尺寸大小

function indiFit=fitness(x,cityCoor,cityDist)
%% 该函数用于计算个体适应度值
%x           input     个体
%cityCoor    input     城市坐标
%cityDist    input     城市距离
%indiFit     output    个体适应度值 

m=size(x,1);
n=size(cityCoor,1);
indiFit=zeros(m,1);
for i=1:m
    for j=1:n-1
        indiFit(i)=indiFit(i)+cityDist(x(i,j),x(i,j+1));
    end
    indiFit(i)=indiFit(i)+cityDist(x(i,1),x(i,n));
end

function dist=dist(x,D)
n=size(x,2);
dist=0;
for i=1:n-1
    dist=dist+D(x(i),x(i+1));
end
dist=dist+D(x(1),x(n));
%测算距离

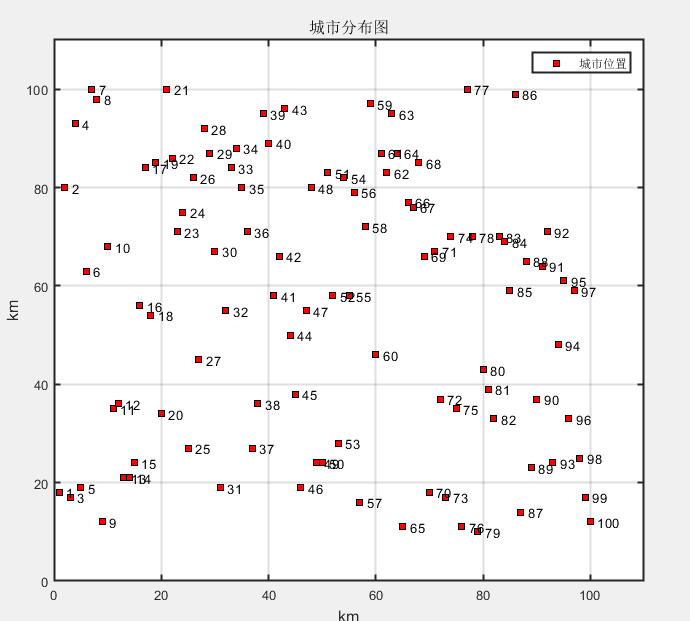
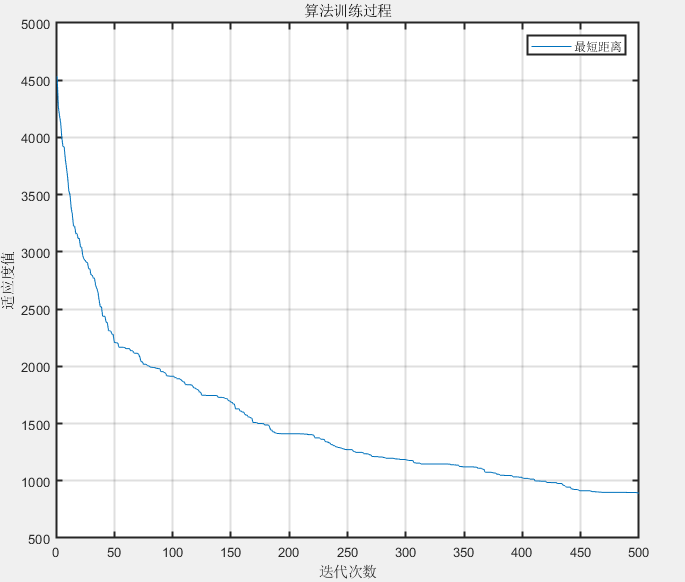
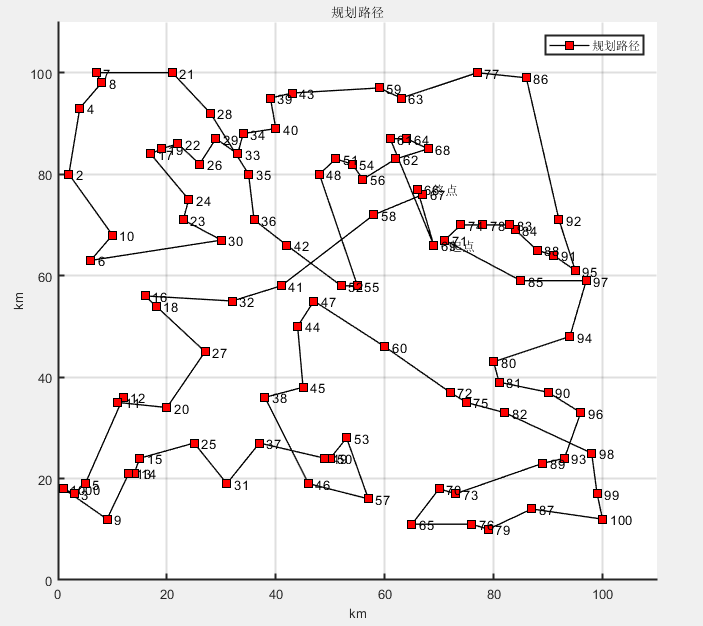
由于每次数据随机 不一致 所以 最终结果不稳定 可用固定的数据进行测试

最短距离:893.5288