1.定义
一棵二叉树由根结点、左子树和右子树三部分组成,若规定 D、L、R 分别代表遍历根结点、遍历左子树、遍历右子树,则二叉树的遍历方式有 6 种:DLR、DRL、LDR、LRD、RDL、RLD。由于先遍历左子树和先遍历右子树在算法设计上没有本质区别,所以,只讨论三种方式:
DLR根左右--前序遍历(根在前,从左往右,一棵树的根永远在左子树前面,左子树又永远在右子树前面 )
LDR左根右--中序遍历(根在中,从左往右,一棵树的左子树永远在根前面,根永远在右子树前面)
LRD左右根--后序遍历(根在后,从左往右,一棵树的左子树永远在右子树前面,右子树永远在根前面)
例如:
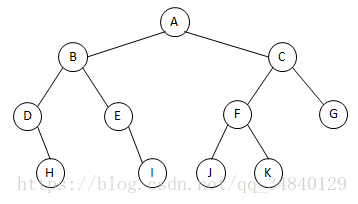
先(根)序遍历(根左右):A B D H E I C F J K G
中(根)序遍历(左根右) : D H B E I A J F K C G
后(根)序遍历(左右根) : H D I E B J K F G C A
2.程序实现
Python实现
#节点类 class node(): def __init__(self, value): self.value = value self.left = None self.right = None # 先序遍历 def preOrder(n): if n == None: return print(n.value, end=" ") preOrder(n.left) preOrder(n.right) # 中序遍历 def middleOrder(n): if n == None: return middleOrder(n.left) print(n.value, end=" ") middleOrder(n.right) # 后序遍历 def postOrder(n): if n == None: return postOrder(n.left) postOrder(n.right) print(n.value, end=" ") if __name__ == '__main__': a,b,c,d,e,f = node('a'),node('b'),node('c'),node('d'),node('e'),node('f') a.left = b a.right = e b.left = c b.right = d e.right = f preOrder(a) print() middleOrder(a) print() postOrder(a)
a
/
b e
/
c d f
输出
a b c d e f
c b d a e f
c d b f e a
C实现
typedef struct TreeNode { int data; TreeNode * left; TreeNode * right; TreeNode * parent; }TreeNode; void pre_order(TreeNode * Node)//前序遍历递归算法 { if(Node == NULL) return; printf("%d ", Node->data);//显示节点数据,可以更改为其他操作。在前面 pre_order(Node->left); pre_order(Node->right); } void middle_order(TreeNode *Node)//中序遍历递归算法 { if(Node == NULL) return; middle_order(Node->left); printf("%d ", Node->data);//在中间 middle_order(Node->right); } void post_order(TreeNode *Node)//后序遍历递归算法 { if(Node == NULL) return; post_order(Node->left); post_order(Node->right); printf("%d ", Node->data);//在最后 }
3.求二叉树结构
例题1:
已知某二叉树的前序遍历为A-B-D-F-G-H-I-E-C,中序遍历为F-D-H-G-I-B-E-A-C,请还原这颗二叉树。
解题思路:
从前序遍历中,我们确定了根结点为A,在从中序遍历中得出 F-D-H-G-I-B-E在根结点的左边,C在根结点的右边,那么我们就可以构建我们的二叉树的雏形。
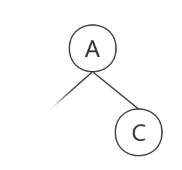
那么剩下的前序遍历为B-D-F-G-H-I-E,中序遍历为F-D-H-G-I-B-E, B就是我们新的“根结点”,从中序遍历中得出F-D-H-G-I在B的左边,E在B的右边,继续构建
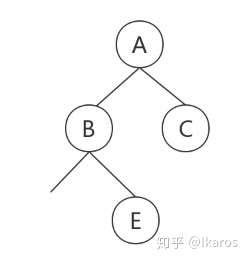
那么剩下的前序遍历为D-F-G-H-I,中序遍历为F-D-H-G-I,D就是我们新的“根结点”,从中序遍历中得出F在D的左边,H-G-I在D的右边,继续构建
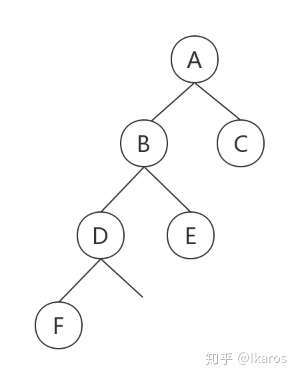
那么剩下的前序遍历为G-H-I,中序遍历为H-G-I,G就是我们新的“根结点”,从中序遍历中得出H在G的左边,I在G的右边,继续构建

例题2:
已知某二叉树的中序遍历为F-D-H-G-I-B-E-A-C,后序遍历为F-H-I-G-D-E-B-C-A,请还原这颗二叉树。
解题思路:
从后序遍历中,我们确定了根结点为A,在从中序遍历中得出 F-D-H-G-I-B-E 在根结点的左边,C在根结点的右边,那么我们就可以构建我们的二叉树的雏形。之后就是新根节点B,FDHGI在根左,E在根右。在之后就是新根D,F根左,HGI根右,然后就差不多了。
和前序和中序还原二叉树一样,我们同理可以通过中序和后序还原二叉树。
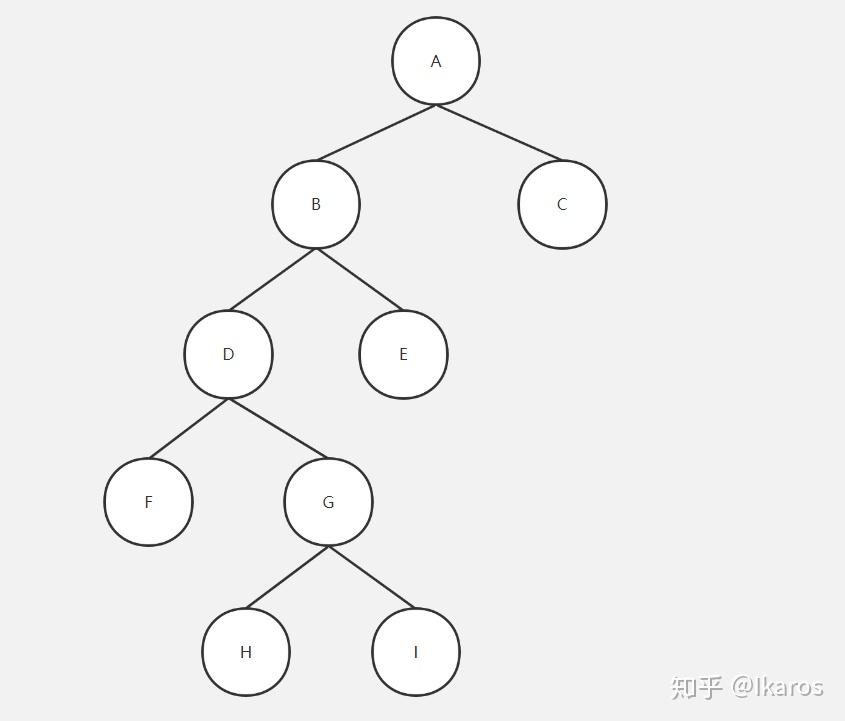
光有前序遍历和后序遍历是无法还原二叉树的。
4.BFS和DFS
BFS(广度优先遍历,Breadth First Search)及DFS(深度优先遍历,Depth First Search)是遍历树或图的两种最常用的方法。
参考
https://blog.csdn.net/u013834525/article/details/80421684
https://blog.csdn.net/qq_34840129/article/details/80619761
https://zhuanlan.zhihu.com/p/73438175
https://blog.csdn.net/Gene1994/article/details/85097507