P4009 汽车加油行驶问题
题目描述
给定一个(N×N)的方形网格,设其左上角为起点◎,坐标(1,1) ,(X)轴向右为正,(Y)轴向下为正,每个方格边长为1 ,如图所示。
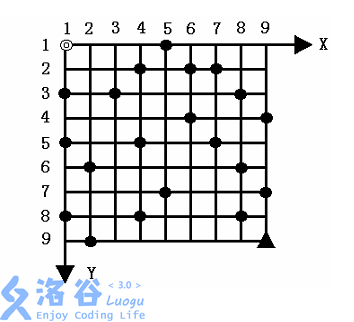
一辆汽车从起点◎出发驶向右下角终点▲,其坐标为((N,N)) 。
在若干个网格交叉点处,设置了油库,可供汽车在行驶途中加油。汽车在行驶过程中应遵守如下规则:
汽车只能沿网格边行驶,装满油后能行驶(K)条网格边。出发时汽车已装满油,在起点与终点处不设油库。
汽车经过一条网格边时,若其(X)坐标或(Y)坐标减小,则应付费用(B),否则免付费用。
汽车在行驶过程中遇油库则应加满油并付加油费用(A) 。
在需要时可在网格点处增设油库,并付增设油库费用(C)(不含加油费用(A))。
(N,K,A,B,C)均为正整数, 且满足约束: (2≤N≤100,2≤K≤10) 。
设计一个算法,求出汽车从起点出发到达终点所付的最小费用。
输入输出格式
输入格式:
文件的第一行是 (N,K,A,B,C)的值。
第二行起是一个 (N×N)的0-1方阵,每行(N)个值,至(N+1)行结束。
方阵的第(i)行第(j)列处的值为1表示在网格交叉点((i,j))处设置了一个油库,为(0)时表示未设油库。各行相邻两个数以空格分隔。
输出格式:
程序运行结束时,输出最小费用。
说明
(2≤n≤100,2≤k≤10)
据说是费用流,没看出来。连分层图都没看出来,胡乱打了个最短路偏分发现居然有强制消费。
分层图按(k)也就是走的步数来分层,但这里我打了优先队列BFS,本质上和disj最短路的思想是一样的,但似乎跑的慢一些??
Code:
#include <cstdio>
#include <queue>
#include <cstring>
#include <cstdlib>
using namespace std;
const int N=103;
const int I[5]={0,0,1,0,-1};
const int J[5]={0,1,0,-1,0};
int n,k,a,b,c;//方格大小,可连边长,加油费,倒车费,开厂费
int used[N][N][12],g[N][N],cost[5];
void init()
{
scanf("%d%d%d%d%d",&n,&k,&a,&b,&c);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%d",&g[i][j]);
cost[3]=cost[4]=b;
}
struct node
{
int i,j,w,dep;
node(){}
node(int i,int j,int w,int dep)
{
this->i=i;
this->j=j;
this->w=w;
this->dep=dep;
}
bool friend operator <(node n1,node n2)
{
return n1.w>n2.w;
}
};
priority_queue <node > q;
void work()
{
node t0(1,1,0,0);
q.push(t0);
while(!q.empty())
{
int ii=q.top().i,jj=q.top().j,dep=q.top().dep,w=q.top().w;
q.pop();
if(ii==n&&jj==n)
{
printf("%d
",w);
exit(0);
}
if(used[ii][jj][dep]) continue;
used[ii][jj][dep]=1;
for(int l=1;dep!=k&&l<=4;l++)
{
int i=ii+I[l],j=jj+J[l];
if(i>n||i<1||j>n||j<1) continue;
if(!g[i][j])
{
if(!used[i][j][dep+1])//直接走
{
node tt(i,j,w+cost[l],dep+1);
q.push(tt);
}
if(!used[i][j][0]&&i!=n&&j!=n)//开工厂
{
node tt(i,j,w+cost[l]+c+a,0);
q.push(tt);
}
}
if(g[i][j]&&!used[i][j][0])//强制消费
{
node tt(i,j,w+cost[l]+a,0);
q.push(tt);
}
}
}
}
int main()
{
init();
work();
return 0;
}
2018.7.5