You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Note: Given n will be a positive integer.
Example 1:
Input: 2 Output: 2 Explanation: There are two ways to climb to the top. 1. 1 step + 1 step 2. 2 steps
Example 2:
Input: 3 Output: 3 Explanation: There are three ways to climb to the top. 1. 1 step + 1 step + 1 step 2. 1 step + 2 steps 3. 2 steps + 1 step
斐波那契数列,没啥说的,可以DP或者简单的迭代求解!
class Solution(object): def climbStairs(self, n): """ :type n: int :rtype: int """ # fib a = b = 1 for i in xrange(2, n+1): a, b = b+a, a return a
DP:
class Solution(object):
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
# fib
ways = [1]*(n+1)
for i in xrange(2, n+1):
ways[i] = ways[i-2]+ways[i-1]
return ways[n]
还可以使用数学知识求解:
This is Fibonacci number, and the world has already worked out an formula that
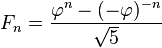
and where
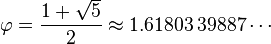
or you can check the wiki Fibonacci Number
and noticed the Fibonacci begins with F(0)=0, F(1)=1, F(2)=1, F(3)=2
but this problem begins with F’(1)=1, F’(2)=2
So we need a (n++) at the beginning to match the Fibonacci formula
int climbStairs(int n) {
n++;
double root5 = pow(5, 0.5);
double result = 1/root5*( pow((1+root5)/2, n) - pow((1-root5)/2, n) );
return (int)(result);
}