2011年,C语言老师给我们讲冒泡排序。
2014年,听同学说起他面试时和面试官提起冒泡排序。
2015年,大学本科刚毕业,开始找工作,我还记得我在笔记中写了冒泡排序的代码,结果还真的被问到了。
2019年,公司首席架构师跟我提到冒泡排序。
什么是冒泡排序呢?
冒泡排序,Bubble Sort,通过依次来比较相邻两个元素的大小,在每一次的比较的过程中,两个元素,通过交换来达到有序的目的。
- 如果一组无序的数列想要从小到大排序,那么两个元素比较,通过交换来实现,左边的元素要比右边的元素要小。
- 如果一组无序的数列想要从大到小排序,那么两个元素比较,通过交换来实现,左边的元素要比右边的元素要大。
就像碳酸饮料中的气泡一样,从底部一直冒泡到顶部。
我想通过一组数据来阐述冒泡排序的过程。
- 准备一组无序的数列,从小到大依次排序。

- 开始排序开始。由于6>3,因此两个元素交换。

- 由于6>2,因此两个元素交换。

- 由于6>1,因此两个元素交换。

- 由于6<8,因此两个元素不交换。
- 由于8<9,因此两个元素不交换。
- 由于9>7,因此两个元素交换。

- 由于9>5,因此两个元素交换。

- 第一轮排序结束。此时,元素9处于有序区域。

- 第二轮排序开始。由于3>2。因此两个元素交换。

- 由于3>1。因此两个元素交换。

- 由于3<6。因此两个元素不交换。
- 由于6<8。因此两个元素不交换。
- 由于8>7。因此两个元素交换。

- 由于8>5。因此两个元素交换。

- 由于8<9。因此两个元素不交换。
- 第二轮排序结束。此时,元素8和9处于有序区域。

- 第三轮排序开始。由于2>1。因此两个元素交换。

- 由于2<3。因此两个元素不交换。
- 由于3<6。因此两个元素不交换。
- 由于6<7。因此两个元素不交换。
- 由于7>5,因此两个元素交换。

- 第三轮排序结束。此时,元素7,8和9处于有序区域。

- 第四轮排序开始。由于1<2。因此两个元素不交换。
- 由于2<3。因此两个元素不交换。
- 由于3<6。因此两个元素不交换。
- 由于6>5。因此两个元素交换。

- 第四轮排序结束。此时,元素6,7,8,9在有序区域内。

- 第五轮排序开始。由于1<2。因此两个元素不交换。
- 由于2<3。因此两个元素不交换。
- 由于3<5。因此两个元素不交换。
- 第五轮排序结束。此时,元素5,6,7,8,9在有序区域内。
- 第六轮排序开始。由于1<2。因此两个元素不交换。
- 由于2<3。因此两个元素不交换。
- 第六轮排序结束。此时,元素3,5,6,7,8,9在有序区域内。
- 第七轮排序开始。由于1<2。因此两个元素不交换。
- 第七轮排序结束。此时,元素2,3,5,6,7,8,9在有序区域内。
- 第八轮排序开始。
- 第八轮排序结束。此时,元素1,2,3,5,6,7,8,9在有序区域内。可见最后一轮没有必要存在。
最后我们使用Java代码来展示上述的算法。
1 private static void sort() { 2 3 Integer[] data = {6,3,2,1,8,9,7,5}; 4 5 for(int i=0; i<data.length-1; i++) { 6 7 for(int j=0; j<data.length-i-1; j++) { 8 9 if(data[j] > data[j+1]) { 10 int k = data[j]; 11 data[j] = data[j+1]; 12 data[j+1] = k; 13 } 14 15 } 16 } 17 18 }
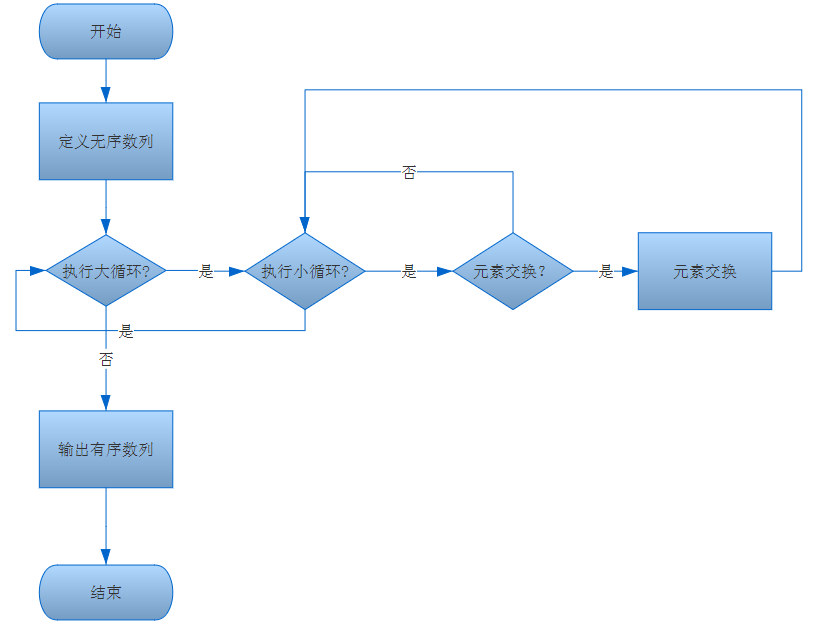
从上述的代码以及流程图中。大致的步骤如下:
- 定义一组无序数列。
- 第一层循环。第一层循环的次数是(元素个数-1)。
- 第二层循环。第二层循环的次数是无序区域内,元素1和元素2,元素2和元素3...依次两两比较。
- 两个元素比较,根据规则确认元素是否需要交换。
- 继续第二步。直到循环的次数 = (元素个数-1),结束循环,输出有序数列,结束。
从以上的现象来看,我们得出结论和思考:
- 排序的轮数等于元素的个数-1。是否可以较少轮数,上述的例子中实际上在完成第四轮以后已经是一组有序的数列。从上述代码来看,第5行控制的是轮数,而第7行是每一轮中无序区域中元素的两两比较。从本质上来说,我们需要在发现没有元素交换的情况下,就能够说明已经有序,我们需要尽早在21行结束。代码如下所示:
1 private static void sort() { 2 3 Integer[] data = {6,3,2,1,8,9,7,5}; 4 5 for(int i=0; i<data.length-1; i++) { 6 7 boolean isSorted = true; 8 9 for(int j=0; j<data.length-i-1; j++) { 10 11 if(data[j] > data[j+1]) { 12 int k = data[j]; 13 data[j] = data[j+1]; 14 data[j+1] = k; 15 16 isSorted = false; 17 } 18 } 19 20 if(isSorted) { 21 break; 22 } 23 } 24 25 }
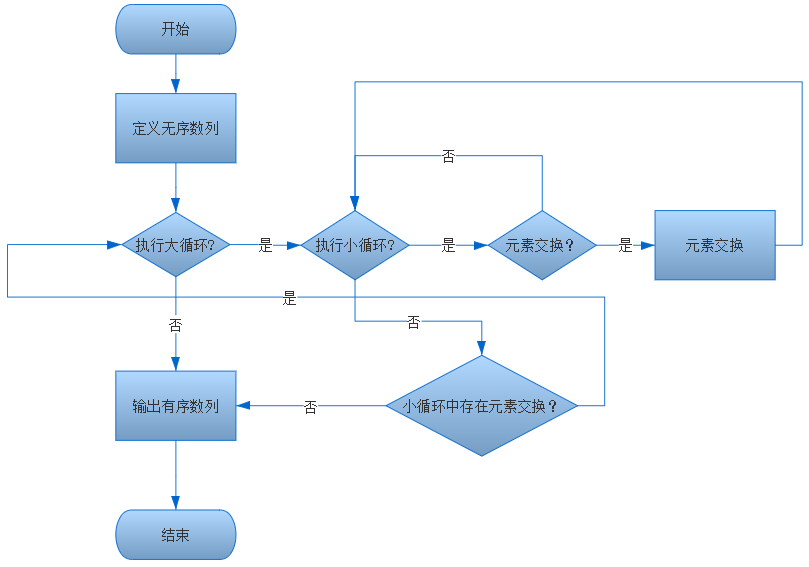
从上述的代码和流程图中,如果在第一层的循环中第二次始终没有元素交换,表明数列已经有序,直接输出。
- 完成每一轮,有序区域的元素个数增加1。是否可以冲破每一次有序区域只能增加1的僵局?我们采取在一个大的轮询中,记录最后交换的元素的下标,把这个下标作为无序区域的边界,用来最大提高有序区域元素数量增加的加速度。
1 private static void sort() { 2 3 Integer[] data = {6,3,2,1,8,9,7,5}; 4 5 //最后交换的元素的下标 6 int lastIndexOfSwap = 0; 7 //无序数列边界元素的下标 8 int borderIndexOfUnsort = data.length - 1; 9 10 for(int i=0; i<data.length-1; i++) { 11 12 boolean isSorted = true; 13 14 for(int j=0; j<borderIndexOfUnsort; j++) { 15 16 if(data[j] > data[j+1]) { 17 int k = data[j]; 18 data[j] = data[j+1]; 19 data[j+1] = k; 20 21 isSorted = false; 22 23 lastIndexOfSwap = j; 24 } 25 } 26 27 borderIndexOfUnsort = lastIndexOfSwap; 28 29 if(isSorted) { 30 break; 31 } 32 33 } 34 35 }
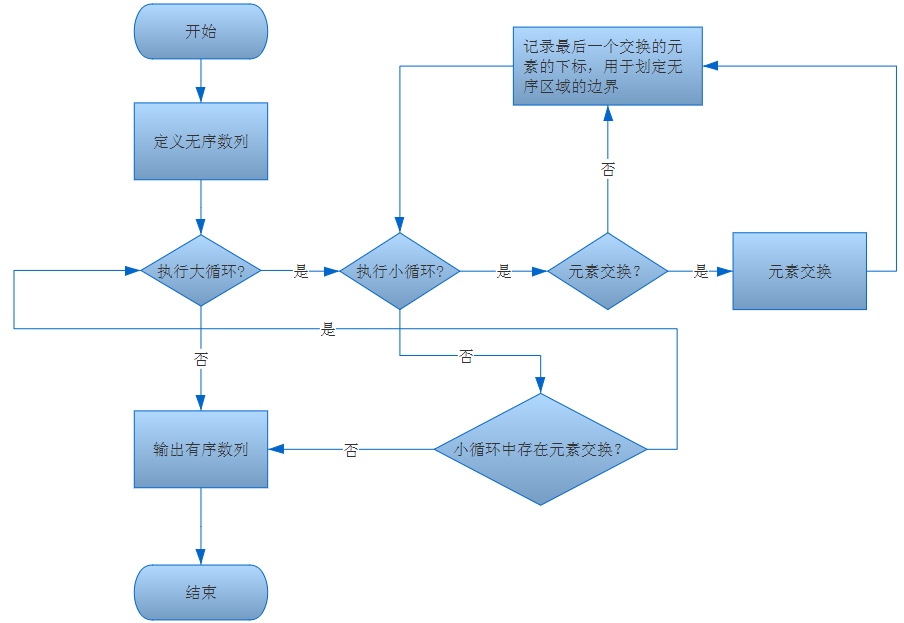
冒泡排序是最简单的一种排序算法,3个版本演进,也许并没有提高多大的效能,更多应该是对于算法的思维。