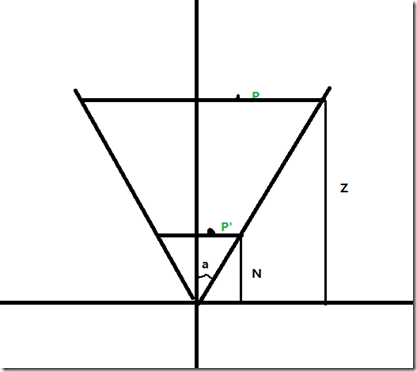
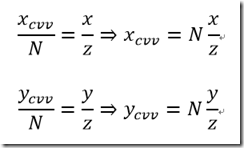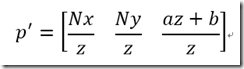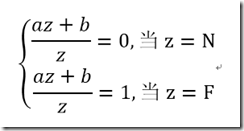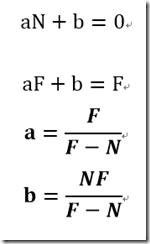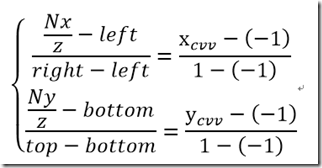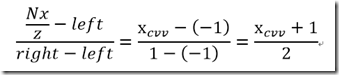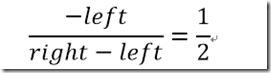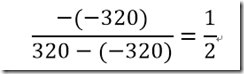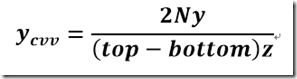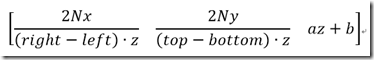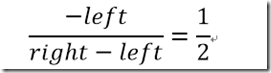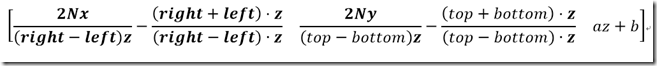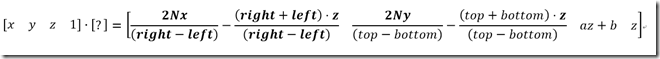图一
透视矩阵把物体投影到一个距离摄像机为N的一个平面上,用图一可以看,我们把P投影近裁剪面P’点
我们定义两个点
根据相似三角形原理我们得到公式1
那么
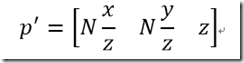 因为z值永远都是N,但是我们可以用来存储一些其他信息,比如原来的Z值
因为z值永远都是N,但是我们可以用来存储一些其他信息,比如原来的Z值
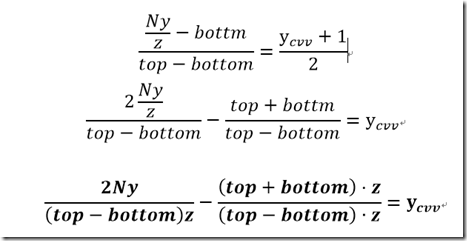
换种写法
用齐次坐标系表达的话
那么我们根据P P’推导下投影矩阵
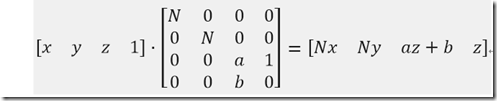
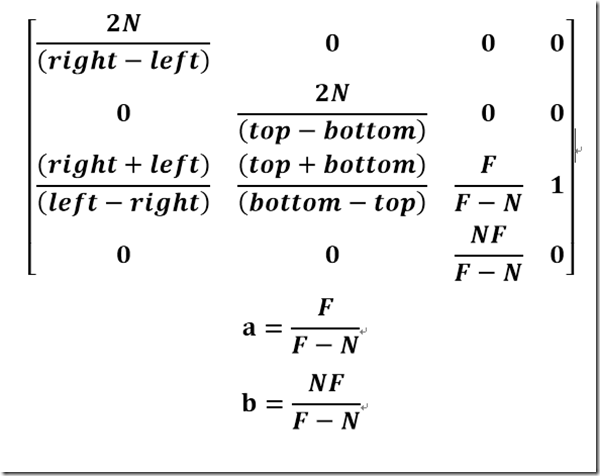
得到投影矩阵
到这里我们 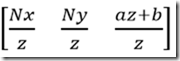 。经过除以齐次坐标得到真正的投影空间坐标。一般透视矩阵让人难于理解是因为,他还把其他一步功能糅杂在里面,把两步操作隐藏在一个矩阵中。
。经过除以齐次坐标得到真正的投影空间坐标。一般透视矩阵让人难于理解是因为,他还把其他一步功能糅杂在里面,把两步操作隐藏在一个矩阵中。
我们知道Camera可是区域是个梯形椎体,在计算中,对于计算机的椎体的裁决(裁剪掉摄像机外围的不可见点)计算比较复杂。我们如何使裁剪变的更容易呢。如果所有的都变换的一个规正的形状中就比较好了,比如说一个立方体或者一个长方体中。这样就比较好判断。只要根据长宽高比值比较就可以判断是否在摄像机的中,如果不在就剔除掉。所以在透视矩阵是分为两步 透视乘法变换,变换到canonical view volume(CVV)规则观察体。在中间还有一步是CVV裁剪。后面再进行透视除法,得到真正的投影点
。我们今天只讨论透视乘法和透视除法两步。我们这里先讨论DX情况下CVV空间,OpenGL参数有些差异。等下说明,原理一样
我们在先在DX情况下讨论。
先说下Z轴,Z轴在[0,1]我们定义近的裁剪面距离为N,远的裁剪面距离为F,
变换得到
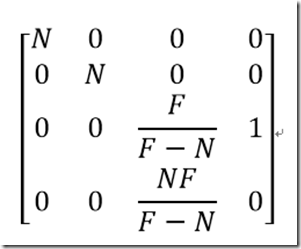
那么投影矩阵现在可以写成
现在计算X轴和Y轴 x在[-1,1] y[-1,1],定义屏幕左右边界为 right和left 屏幕上下边界为 top和bottom
先计算X轴的情况
我们这里分为两种情况,一种是特殊,一种是普通
特殊情况是 right left 大小相同 一正一负,投影点正好在屏幕中心点
另一个通用的是左右两边不对称。投影点不在屏幕中心点
我们先讨论特殊情况,也是我们一般碰到的,屏幕的中心在投影点,左右对称
那么上面公式可以变换成
我们可以发现在公式中
定义屏幕宽是640分辨率,中心是0 右边是-320 左边是 320
得到
同样
现在的投影点p'写成
那么我们根据P P’推导下投影矩阵
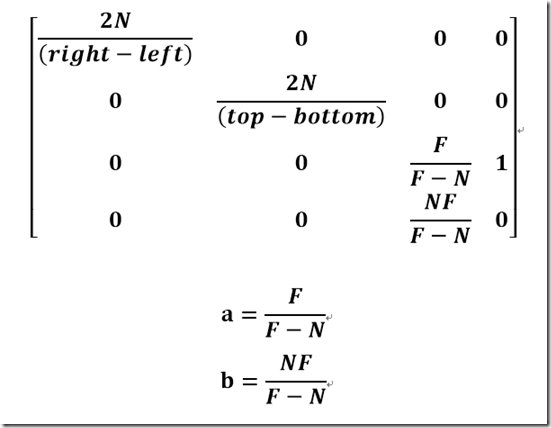
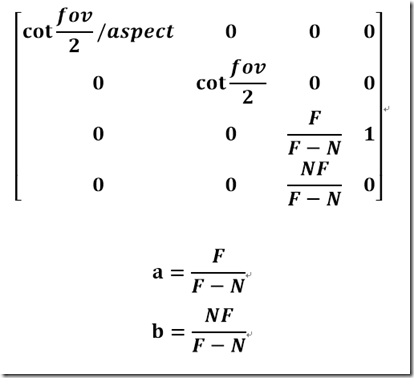
那么现在的投影矩阵是
这个就是我们推导的投影矩阵了,我们同样跟MSDN的
D3DXMatrixPerspectiveLH
https://msdn.microsoft.com/en-us/library/windows/desktop/bb205352(v=vs.85).aspx
投影矩阵比对下
发现是一样的,证明推导没错。
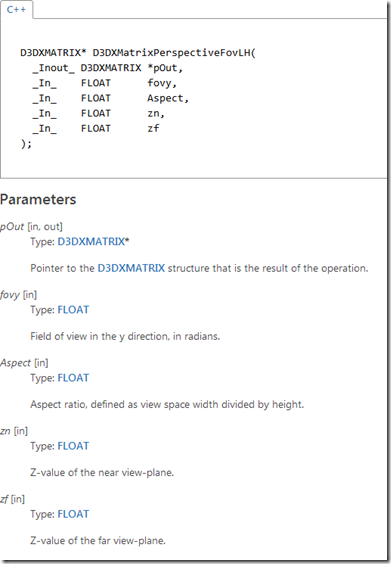
MSDN里面还有种写法是传入参数 屏幕的宽高比 和 镜头视角大小
D3DXMatrixPerspectiveFovLH
https://msdn.microsoft.com/en-us/library/windows/desktop/bb205350(v=vs.85).aspx
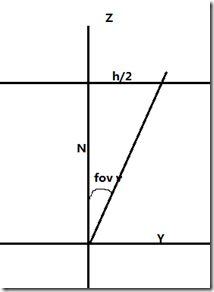
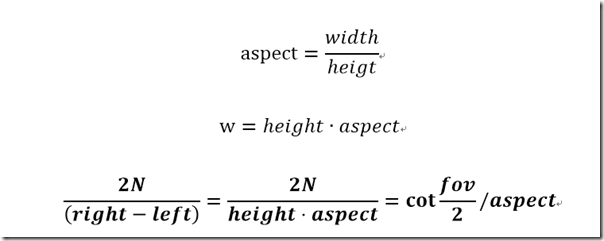
这里镜头视角是取Y-Z平面的视角大小,我们也可以用X-Y平面看推导出来。但是推导出投影矩阵的有差异
如图根据三角函数我们可以推导出以下公式
那么矩阵中 元素我们可以换种写法
根据宽高比
那么投影矩阵可以写成
我们跟MSDN里面的对比下是一样的
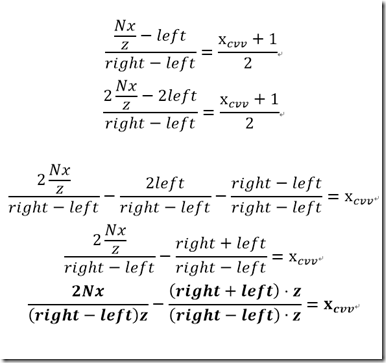
继续我们刚刚讨论 屏幕中心不在投影点的情况,那么就没有消除
同样
现在P'的写法
反推导矩阵
MSDN里面
D3DXMatrixPerspectiveOffCenterLH
https://msdn.microsoft.com/en-us/library/windows/desktop/bb205353(v=vs.85).aspx
就是这种推导,比对下
当我们屏幕中心在投影点的时候 Left+Right = 0 Top+Bottom =0 ,代入,其实和特殊矩阵是一样的
OpenGL 待续